BZOJ2539 Spoj 10707 Count on a tree II
阿新 • • 發佈:2019-02-03
roo lca tor 情況 getchar() 連續 http bzoj clas
題面
題解
如果不強制在線,這道題目是樹上莫隊練手題
我們知道莫隊是離線的,但是萬一強制在線就涼涼了
於是我們就需要一些操作:樹分塊
看到這個圖:
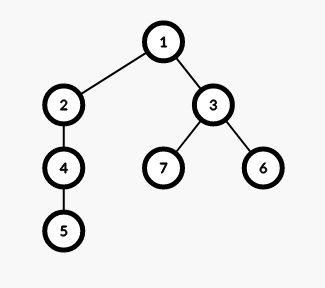
這裏有\(7\)個點,我們每隔\(2\)深度分塊
但是我們要保證分塊的連續性,於是分成了\((1,2)(7,6,3)(4,5)\)三塊
現在給了你兩個將詢問的點\(u,v(dep[u]>dep[v])\),分類討論:
兩個點在同一個塊內
直接暴力
兩個點不在同一個塊內
這種情況比較復雜,記一個塊的根為\(rt[i]\),則它到另外所有點的答案我們可以很輕松地
統計出來,只需要對於每個\(rt[i]\)暴力統計一遍就可以了。那麽現在我們要考慮的只有\(u\)
到它的塊的根\(x\)路徑上是否會對答案產生貢獻:
對於這個,我們可以將這個分塊可持久化,維護這個點的顏色在它的祖先中出現最深的位置
的深度,那麽一個塊只需繼承上面的塊,並將在這個塊中顏色的答案更新,因為那個顏色如
果出現在這個位置,那麽答案肯定更優。有了上面的鋪墊,那我們只需對\(u\to x\)上的點暴力算它的深度是否超過\(\mathrm{LCA}(u, v)\)即可
代碼
#include<cstdio> #include<cstring> #include<cctype> #include<cmath> #include<algorithm> #define RG register #define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout) #define clear(x, y) memset(x, y, sizeof(x)) inline int read() { int data = 0, w = 1; char ch = getchar(); while(ch != '-' && (!isdigit(ch))) ch = getchar(); if(ch == '-') w = -1, ch = getchar(); while(isdigit(ch)) data = data * 10 + (ch ^ 48), ch = getchar(); return data * w; } const int maxn(40010), SQRT(210); struct edge { int next, to; } e[maxn << 1]; int head[maxn], e_num; inline void add_edge(int from, int to) { e[++e_num] = (edge) {head[from], to}; head[from] = e_num; } int n, m, Len, a[maxn], b[maxn], _a[maxn], r[maxn]; int P[maxn][SQRT], A[SQRT][maxn], fa[maxn], dep[maxn]; int q[maxn], belong[maxn], top, cnt, SIZE, root[maxn]; int c[maxn], Ans; struct Block { int a[SQRT]; void insert(const Block&, int, int); int &operator [] (const int &x) { return P[a[b[x]]][r[x]]; } const int &operator [] (const int &x) const { return P[a[b[x]]][r[x]]; } } s[maxn]; void Block::insert(const Block &rhs, int x, int d) { int blk = b[x], t = r[x]; memcpy(a, rhs.a, sizeof(a)); memcpy(P[++SIZE], P[a[blk]], sizeof(P[0])); P[a[blk] = SIZE][t] = d; } namespace Tree { int belong[maxn], heavy[maxn], size[maxn]; void dfs(int x, int chain) { belong[x] = chain; if(!heavy[x]) return; dfs(heavy[x], chain); for(RG int i = head[x]; i; i = e[i].next) { int to = e[i].to; if(to == fa[x] || to == heavy[x]) continue; dfs(to, to); } } int LCA(int x, int y) { while(belong[x] != belong[y]) { if(x[belong][dep] < y[belong][dep]) std::swap(x, y); x = x[belong][fa]; } return dep[x] < dep[y] ? x : y; } } int dfs(int x, int f) { using Tree::size; using Tree::heavy; fa[x] = f, size[x] = 1; s[x].insert(s[f], a[x], dep[x] = dep[f] + 1); q[++top] = x; int maxd = dep[x], p = top; for(RG int i = head[x]; i; i = e[i].next) { int to = e[i].to; if(to == f) continue; maxd = std::max(maxd, dfs(to, x)); size[x] += size[to]; if(size[heavy[x]] < size[to]) heavy[x] = to; } if(maxd - dep[x] >= Len || p == 1) { root[++cnt] = x; for(RG int i = p; i <= top; i++) belong[q[i]] = cnt; top = p - 1; return dep[x] - 1; } return maxd; } void Pre(int x, int f, int *s) { if(!c[a[x]]++) ++Ans; s[x] = Ans; for(RG int i = head[x]; i; i = e[i].next) if(e[i].to != f) Pre(e[i].to, x, s); if(!--c[a[x]]) --Ans; } int Solve1(int x, int y) { for(top = Ans = 0; x != y; x = fa[x]) { if(dep[x] < dep[y]) std::swap(x, y); if(!c[q[++top] = a[x]]) c[a[x]] = 1, ++Ans; } for(Ans += !c[a[x]]; top;) c[q[top--]] = 0; return Ans; } int Solve2(int x, int y) { if(dep[root[belong[x]]] < dep[root[belong[y]]]) std::swap(x, y); int x1 = root[belong[x]], d = dep[Tree::LCA(x, y)]; Ans = A[belong[x]][y]; for(top = 0; x != x1; x = fa[x]) if(!c[a[x]] && s[x1][a[x]] < d && s[y][a[x]] < d) c[q[++top] = a[x]] = 1, ++Ans; while(top) c[q[top--]] = 0; return Ans; } int main() { #ifndef ONLINE_JUDGE freopen("cpp.in", "r", stdin); #endif n = read(), m = read(), Len = sqrt(n) - 1; for(RG int i = 1; i <= n; i++) b[i] = (i - 1) / Len + 1, r[i] = i % Len; for(RG int i = 1; i <= n; i++) a[i] = _a[i] = read(); std::sort(_a + 1, _a + n + 1); int tot = std::unique(_a + 1, _a + n + 1) - _a - 1; for(RG int i = 1; i <= n; i++) a[i] = std::lower_bound(_a + 1, _a + tot + 1, a[i]) - _a; for(RG int i = 1, x, y; i < n; i++) x = read(), y = read(), add_edge(x, y), add_edge(y, x); top = 0, dfs(1, 0), Tree::dfs(1, 1); for(RG int i = 1; i <= cnt; i++) Pre(root[i], 0, A[i]); int ans = 0; while(m--) { int x = ans ^ read(), y = read(); printf("%d\n", ans = (belong[x] == belong[y] ? Solve1(x, y) : Solve2(x, y))); } return 0; }
BZOJ2539 Spoj 10707 Count on a tree II
