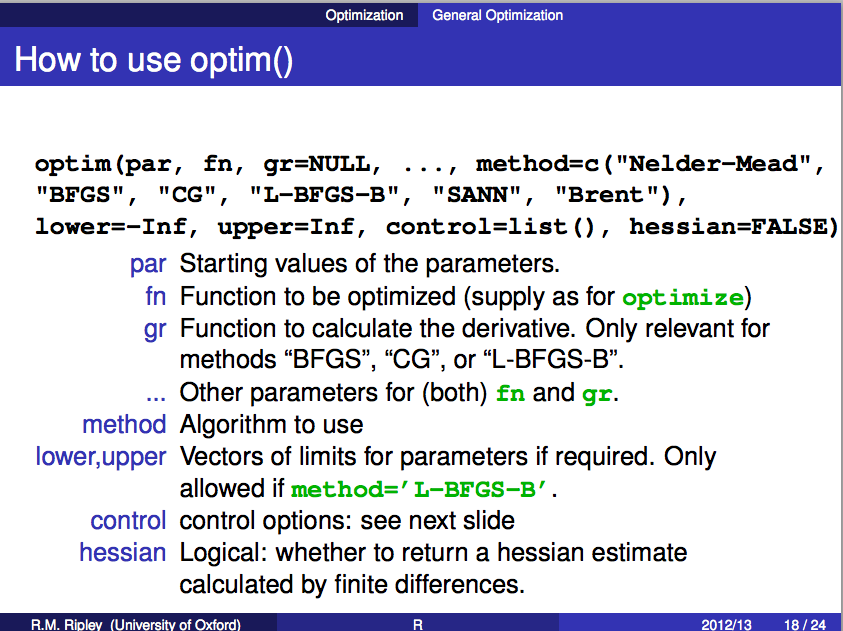
R語言包_stats::optim
stats中的optim函式是解決優化問題的一個簡易的方法。
Univariate Optimization
f = function(x,a) (x-a)^2
xmin = optimize(f,interval = c(0,1),a=1/3)
xminGeneral Optimization
optim函式包含了幾種不同的演算法。
演算法的選擇依賴於求解導數的難易程度,通常最好提供原函式的導數。
在求解之前,一般需要scale。
可以嘗試用不同的方法求解同樣的問題。
Nelder-Mead method
optim預設的方法。
又稱下山單純形法,可做非線性函式的極值以及曲線擬合。
其主要思想是:
在n維空間構建(n+1)頂點的多面體,通過reflection,expansion,contraction,來逐步逼近最佳點
特點是:
1. 不適用函式的導數資訊
2. 對不可導函式適用
3. 可能很慢
BFGS method
屬於quasi-Newton方法。
首先,簡單介紹牛頓法:
牛頓法基於目標函式的二階導數(海森矩陣),收斂速度快,迭代次數少,尤其在最優值附近,收斂速度是二次的。
缺點是:海森矩陣稠密時,每次迭代計算量交大,且每次都會重新計算目標函式的海森矩陣的逆。這樣以來,問題規模大時,其計算量以及儲存空間都很大。
擬牛頓法是在牛頓法基礎上的改進,其引入了海森矩陣的近似矩陣,避免了每次迭代都需要計算海森矩陣的逆,其收斂速度介於梯度下降和牛頓法之間,屬於超線性。
同時,牛頓法在每次迭代時不能保證海森矩陣總是正定的,一旦其不是正定,優化方向就會跑偏,從而使牛頓法失效,也證明了牛頓法的魯棒性較差。
擬牛頓法利用海森矩陣的逆矩陣代替海森矩陣,雖然每次迭代不一定保證最優化的方向,但是近似矩陣始終正定,因此演算法總是朝著最優值搜尋。
注意:
1. 使用函式導數資訊,通過人工提供或者有限微分
2. 高維的資料儲存會很大
CG method
一種共軛梯度法(conjugate gradient),選擇連續的、與橢圓軸線相仿的路徑。
特點:
1. 不儲存海森矩陣
2. 三種不同的路徑搜尋方法
3. 與BFGS相比,較差的魯棒性
4. 使用函式導數資訊
L-BFGS-B method
A limited memory version of BFGS
特點:
1. 不儲存海森矩陣,只有一個對海森矩陣大小受限的更新步驟。
2. 使用導數資訊
3. 可以把解決方法限制到box裡,是optim中僅有的方法。
SANN method
模擬退火法(simulated annealing)的變種。
特點:
1. 隨機演算法
2. 接受以正概率提升目標的改變
3. 不使用導數資訊
4. 收斂很慢,但是找到一個good solution很快
Brent method
An interface to optimize
特點:
1. 僅適用於一維問題
2. 可以在其他函式中包含
How to use
optim
control options
components of returned value
constrained optimization
Exampels
One Dimensional Ex1
假定
其導數為
# we supply negative f, since we want to maximize.
f <- function(x) -exp(-( (x-2)^2 ))
######### without derivative
# I am using 1 at the initial value
# $par extracts only the argmax and nothing else
optim(1, f)$par
######### with derivative
df <- function(x) -2*(x-2)*f(x)
optim(1, f, df, method="CG")$par
######### with "Brent" method
optim(1,f,method="Brent",lower=-0,upper=3)$par
# figure
x = seq(0,3,length.out = 100)
y = f(x)
plot(x,y)One Dimensional Ex2
假定
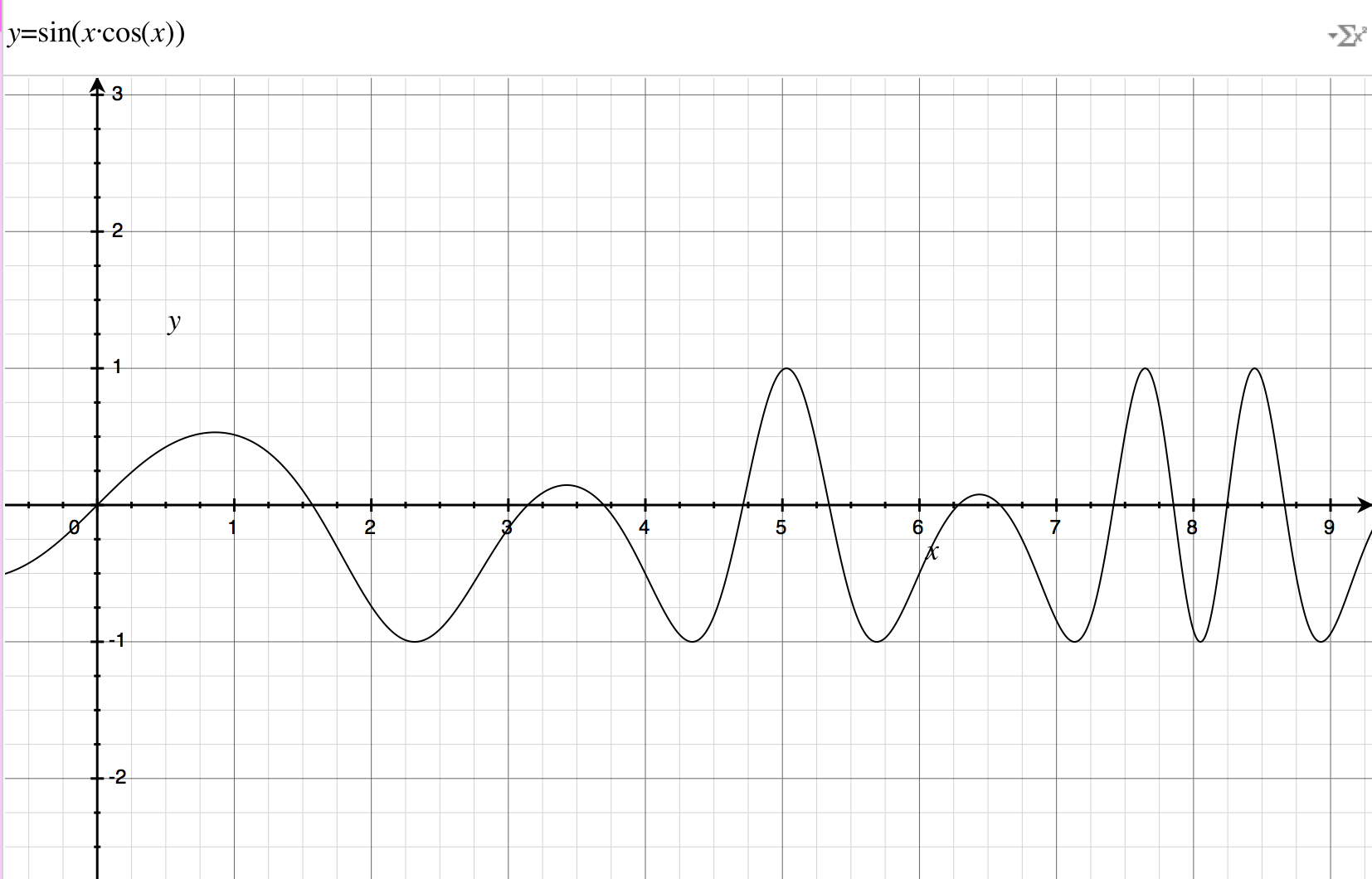
#演算法可以很快地發現與初值相近的區域性最優值。
f <- function(x) sin(x*cos(x))
optim(2, f)$par
optim(4, f)$par
optim(6, f)$par
optim(8, f)$par
Two Dimensional Ex3
Rosenbrock function:
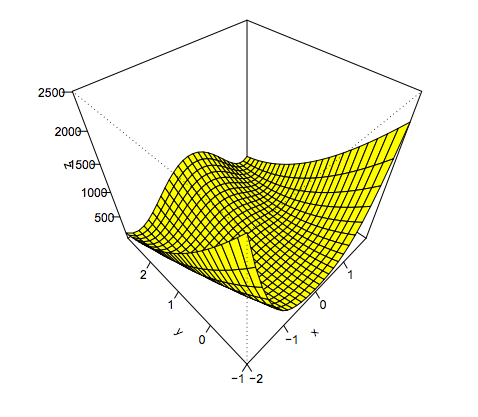
This function is strictly positive, but is 0 when y = x^2, and x = 1, so (1, 1) is a minimum.
Let’s see if optim can figure this out. When using optim for multidimensional optimization, the input in your function definition must be a single vector.
# 繪圖
f <- function(x1,y1) (1-x1)^2 + 100*(y1 - x1^2)^2
x <- seq(-2,2,by=.15)
y <- seq(-1,3,by=.15)
z <- outer(x,y,f)
persp(x,y,z,phi=45,theta=-45,col="yellow",shade=.00000001,ticktype="detailed")
# 求解
f <- function(x) (1-x[1])^2 + 100*(x[2]-x[1]^2)^2
# starting values must be a vector now
optim( c(0,0), f )$par
[1] 0.9999564 0.9999085Two Dimensional Ex4
Himmelblau’s function:
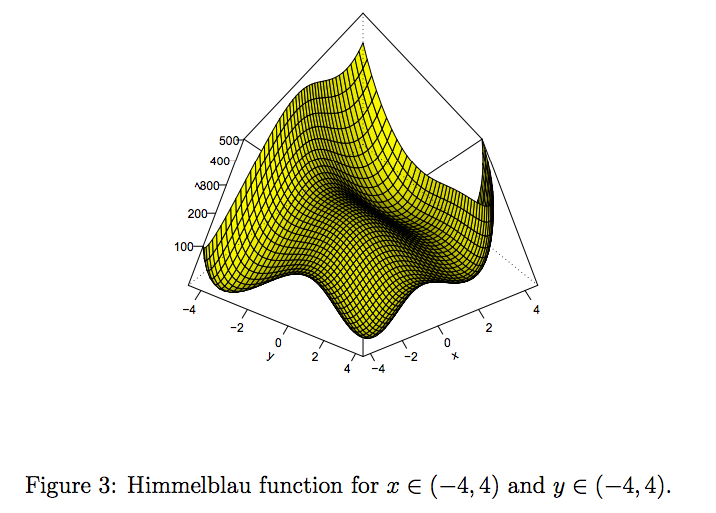
There appear to be four “bumps” that look like minimums in the realm of (-4,-4), (2,-2),(2,2) and (-4,4).
Again this function is strictly positive so the function is minimized when x^2 + y − 11 = 0 and x + y^2 − 7 = 0.
#畫圖
f <- function(x1,y1) (x1^2 + y1 - 11)^2 + (x1 + y1^2 - 7)^2
x <- seq(-4.5,4.5,by=.2)
y <- seq(-4.5,4.5,by=.2)
z <- outer(x,y,f)
persp(x,y,z,phi=-45,theta=45,col="yellow",shade=.65 ,ticktype="detailed")
#求解區域性最優值
f <- function(x) (x[1]^2 + x[2] - 11)^2 + (x[1] + x[2]^2 - 7)^2
optim(c(-4,-4),f)$par
optim(c(2,-2), f)$par
optim(c(2,2), f)$par
optim(c(-4,4),f)$par
#which are indeed the true minimums. This can be checked by seeing that these inputs
correspond to function values that are about 0.Fit a probit regression model
pass
Minimise residual sum of squares
# 初始化資料
d = data_frame(x=1:6,y=c(1,3,5,6,8,12))
d
ggplot(d,aes(x,y)) + geom_point() + stat_smooth(method = "lm")
# 最小問題的優化函式
min.RSS = function(data,par) {
with(data,sum((par[1]+par[2]*x-y)^2))
}
#optim函式呼叫的格式
result = optim(par=c(0,0),min.RSS,data=d)
#optim呼叫的結果引數
result$par
result$value
result$counts
result$convergence
result$message
#視覺化分析結果
ggplot(d,aes(x,y)) + geom_point() +geom_abline(intercept=result$par[1],
slope=result$par[2],color="red")
#optim與lm的結果對比分析
lm(y~x,data=d)
result$par
Maximum likelihood
To fit a Poisson distribution to x I don’t minimise the residual sum of squares, instead I maximise the likelihood for the chosen parameter lambda.
# 觀測資料
obs = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 17, 42, 43)
freq = c(1392, 1711, 914, 468, 306, 192, 96, 56, 35, 17, 15, 6, 2, 2, 1, 1)
x <- rep(obs, freq)
plot(table(x), main="Count data")
qplot(x,stat_bin=1)
# 優化函式,注意“-”號
lklh.poisson <- function(x, lambda) lambda^x/factorial(x) * exp(-lambda)
log.lklh.poisson <- function(x, lambda){
-sum(x * log(lambda) - log(factorial(x)) - lambda)
}
# 呼叫optim
optim(par=2,log.lklh.poisson,x=x)
optim(par=2,log.lklh.poisson,x=x,method="Brent",lower=2,upper=3)
# 比較結果
library(MASS)
fitdistr(x, "Poisson")
mean(x)
# 系統資訊
sessionInfo()