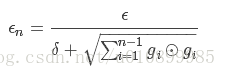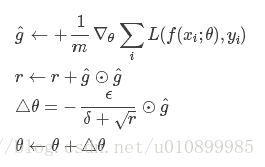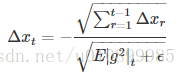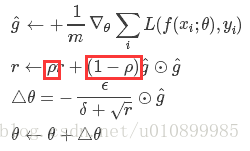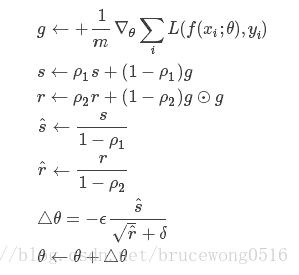深度學習最全優化方法總結比較及在tensorflow實現
梯度下降演算法針對凸優化問題原則上是可以收斂到全域性最優的,因為此時只有唯一的區域性最優點。而實際上深度學習模型是一個複雜的非線性結構,一般屬於非凸問題,這意味著存在很多區域性最優點(鞍點),採用梯度下降演算法可能會陷入區域性最優,這應該是最頭疼的問題。這點和進化演算法如遺傳演算法很類似,都無法保證收斂到全域性最優。因此,我們註定在這個問題上成為“高階煉丹師”。可以看到,梯度下降演算法中一個重要的引數是學習速率,適當的學習速率很重要:學習速率過小時收斂速度慢,而過大時導致訓練震盪,而且可能會發散。理想的梯度下降演算法要滿足兩點:收斂速度要快;能全域性收斂。為了這個理想,出現了很多經典梯度下降演算法的變種,下面將分別介紹它們。
SGD
梯度下降演算法(Gradient Descent Optimization)是神經網路模型訓練最常用的優化演算法。梯度下降演算法背後的原理:目標函式J(θ)關於引數θ的梯度將是目標函式上升最快的方向,對於最小化優化問題,只需要將引數沿著梯度相反的方向前進一個步長(學習速率),就可以實現目標函式的下降。引數更新公式如下:
其中是引數的梯度。
根據計算目標函式J(θ)採用資料量的大小,梯度下降演算法又可以分為批量梯度下降演算法(Batch Gradient Descent),隨機梯度下降演算法(Stochastic GradientDescent)和小批量梯度下降演算法(Mini-batch Gradient Descent)
- 批量梯度下降演算法,J(θ)是在整個訓練集上計算的,如果資料集比較大,可能會面臨記憶體不足問題,而且其收斂速度一般比較慢。
- 隨機梯度下降演算法,J(θ)是針對訓練集中的一個訓練樣本計算的,又稱為線上學習,即得到了一個樣本,就可以執行一次引數更新。所以其收斂速度會快一些,但是有可能出現目標函式值震盪現象,因為高頻率的引數更新導致了高方差。
- 小批量梯度下降演算法,是折中方案,J(θ)選取訓練集中一個小批量樣本計算,這樣可以保證訓練過程更穩定,而且採用批量訓練方法也可以利用矩陣計算的優勢。這是目前最常用的梯度下降演算法。
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(loss)
momentum
SGD方法的一個缺點是,其更新方向完全依賴於當前的batch,因而其更新十分不穩定,每次迭代計算的梯度含有比較大的噪音。解決這一問題的一個簡單的做法便是引入momentum,momentum即動量,是BorisPolyak在1964年提出的,其基於物體運動時的慣性:將一個小球從山頂滾下,其初始速率很慢,但在加速度作用下速率很快增加,並最終由於阻力的存在達到一個穩定速率,即更新的時候在一定程度上保留之前更新的方向,同時利用 當前batch的梯度 微調最終的更新方向。這樣一來,可以在一定程度上增加穩定性,從而學習地更快,並且還有一定擺脫區域性最優的能力。
其更新方程如下:
可以看到,引數更新時不僅考慮當前梯度值,而且加上了一個動量項γm,但多了一個超參γ,通常γ設定為0.5,直到初始學習穩定,然後增加到0.9或更高。相比原始梯度下降演算法,動量梯度下降演算法有助於加速收斂。當梯度與動量方向一致時,動量項會增加,而相反時,動量項減少,因此動量梯度下降演算法可以減少訓練的震盪過程。
tf.train.MomentumOptimizer(learning_rate=learning_rate,momentum=0.9)NAG
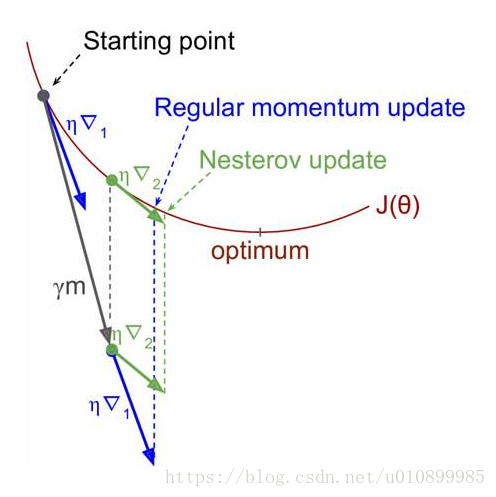
NAG(Nesterov Accelerated Gradient),,由Ilya Sutskever(2012 unpublished)在Nesterov工作的啟發下提出的。對動量梯度下降演算法的改進版本,其速度更快。其變化之處在於計算“超前梯度”更新動量項 γm,具體公式如下:
既然引數要沿著動量項 γm更新,不妨計算未來位置(θ -γm)的梯度,然後合併兩項作為最終的更新項,其具體效果如圖1所示,可以看到一定的加速效果。
momentum基礎上設定 use_nesterov=True
tf.train.MomentumOptimizer(learning_rate=learning_rate,momentum=0.9, use_nesterov=True)AdaGrad
AdaGrad是Duchi在2011年提出的一種學習速率自適應的梯度下降演算法。在訓練迭代過程,其學習速率是逐漸衰減的,經常更新的引數其學習速率衰減更快,這是一種自適應演算法。其更新過程如下:
每步迭代過程:
- 從訓練集中的隨機抽取一批容量為m的樣本{x1,…,xm},以及相關的輸出yi
- 計算梯度和誤差,更新r,再根據r和梯度計算引數更新量:
其中,全域性學習速率 ϵ, 初始引數 θ,梯度平方的累計量r初始化為0), δ(通常為10^−7)是為了防止分母的為 0。
由於梯度平方的累計量r逐漸增加的,那麼學習速率是衰減的。考慮下圖所示的情況,目標函式在兩個方向的坡度不一樣,如果是原始的梯度下降演算法,在接近坡底時收斂速度比較慢。而當採用AdaGrad,這種情況可以被改善。由於比較陡的方向梯度比較大,其學習速率將衰減得更快,這有利於引數沿著更接近坡底的方向移動,從而加速收斂。對於每個引數,隨著其更新的總距離增多,其學習速率也隨之變慢。
缺點: 任然要設定一個變數ϵ ,經驗表明,在普通演算法中也許效果不錯,但在深度學習中,深度過深時會造成訓練提前結束。
tf.train.AdagradOptimizer(learning_rate=0.001).minimize(loss)Adadelta
Adadelta是對Adagrad的擴充套件,最初方案依然是對學習率進行自適應約束,但是進行了計算上的簡化。
Adagrad會累加之前所有的梯度平方,而Adadelta只累加固定大小的項,並且也不直接儲存這些項,僅僅是近似計算對應的平均值。即:
其中,η是學習率,gt 是梯度
在此處Adadelta其實還是依賴於全域性學習率的,但是作者做了一定處理,經過近似牛頓迭代法之後:
其中,E代表求期望。此時,可以看出Adadelta已經不用依賴於全域性學習率了。
tf.train.AdadeltaOptimizer(learning_rate=0.001).minimize(loss)RMSProp
RMSprop是對Adagrad演算法的改進,主要是解決。其實思路很簡單,類似Momentum思想,引入一個衰減係數,讓梯度平方的累計量r 每回合都衰減一定比例:
其中,衰減係數ρ
decay: 衰減率
epsilon: 設定較小的值,防止分母的為 0.
tf.train.RMSPropOptimizer(learning_rate=0.001,momentum=0.9, decay=0.9, epsilon=1e-10)優點:
- 相比於AdaGrad,這種方法有效減少了出現梯度爆炸情況,因此避免了學習速率過快衰減的問題。
- 適合處理非平穩目標,對於RNN效果很好
缺點:
- 又引入了新的超參—衰減係數ρ
- 依然依賴於全域性學習速率,
總結:RMSprop算是Adagrad的一種發展,和Adadelta的變體,效果趨於二者之間。
Adam
自適應矩估計(daptive moment estimation,Adam),是Kingma等在2015年提出的一種新的優化演算法,本質上是帶有動量項的RMSprop,其結合了Momentum和RMSprop演算法的思想。它利用梯度的一階矩估計 和 二階矩估計 動態調整每個引數的學習率。
具體實現每步迭代過程:
- 從訓練集中的隨機抽取一批容量為m的樣本{x1,…,xm},以及相關的輸出yi
- 計算梯度和誤差,更新r和s,再根據r和s以及梯度計算引數更新量 :
其中,一階動量s,二階動量r(初始化為0),一階動量衰減係數ρ1, 二階動量衰減係數ρ2
超引數的建議值是ρ1=0.9,ρ2 =0.999,epsilon: 設定較小的值,防止分母的為 0。
實踐
各種優化方法在CIFAR-10影象識別上比較:
- 自適應優化演算法在訓練前期階段在訓練集上收斂的更快,但是在測試集上反而並不理想。
- 用相同數量的超引數來調參,SGD和SGD +momentum 方法效能在測試集上的額誤差好於所有的自適應優化演算法,儘管有時自適應優化演算法在訓練集上的loss更小,但是他們在測試集上的loss卻依然比SGD方法高,
總結:
- 對於稀疏資料,優先選擇學習速率自適應的演算法如RMSprop和Adam演算法,而且最好採用預設值,大部分情況下其效果是較好的
- SGD通常訓練時間更長,容易陷入鞍點,但是在好的初始化和學習率排程方案的情況下,結果更可靠。
- 如果要求更快的收斂,並且較深較複雜的網路時,推薦使用學習率自適應的優化方法。例如對於RNN之類的網路結構,Adam速度快,效果好,而對於CNN之類的網路結構,SGD +momentum 的更新方法要更好(常見國際頂尖期刊常見優化方法).
- Adadelta,RMSprop,Adam是比較相近的演算法,在相似的情況下表現差不多。
- 在想使用帶動量的RMSprop,或者Adam的地方,大多可以使用Nadam取得更好的效果。
- 特別注意學習速率的問題。學習速率設定得非常大,那麼訓練可能不會收斂,就直接發散了;如果設定的比較小,雖然可以收斂,但是訓練時間可能無法接受。理想的學習速率是:剛開始設定較大,有很快的收斂速度,然後慢慢衰減,保證穩定到達最優
- 其實還有很多方面會影響梯度下降演算法,如梯度的消失與爆炸,梯度下降演算法目前無法保證全域性收斂還將是一個持續性的數學難題。
參考: