Given a string S, find the longest palindromic substring in S. You may assume that the maximum length of S is 1000, and there exists one unique longest palindromic substring.

解：樸素的想法是以i為中心，不斷向2邊尋找回文，用陣列P[i]記錄長度最長的值，由於“aa”這樣偶數個的迴文串沒有中心，我們先將原字串補齊成“￥#a#a#”，再來進行統計，這樣得到的P[i]有如下性質：

新串:　　　　# w # a # a # b # w # s # w # f # d #
輔助陣列P： 　　1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1

P[i]記錄的是以i為中心最長迴文串在新字串向右延伸的位數（包括它自己！！），可以看到P[i]-1正好是此最長迴文字串在原字串中的長度。
這樣的複雜度為O（n*n）。

Manacher方法O（n）：
在上面的基礎上利用到了迴文字串的性質，如下圖：

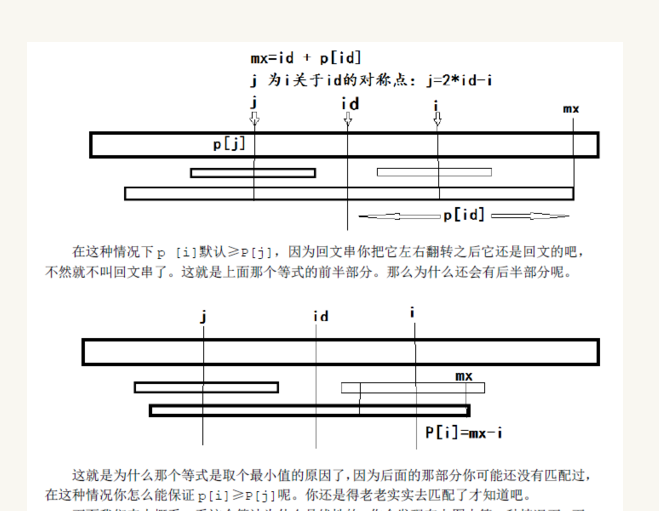
計算P[i]的時候我們利用前面的已找到的資訊，由於是迴文串，那麼前面的最長子串如果很長，假設是以id為中心，長度為P[id],那麼對於i，其關於id對稱點為j = 2 * id - i：

if id + P[id] > i:#如果當前中心在原來的子串範圍內
    P[id] = min(P[j],P[id] + id - i)#這裡就是上圖的2種情況
 

else:
    P[id] = 0
#下面接著一個個挨著比較和第一種方法一樣

這演算法是線性的原因是：我們可以看到僅當沒有比較過的迴文，我們才會繼續下去比較，不然就包含在圖中的情況中了，所以是線性的，僅比較未比較過的字元

class Solution(object):
    def longestPalindrome(self, s):
        """
        :type s: str
        :rtype: str
        """
        max = 0
        PLen = [0]*3000
        resCenter = 1
        if
 
 len(s) == 0 | len(s) == 1:
            return(s)
        NewS = "$#"
        for i in range(0,len(s)):
            NewS += s[i]
            NewS += '#'
        for i in range(1,len(NewS)):
            #j is the symmetry point of resCenter for i
            j = 2 * resCenter - i
            k = 0       
            #if max > i - resCenter:
            #   if max - i > p[j]:
            #       PLen[i] = PLen[j] 此時PLen[i]已經定型
            #   else:
            #       PLen[i] = max - i 此時PLen[i]還可以往後加

            if max + resCenter > i:
                PLen[i] = min(PLen[j],max + resCenter - i)
            else:
                PLen[i] = 0
            #接下來就直接從k開始比較
            k = PLen[i]
            while (i - k >= 0) & (i + k < len(NewS)):
                if NewS[i - k] == NewS[i + k]:
                    PLen[i] += 1
                    if max < PLen[i]:
                        max = PLen[i]
                        resCenter = i
                    k += 1
                else:
                    break
        max = int((max - 1)/2)
        if NewS[resCenter] == '#':
            resCenter = int(resCenter / 2 - 1)
            return (s[resCenter - max + 1:resCenter + max + 1])
        else:
            resCenter = int(resCenter / 2 - 1)
            return (s[resCenter - max:resCenter + max + 1])

python 的a[m:n]是取的m 到 n - 1!