根據二叉樹的前序和中序求後序
在面試的過程中,發現有幾家公司都喜歡考這樣的一道題,就是在一棵二叉樹中,已知這棵二叉樹的前序和中序遍歷結果,要求寫出後序遍歷結果。
例如:在一棵二叉樹總,前序遍歷結果為:ABDGCEFH,中序遍歷結果為:DGBAECHF,求後序遍歷結果。
我們知道:
前序遍歷方式為:根節點->左子樹->右子樹
中序遍歷方式為:左子樹->根節點->右子樹
後序遍歷方式為:左子樹->右子樹->根節點
從這裡可以看出,前序遍歷的第一個值就是根節點,然後再中序遍歷中找到這個值,那麼這個值的左邊部分即為當前二叉樹的左子樹部分前序遍歷結果,這個值的右邊部分即為當前二叉樹的右子樹部分前序遍歷結果。因此,通過這個分析,可以恢復這棵二叉樹,得到這樣的一段偽碼:
節點 getRoot(前序,中序)
c=前序第一個字元
pos=c在中序中的位置
len1=中序pos左半部分長度
len2=中序pos右半部分長度
新建節點r,令r的元素等於c
r的左兒子=getRoot(前序位置1開始的len1長度部分,中序pos位置的左半部分)
r的右兒子=getRoot(前序位置len1開始右半部分,中序pos位置的右半部分)
return r
如圖1示:
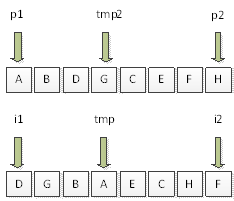
圖1
輸入前序ABDGCEFH,中序DGBAECHF,可以得出
A為該二叉樹的根節點
1: BDG為該二叉樹左子樹的前序
2: DGB為該二叉樹左子樹的中序
根據1和2可以構建一棵左子樹
3: CEFH為該二叉樹右子樹的前序
4: ECHF為該二叉樹右子樹的中序
根據3和4可以構建一個右子樹
執行至該步驟的時候就得到了該二叉樹的雲結構,如圖2所示,A為根節點,BDG在它的左子樹上,CEFG在它的右子樹上。
如此遞迴即可以構建一棵完整的二叉樹
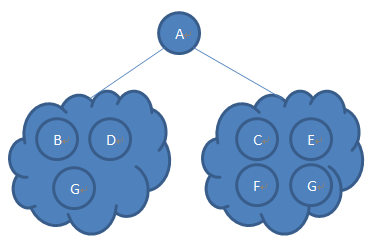
圖2
下面是c語言的實現方法(該程式碼的變數p1,p2,i1,i2,tmp請參考圖1):
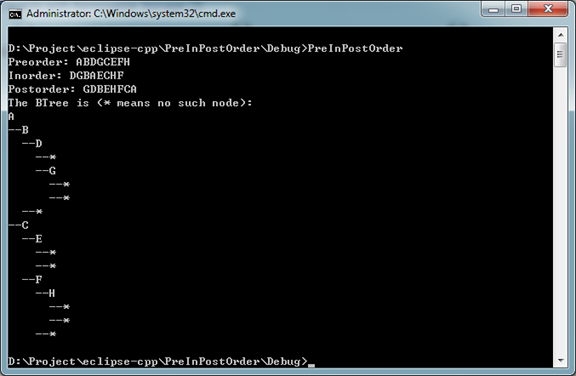
下面是輸出結果顯示: