一、背景

  蒙特卡羅模擬方法 (Monte Carlo simulation) 誕生於上個世紀40年代美國的”曼哈頓計劃”，名字來源於賭城蒙特卡羅。蒙特卡羅演算法從某種意義上而言，就是一種賭博演算法。
  它是一種基於隨機試驗和統計計算的數值方法，也稱計算機隨機模擬方法或統計模擬方法。蒙特卡羅方法的數學基礎是概率論中的大數定律和中心極限定理。

二、演算法引入

  最早接觸到這類演算法應該是在高中或者初中階段，而且是一道送分題。即在一個正方形中有一個內接圓。現在在這個正方形內拋灑豆子。已知正方形面積為S，落在正方形內的豆子總數為 M$M$，其中落在內接圓內的豆子總數為 N$N$。請估算內接圓的面積。

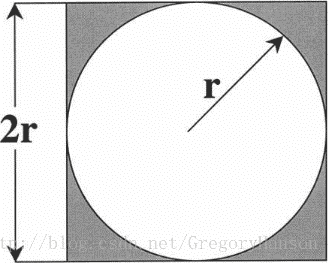
  根據概率論中的大數定律可知，當隨機事件發生的次數足夠多的時候（趨向於正無窮），其發生頻率就可作為此事件發生的概率。對於本題，當拋灑的豆子足夠多的時候，落在圓中的豆子比值即可視為圓與正方形面積的比值。那麼計算結果 S×N/M$S\times N/M$ 即為圓形面積。
  這種演算法需要承擔一定的風險，但是比起這種演算法帶給我們的收益，風險其實不足為懼，同時我們也可以運用合理恰當的方式來最小化這種風險。
  在建模和模擬中，應用蒙特卡羅方法主要有兩部分工作：用蒙特卡羅方法模擬某一過程時，產生所需要的各種概率分佈的隨機變數；用統計方法把模型的數字特徵估計出來，從而得到問題的數值解，即模擬結果。

解題步驟如下：
  1、根據提出的問題構造一個簡單、適用的概率模型或隨機模型，使問題的解對應於該模型中隨機變數的某些特徵（如概率、均值和方差等），所構造的模型在主要特徵參量方面要與實際問題或系統相一致。
  2、根據模型中各個隨機變數的分佈，在計算機上產生隨機數，實現一次模擬過程所需的足夠數量的隨機數。通常先產生均勻分佈的隨機數，然後生成服從某一分佈的隨機數，方可進行隨機模擬試驗。
  3、根據概率模型的特點和隨機變數的分佈特性，設計和選取合適的抽樣方法，並對每個隨機變數進行抽樣（包括直接抽樣、分層抽樣、相關抽樣、重要抽樣等）。
  4、按照所建立的模型進行模擬試驗、計算，求出問題的隨機解。
  5、統計分析模擬試驗結果，給出問題的概率解以及解的精度估計。

三、演算法應用

  蒙特卡羅演算法的應用領域很多，這個演算法在金融學、經濟學、工程學等領域得到了廣泛應用。適用於 Monte−Carlo$Monte-Carlo$ 演算法的問題，比較常見的有兩類。一類是問題的解等價於某事件的概率，如演算法引入中提到的求解圓的面積問題。另一類是判定問題，即判定某個命題是否為真，例如主元素存在性判定和素數的測試問題。
  對於第一類演算法所涉及到的問題，最多的就是定積分的求解。通常情況下我們有公式來求解各種圖形的面積，當然也可以求解定積分。但是當我們遇到不規則圖形以及極為複雜難以求解的定積分時，由於定積分的直觀意義就是函式曲線與 x$x$ 軸圍成的圖形中，y>

  對於蒙特卡羅演算法，其優缺點也是比較明顯的:
優點：
  1、能夠比較逼真的描述具有隨機性質的事物的特點及物理實驗過程
  2、受幾何條件限制小
  3、收斂速度與問題的維數無關
  4、誤差容易確定
  5、程式結構簡單，易於實現
缺點：
  1、收斂速度慢
  2、誤差具有概率性
  3、進行模擬的前提是各輸入變數是相互獨立的

四、演算法例項

例1:

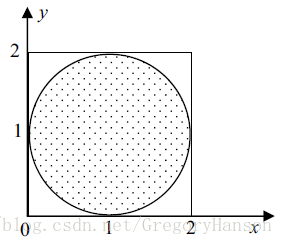
  在不知道求解圓面積的公式的情況下，試用蒙特卡羅法求出圓面積。

解答：
  由上文介紹可知，可在matlab中生成大量在 [0;2]$[0;2]$ 上服從均勻分佈的隨機數，從而模擬上文中的拋撒豆子。通過計算落在圓中的點與總點數，就可算出圓與正方形面積之比。

%Monte-Carlo
sita = 0:0.01:2*pi;
x = sin(sita);
y = cos(sita);%計算半徑為1的圓周上的點,以便做出觀察
m = 0;%計數器
x1 = 2*rand(1000,1) - 1;
y1 = 2*rand(1000,1) - 1;
N = 1000;%設定實驗次數
for n = 1:N
    p1 = x1(1:n);
    q1 = y1(1:n);
    if (x1(n) * x1(n) + y1(n) * y1(n)) < 1
        m = m + 1;
    end
    plot(p1,q1,'.',x,y,'-k',[-1 -1 1 1 -1],[-1 1 1 -1 -1],'-k');
    axis equal;
    axis([-2 2 -2 2]);
    text(-1,-1.2,['實驗總次數 n=',num2str(n)]); %顯示實驗結果
    text(-1,-1.4,['落入圓中數 m=',num2str(m)]);
    text(-1,-1.6,['近似圓面積 S_c=',num2str(m/n*4)]);
    set(gcf,'DoubleBuffer','on'); %雙緩衝避免作圖閃爍
    drawnow; %顯示結果
end

為了提升程式效率，可以取消模擬過程中間的視覺化顯示，並且利用 Matlab$Matlab$ 的矩陣運算來改造程式。
修改後程式碼如下：

ti                          % 計時器啟動
n=10000;                    % 每次隨機落點10000個
for k=1:1000                % 重複試驗1000次
    x1=2*rand(n,1)-1;
    y1=2*rand(n,1)-1;       % 隨機落點產生
    m(k)=sum((x1.*x1+y1.*y1)<1);% 求落入圓中的點數和
end
S_c=mean(m).*4./n           % 計算並顯示結果
time=toc                    % 顯示耗時

此例題方法可擴充套件到求解不規則圖形面積等問題上。求解所得結果會有很小的偏差，當生成的隨機點數足夠多時，此誤差可忽略不計。

例2:
  用蒙特卡洛法求解積分 ∫6013xdx${\int }_0^6\frac{1}{3}xdx$ 。

求解：

clear
clc
n=10000;
tol=[];
for i=1:10000
    x1=6*rand(n,1);
    y1=2*rand(n,1);
    tol(i)=sum(x1.*(1/3)>y1);
end
S=mean(tol).*12./n;

  口算該積分值可得答案為6。如果用蒙特卡羅演算法計算，撒10000個點可得到值為6.0007，誤差僅為0.0007，相對於6這個結果已經可以忽略不計。
  該程式碼中每次計算撒了10000個點。蒙特卡羅演算法得到的解的準確率會隨著撒點次數的增大而提升，這是蒙特卡羅演算法的優點同時也是它的弊端。當模擬情形過於複雜時，若要得到一個比較精確的結果，大量的模擬次數會使程式執行時間過長。所以何時使用蒙特卡羅演算法要從多方面考慮，蒙特卡羅演算法在硬體配置的約束下，並不是一種萬能解法。

  當然數學建模比賽中並不大可能直接要你求解某個不規則圖形的面積。很多的演算法理解起來或者運用起來並不難，多數難點在於，隊員能否發現某個問題與某種演算法是契合的。也就是能否讓人發出“我X，這個演算法還能這樣用啊！”的感嘆。蒙特卡羅演算法也是一樣。

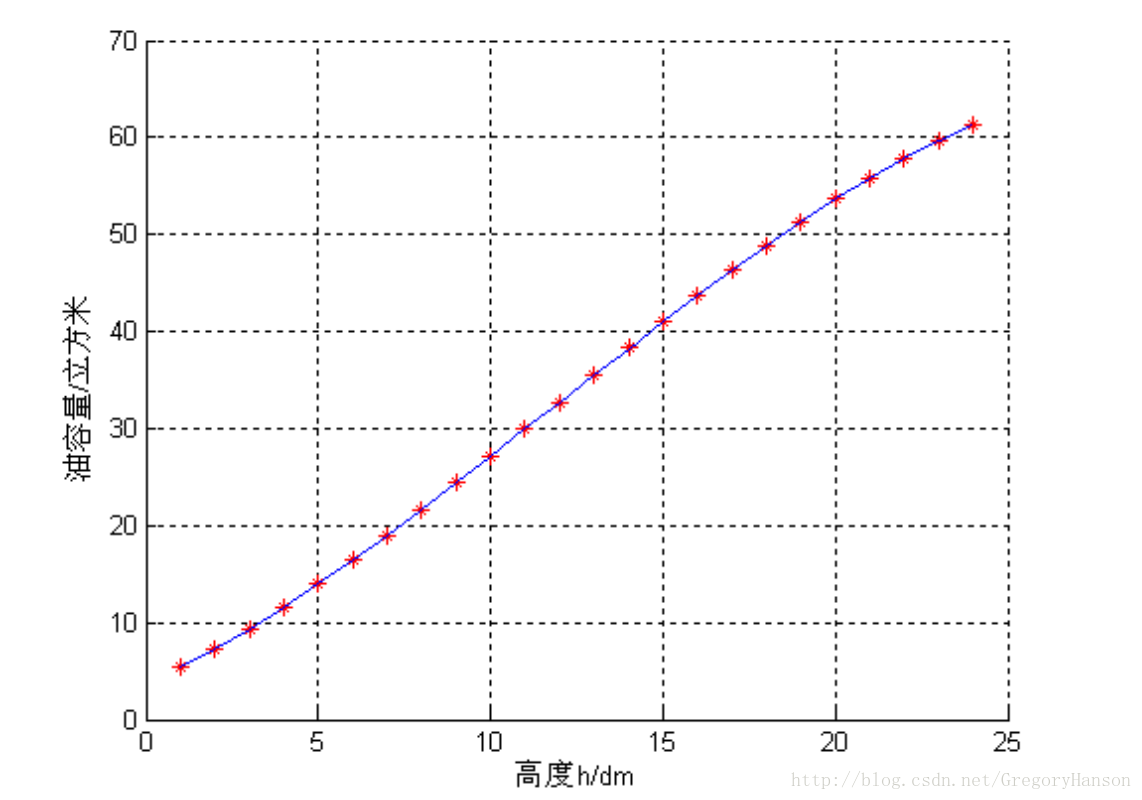
  靈活運用蒙特卡羅演算法的一個比較經典的例子就是2010年國賽A題的儲油罐問題了。有興趣的朋友可以自行查詢原題，這裡不對題目再做贅述。
  以下是網上一篇優秀論文在該題中利用蒙特卡羅法解題的方式。

六 模型的檢驗與評價
6.1 模型的檢驗（蒙特卡洛模擬方法）
  在實際儲油罐罐容表模型的建立和求解過程中，我們對球冠體內傾斜的部分燃油的體積進行了近似計算，忽略了一小部分球冠體體積。鑑於此，我們考慮通過用計算機模擬對該部分的體積進行模擬計算，觀察近似計算值與精確模擬數值的吻合情況，同時也對我們建立的模型進行驗證。
  模擬過程中的主要步驟：

Step1: 劃分空間，確定被忽略區域 Q$Q$ 的空間限制範圍，建立空間限制函式表示式。並尋求一包含該區域 Q$Q$ 的最小長方體。建立座標系，確定 Q$Q$ 所在的區域範圍；
Step2: 均勻做點，在長方體內分別從 x,y,z$x,y,z$ 三個座標軸依次等間距的產點 pi(xi,yi,zi)$p_i(x_i,y_i,z_i)$ ，記錄落入該區域的點以及生成的點的總數 M$M$ ，計算該長方體區域的總體積V$V$ ；
Step3: 統計落在該區域的點的個數，求該部分體積 VQ$V_Q$ ，計算公式為：

VQ=mM∗V$$V_Q=\frac{m}{M}\ast V$$

  在模擬中對不同區域分別進行求解所忽略部分的體積 VQ$V_Q$ ,再與所得到的理論值相加可得實際測量的精確值。根據蒙特卡洛模擬得到的被省略部分的體積，我們可以畫出實際體積和近似體積的差別圖。

  該論文非常巧妙的將蒙特卡羅演算法用於模型的檢驗而不是用於模型的求解，靈活的利用了蒙特卡羅演算法的特性，得到了較優的結果。

五、演算法擴充套件——拉斯維加斯演算法

  蒙特卡羅是一類隨機方法的統稱。這類方法的特點是，可以在隨機取樣上計算得到近似結果，隨著取樣的增多，得到的結果是正確結果的概率逐漸加大，但在（放棄隨機取樣，而採用類似全取樣這樣的確定性方法）獲得真正的結果之前，無法知道目前得到的結果是不是真正的結果。
  拉斯維加斯方法是另一類隨機方法的統稱。這類方法的特點是，隨著取樣次數的增多，得到的正確結果的概率逐漸加大，如果隨機取樣過程中已經找到了正確結果，該方法可以判別並報告，但在但在放棄隨機取樣，而採用類似全取樣這樣的確定性方法之前，不保證能找到任何結果（包括近似結果）。
  有興趣的同學可以查詢資料進行深入瞭解。