一）空間域濾波與頻率域濾波

 1）空間域濾波

      空間域濾波是指在影象空間中藉助模板對影象領域進行操作，處理影象每一個畫素值。主要分為線性濾波和非線性濾波兩類，根據功能可分為平滑濾波器和銳化濾波器。平滑可通過低通來實現，平滑的目的有兩類，一是模糊，目的是在提取較大的目標前去除太小的細節或將目標內的小尖端連線起來；二是去噪。銳化則可用高通濾波來實現，銳化的目的是為了增強被模糊的細節。

      在matlab中實現空間域濾波，有很多型別，如均值、中值、索貝爾、高斯、拉普拉斯、高斯-拉普拉斯等，但各有差異。下面是用matlab實現的程式碼：

%空間域濾波
clc;close all;
I=imread('1.tif');
w1=fspecial('average',[3 3]);
w2=fspecial('sobel');
w3=fspecial('gaussian',[3 3],0.5);
w4=fspecial('laplacian',0.2);
w5=fspecial('log',[5 5],0.5);
g1=imfilter(I,w1,'replicate');
g2=imfilter(I,w2,'replicate');
g3=imfilter(I,w3,'replicate');
g4=imfilter(I,w4,'replicate');
g5=imfilter(I,w5,'replicate');
g6=medfilt2(I);
subplot(3,3,1);imshow(I);title('原圖');
subplot(3,3,2);imshow(g1);title('均值濾波');
subplot(3,3,3);imshow(g2);title('索貝爾濾波');
subplot(3,3,4);imshow(g3);title('高斯濾波');
subplot(3,3,5);imshow(g4);title('拉普拉斯濾波');
subplot(3,3,6);imshow(g5);title('高斯-拉普拉斯濾波');
subplot(3,3,7);imshow(g6);title('中值濾波');
 

其執行結果如下：

    空間域濾波均採用matlab自帶的函式，引數也採用預設的值，可見中值濾波的效果最好。

    其中各濾波器的原理和優缺點如下：

   A)均值濾波：由fspecial函式生成的w1是一個大小為3*3的矩形平均濾波器，再用imfilter這個函式使這個掩模的中心逐個滑過影象的每個畫素，輸出為模板限定的相應領域畫素與濾波器係數乘積結果的累加和。由處理結果可見均值濾波器的效果使每個點的畫素都平均到它的領域去了，噪聲明顯減少了很多，效果較好。

   B)索貝爾濾波：w2是一個大小為3*3的sobel濾波器sv，用來近似計算垂直梯度，在影象的任何一點使用此運算元，將會產生對應的梯度向量或是其法向量。但是Sobel導數並不是真正的導數，這是因為Sobel運算元定義於一個離散空間之上，它真正表示的是多項式擬合，用較大的核的話會在更多畫素上進行擬合，會更加正確。而較小的核對噪聲會更加敏感，此時用sobel運算元近似計算導數的缺點精度比較低，這種不精確性在試圖估計影象的方向導數 (使用y/x濾波器響應的反正切得到的影象梯度的方向)。比如對於3*3的Sobel濾波器，梯度角度接近水平或者垂直方向的時候， 這樣的不準確性會比較明顯。由濾波效果可見到影象的邊緣凸顯了出來，sobel運算元主要用於邊緣檢測。

   C）高斯濾波：高斯濾波器是平滑線性濾波器的一種，線性濾波器很適合於去除高斯噪聲。而非線性濾波則很適合用於去除脈衝噪聲，中值濾波就是非線性濾波的一種。高斯濾波就是對整幅影象進行加權平均的過程，每一個畫素點的值，都由其本身和鄰域內的其他畫素值經過加權平均後得到。高斯濾波器是帶有權重的平均值，即加權平均，中心的權重比鄰近畫素的權重更大，這樣就可以克服邊界效應。高斯濾波如果採用3×3掩模的具體公式如下:

g(x,y)={f(x-1,y-1)+f(x-1,y+1)+f(x+1,y-1)+f(x+1,y+1)+[f(x-1,y)+f(x,y-1)+f(x+1,y)+f(x,y+1)]*2+f(x,y)*4}/16

其中，f(x,y)為原影象中（x,y)畫素點的灰度值，g(x,y)為經過高斯濾波和的值。由處理效果可看出高斯濾波的減噪能力較好。

   D）拉普拉斯濾波：拉普拉斯運算元是n維歐式空間的一個二階微分運算元。拉普拉斯運算元會突出畫素值快速變化的區域，因此常用於邊緣檢測。由效果可見影象的邊界得到了增強。

   E）中值濾波：中值濾波法是一種非線性平滑技術，它將每一畫素點的灰度值設定為該點某鄰域視窗內的所有畫素點灰度值的中值。中值濾波是基於排序統計理論的一種能有效抑制噪聲的非線性訊號處理技術，中值濾波的基本原理是把數字影象或數字序列中一點的值用該點的一個鄰域中各點值的中值代替，讓周圍的畫素值接近的真實值，從而消除孤立的噪聲點。方法是用某種結構的二維滑動模板，將板內畫素按照畫素值的大小進行排序，生成單調上升（或下降）的為二維資料序列。二維中值濾波輸出為g（x,y）=med{f(x-k,y-l),(k,l∈W)} ，其中，f(x,y)，g(x,y)分別為原始影象和處理後圖像。W為二維模板，通常為3*3，5*5區域，也可以是不同的的形狀，如線狀，圓形，十字形，圓環形等。中值濾波對於斑點噪聲和椒鹽噪聲來說尤其有用。儲存邊緣的特性使它在不希望出現邊緣模糊的場合也很有用。由上圖效果可見中值濾波的效果最好。

     由以上分析可知，各種濾波器各有優劣，適用情況也不盡相同，線性濾波器很適合於去除高斯噪聲，而非線性濾波則很適合用於去除脈衝噪聲，如中值濾波很適合去除椒鹽噪聲。使用起來要視具體實際情況而定。

2）頻率域濾波

  

     開始時看書看了些原理想自己用演算法實現發現有困難，就去百度了一下，寫了下面的一些程式碼：

%頻率域濾波
clc;close all;
f=imread('1.tif');
f=im2double(f);

F=fft2(double(f));%傅立葉變換

F=fftshift(F);%將變換的原點移到頻率矩形的中心
[M,N]=size(f);

%理想低通濾波

D0=input('輸入截止頻率');
h1=zeros(M,N);
for i=1:M
    for j=i:N
        if(sqrt(((i-M/2)^2+(j-N/2)^2))<D0)
            h1(i,j)=1;
        
        end
    end
end
G1=F.*h1;
G1=ifftshift(G1);
g1=real(ifft2(G1));

%巴特沃斯低通濾波
n=input('巴特沃斯濾波器的階數 n=');  
n1=fix(M/2);
n2=fix(N/2);
h2=zeros(M,N);
for i=1:M
    for j=1:N
        d=sqrt((i-n1)^2+(j-n2)^2);
        h2=1./(1+(d./D0).^(2*n));
       
    end
end
G2=F.*h2;
G2=ifftshift(G2);
g2=real(ifft(G2));

%高斯低通濾波
h3=zeros(M,N);
for i=1:M
    for j=1:N
        h3=exp(-(d.^2)./(2*(D0^2)));
    end
end
G3=F.*h3;
G3=ifftshift(G3);
g3=real(ifft(G3));

subplot(2,3,1);imshow(f);title('原圖');
subplot(2,3,2);imshow(g1);title('理想低通濾波');
subplot(2,3,3);imshow(g2);title('巴特沃斯低通濾波');
subplot(2,3,4);imshow(g3);title('高斯低通濾波');

其執行效果如下：

   可見出現了問題，理想低通濾波的效果並不好，巴特沃斯和高斯濾波器的輸出影象成了黑色，後經反覆檢查，除錯，並沒找出問題所在，於是打算嘗試另一種方法。程式碼和結果如下：

%巴特沃斯低通濾波
clc;close all;
f=imread('1.tif');
f=im2double(f);
M=2*size(I,1);
N=2*size(I,2);                        %濾波器的行列數  
u=-M/2:(M/2-1);
v=-N/2:(N/2-1);
[U,V]=meshgrid(u,v);
D=sqrt(U.^2+V.^2);
D0=50;                                %截止頻率
n=6;
H=1./(1+(D./D0).^(2*n));              %設計巴特沃斯濾波器
F=fftshift(fft2(I,size(H,1),size(H,2)));%傅立葉變換
G=F.*H;
L=ifft2(fftshift(G));                   %傅立葉反變換
L=L(1:size(I,1),1:size(I,2));
subplot(121);imshow(f);
subplot(122);imshow(L);

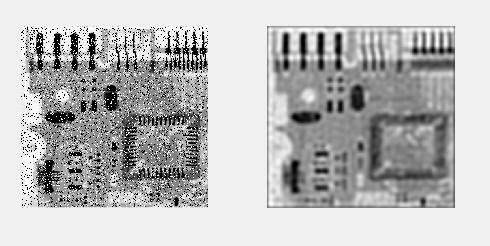
%高斯低通濾波
clc;close all;
I=imread('1.tif');  
I=im2double(I);  
M=2*size(I,1);
N=2*size(I,2);                        %濾波器的行列數  
u=-M/2:(M/2-1);
v=-N/2:(N/2-1);
[U,V]=meshgrid(u,v);
D=sqrt(U.^2+V.^2);
D0=20;
H=exp(-(D.^2)./(2*(D0^2)));          %設計高斯濾波器
J=fftshift(fft2(I,size(H,1),size(H,2)));
G=J.*H;
L=ifft2(fftshift(G));
L=L(1:size(I,1),1:size(I,2));
figure;
subplot(121);imshow(I);
subplot(122);imshow(L);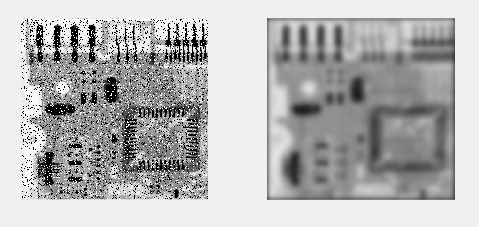 

    通過這種方法執行出的結果是正常的。低通濾波濾掉了影象頻譜中的高頻成分，僅讓低頻部分通過，即變化劇烈的成分減少了，結果是使影象便模糊。比較可見高斯濾波的效果最好。

   頻率域高通濾波和低通濾波實現的原理差不多，只是在設計濾波器時的公式有些差異，我就沒有再重複實現了。