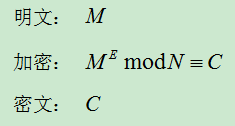前言：

• RSA公鑰加密演算法是第一個既能用於資料加密也能用於數字簽名的演算法。
• 易於理解和操作，所以十分流行。
• RSA演算法就是素數的一個典型的應用。

什麼是RSA:

• 在計算機中常用的加密解密技術分為兩類，即對稱加密和非對稱加密。對稱加密，非對稱加密上上一篇博文裡進行了淺析，有興趣可以查閱：安全加密
  
  
• 在對稱加密技術中，對資訊的加密和解密都使用相同的祕鑰key,也就是說使用同一個祕鑰key對資料進行加密和解密。這種加密方法可簡化加密解密的處理過程，資訊交換雙方不必彼此研究和交換專用的加密解密演算法。如果在交換階段，祕鑰key沒有洩露，那麼加密資料的機密性和報文的完整性就可以得到保證。
• 對稱加密技術雖然簡單，但是存在一些不足，由於加密、解密都需要使用同一個key,這樣，資訊傳送雙方都需要接觸這個key,祕鑰key更容易洩露。
  
  
  
• 而非對稱加密（又稱為公開祕鑰加密）中，不再只有一個祕鑰key了。在非對稱加密演算法中，祕鑰被分解為一對，一個成為公開祕鑰（簡稱公鑰PK）,另一個成為私有祕鑰（簡稱私鑰）。對應公鑰，可以通過非保密方式向他人公開，而私鑰則由解密方儲存，不用對別人公開。
• 傳送訊息的一方通過公鑰對資料進行加密，然後發給接收方。接收方通過私鑰對密文進行解密。
• 由於非對稱加密方式可以使通訊雙方無需事先交換祕鑰就可以建立安全通訊，因此被廣泛用於身份認證、數字簽名等資訊交換領域。
• 非對稱加密體系一般是建立在某些已知的數學難題上，是計算機複雜性理論發展的必然結果。最具有代表性的非對稱加密方式就是RSA公鑰密碼體制。

RSA演算法基礎

1.生成公鑰和私鑰：

（1）隨意選擇兩個大的素數P 和 Q，P不等於 Q
（2）將P、Q 兩個素數相乘得到一個數N,即N=PQ
（2）將P、Q 分別減一，再相乘，得到一個數 T，即T=(P-1)(Q-1)
（3）選擇一個整數E，作為一個祕鑰，使得E 與T 互質（即ET的最大公約數為 1），且E 必須小於T
（4）根據公式DE mod T ≡ 1,計算出D 的值，作為另一個祕鑰
（5）通過以上步驟計算得出N、E、D

這三個資料，其中（N、E）作為公鑰，（N、D）作為私鑰 （公私鑰交換也是ok的）.
（6）0生成公鑰私鑰後，就可以將公鑰對外公佈了
步驟圖示：

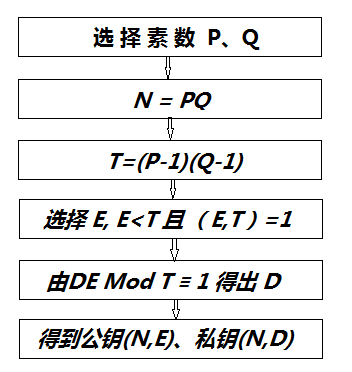
2.用公鑰加密資訊：

傳送資訊的一方收到公鑰PK 後，就可以通過公鑰PK 對資料進行加密。加密的操作步驟如下，其中明文為M, 加密後得到的密文為C，公鑰為（N，E）

3.用私鑰解密資訊：

接收方持有私鑰（N,D）,在接收到密文C 後，即可通過私鑰進行解密，得到明文M

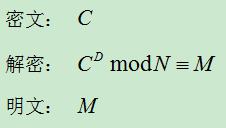
RSA演算法實踐

瞭解RSA的演算法生成祕鑰、加密、解密的過程後，現在進一步瞭解RSA的演算法使用過程吧。

1.生成公鑰PK和私鑰SK:

2.用公鑰加密：

為方便計算，取上面的（143,103）為公鑰，（143,7）為私鑰。
並假定明文為2，加密過程如下：

3.用私密解密

收到密文C（即63）後，則根據私鑰（143,7）進行解密，解密過程如下：

小結：

從上面生成的密文、加密、解密的過程可以看出，雖然我們只是使用了兩個小的素數11,13，但是計算量非常大，特別是加密和解密過程中，需要進行冪運算，得到的結果將是一個非常大的整數。在實際應用中，如果P、Q取很大值得素數，則得到的N、D、E 值也將會很大，所以在加密、解密過程的冪運算結果將會更加大。通過C語言提供的基本資料型別已經沒有辦法儲存這麼大的數了。