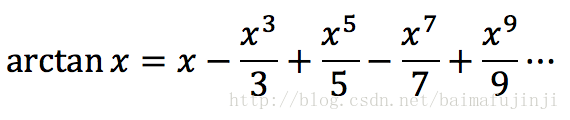各種求圓周率π的演算法(蒙特卡洛法的Java實現)
阿新 • • 發佈:2019-02-04
什麼是演算法?簡單地說,演算法就是有窮規則構成的用於解決某一類問題的運算序列或執行步驟。在《演算法之美:隱匿在資料結構背後的原理》第1章中我們講到要解決一個問題可能會有不同的方法,當時所舉的例子就是求圓周率π的近似值。對於這個問題你能想到多少種演算法呢?
彙集經典問題,暢享程式設計技法之趣;
點撥求職熱點,敲開業界名企之門。
方法(1):首先根據微積分中的泰勒公式,可以使用下面這個公式來求π的近似值
方法(2):其次可以還可以利用下面這個馬青公式來求解π的近似值:
馬青公式由英國天文學家約翰·馬青(John Machin,1686 –1751)於1706年發現,他利用這個公式計算到了100位的圓周率。此外,上式中的反三角函式可以領用下面這個泰來展開式進行計算:
方法(3):最後,也是我們準備來動手實踐一下的就是利用蒙特卡洛法。這個方法背後的理論基礎是概率論中的伯努利大數定律。眾所周知,圓的面積公式為 S = πr2,當 r =
1 時,S = π。如果在一個邊長為1的正方形中有一個內切圓,那麼該圓的面積就是π/4。利用這一原理,可以假設有大量的隨機點等概率均勻地落入此正方形中。若正方形的面積為S',內切圓的面積為S,如果落入正方形中的點數為 N',落入內切圓的面積為N,這時便有 S'/S = N'/N,所以可據此求得π = 4×N/N'。
下面就編寫一個Java程式來實現蒙特卡洛法求π的近似值:
-
import java.io.BufferedReader;
- import java.io.InputStreamReader;
- publicclass MonteCarloPi {
- publicstaticvoid main(String[] args) throws Exception{
- BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
- System.out.print("How many darts shoud I toss at the board?\n");
-
String s = br.readLine();
- int numberOfDarts = Integer.parseInt(s.trim());
- double radius = 1.0;
- Dartboard d = new Dartboard(radius);
- for(int i=1; i<=numberOfDarts; i++){
- Toss t = Toss.getRandom(radius);
- d.strike(t);
- }
- double fractionIn = d.getFractionIn();
- double pi = 4.0 * fractionIn;
- System.out.println("Pi is approximately "+pi);
- }
- }
- class Dartboard{
- privatedouble radius;
- privateint insideCircle, outsideCircle;
- public Dartboard(double radius){
- this.radius = radius;
- insideCircle = 0;
- outsideCircle = 0;
- }
- publicvoid strike(Toss toss){
- double x = toss.getX();
- double y = toss.getY();
- if(Math.sqrt(x*x + y*y) < radius)
- insideCircle++;
- else
- outsideCircle++;
- }
- publicdouble getFractionIn() {
- double total = (double) (insideCircle + outsideCircle);
- return (double) insideCircle/total;
- }
- }
- class Toss{
- privatedouble x,y;
- public Toss(double x, double y){
- this.x = x;
- this.y = y;
- }
- publicdouble getX(){return x;}
- publicdouble getY(){return y;}
- publicstatic Toss getRandom(double radius){
- double x,y;
- double size = Math.random();
- double sign = Math.random();
- size = size * radius;
- if(sign > 0.5)
- x = size;
- else
- x = -size;
- size = Math.random();
- sign = Math.random();
- size = size * radius;
- if(sign > 0.5)
- y = size;
- else
- y = -size;
- returnnew Toss(x,y);
- }
- }
執行一下上述程式碼,然後我們來驗證一下其效果如何...
- How many darts shoud I toss at the board?
- 1000000
- Pi is approximately 3.142028
可見所得到的結果較好地近似於圓周率 π 。
(本文完)