二分法是求方程近似解的一種簡單直觀的方法，設函式f(x)在[a,b]上連續，且f(a)*f(b)<0,則表明f(x)在[a,b]上至少有一個零點，這是微積分中的介值定理(不得不吐槽一下大學微分方程老師講課跟個煞筆一樣，反正我是重來沒聽的）．然後通過二分割槽間，縮小區間範圍，當小到一定的精確度的時候，這個x就是我們所求的近似根了．
個人對演算法的分析：１首先輸入我們的函式f(x),這裡定義為一元三次方程;2,輸入求根區間[a,b]和誤差控制量eps(在C語言中1e-10代表1*10的負10次方）,用到了fabs()求絕對值的數學庫函式．輸入步驟完畢．３，判斷f(a)*f(b)<0是否為真．為真代表有零點，就可以用二分法不斷地縮小空間，得出近似解x了．沒有零點就尷尬了，二分法只能計算方程的實根，這裡也可以看出二分法的侷限性．
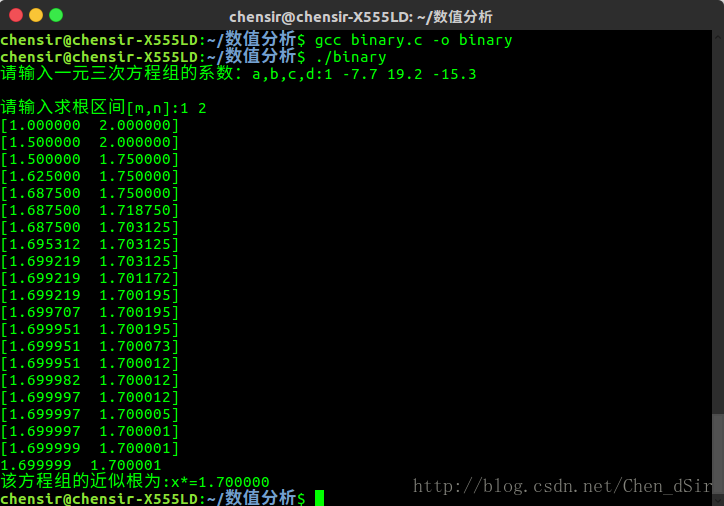
下面給出一個題目：用二分法求f(x)=x*x*x-7.7*x*x+19.2*x-15.3在區間[1,2]之間的根．
下面給出自己寫的程式碼，如下：

/********************************************
    > File Name: Binary.c
    > Author:chendiyang
    > School:WUST_CST_1501班
    > Myblog:www.chendsir.com
    > Mail:1441353519@qq.com 
    > Created Time: 2017年04月18日 星期二 23時55分13秒
 **************************************************/
#include <stdio.h>
 

#include <math.h>

const double eps = 1e-6; //定義我們計算的精度
double a,b,c,d;        //假定我們輸入的函式是一元三次方程組，a*x*x*x+b*x*x+c*x+d=0
double f(double x) //定義我們的函式
{
return a*x*x*x+b*x*x+c*x+d;
}

int main()
{
    double m,n;//求根區間[m,n]
    double i,j,sum;
    printf("請輸入一元三次方程組的係數：a,b,c,d:");
    scanf("%lf%lf%lf%lf
 
",&a,&b,&c,&d);
    printf("\n請輸入求根區間[m,n]:");
    scanf("%lf%lf",&m,&n);
    if(f(m)*f(n)<0)
    {
        while(fabs(m-n)>eps)
        {
          i=(m+n)/2.0;
          sum=f(i);
          printf("[%lf  %lf]\n",m,n);
          if(fabs(sum)<eps)
           {
               break;
            //printf("\n該方程組的近似根為:x2*=%lf\n",i);
            //return 1;
           }
          else if(f(i)*f(m)<0)
          {
              n=i; //修正區間，將[m,n]換成[m,i],這裡的i是中點
          }  
          else if(f(i)*f(n)<0)
          {
              m=i;//修正區間，將[m,n]換成[i,n],這裡的i是中點
          }
        }
    }
    else ; //如有其他求根方法，可以加上
    printf("%lf  %lf",m,n);
    j=(m+n)/2;
    printf("\n該方程組的近似根為:x*=%lf\n",j);
}

　　　這道題目就是不停的縮小區間，從而得出近似解，
　　　然而二分法最坑的地方不是它只能計算實根這個問題，最坑的是它當函式f(x)存在幾個零點實，它只能計算出一個零點！！這個針對有些演算法題目就不好辦了．牛頓迭代法和絃切法可以解決它的不足，當然也有它們的侷限，every coin has two sides,事物都有兩面性，演算法也不例外．．．