霍夫曼編碼(Huffman Coding)
霍夫曼編碼(Huffman Coding)是一種編碼方法,霍夫曼編碼是可變字長編碼(VLC)的一種。
霍夫曼編碼使用變長編碼表對源符號(如檔案中的一個字母)進行編碼,其中變長編碼表是通過一種評估來源符號出現機率的方法得到的,出現機率高的字母使用較短的編碼,反之出現機率低的則使用較長的編碼,這便使編碼之後的字串的平均長度、期望值降低,從而達到無失真壓縮資料的目的。
霍夫曼編碼的具體步驟如下:
1)將信源符號的概率按減小的順序排隊。
2)把兩個最小的概率相加,並繼續這一步驟,始終將較高的概率分支放在右邊,直到最後變成概率1。
3)畫出由概率1處到每個信源符號的路徑,順序記下沿路徑的0和1,所得就是該符號的霍夫曼碼字。
4)將每對組合的左邊一個指定為0,右邊一個指定為1(或相反)。
例:現有一個由5個不同符號組成的30個符號的字串:
BABACAC ADADABB CBABEBE DDABEEEBB
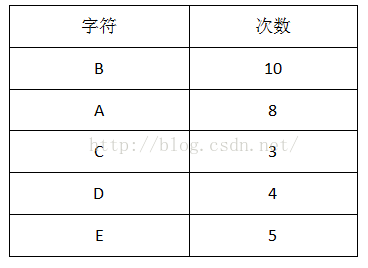
1首先計算出每個字元出現的次數(概率):
2把出現次數(概率)最小的兩個相加,並作為左右子樹,重複此過程,直到概率值為1

第一次:將概率最低值3和4相加,組合成7:
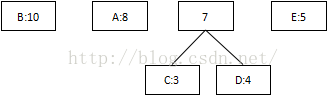
第二次:將最低值5和7相加,組合成12:

第三次:將8和10相加,組合成18:
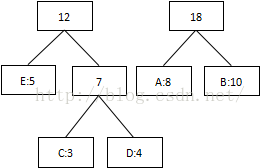
第四次:將最低值12和18相加,結束組合:
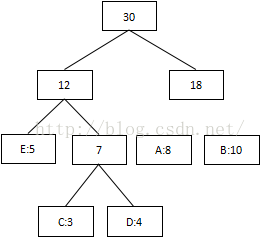
3 將每個二叉樹的左邊指定為0,右邊指定為1
 4 沿二叉樹頂部到每個字元路徑,獲得每個符號的編碼
4 沿二叉樹頂部到每個字元路徑,獲得每個符號的編碼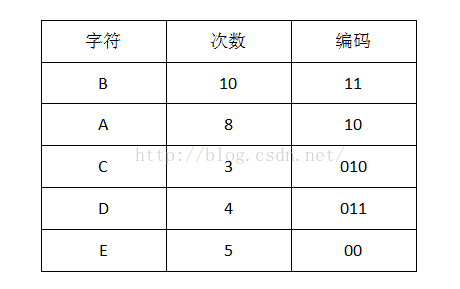
我們可以看到出現次數(概率)越多的會越在上層,編碼也越短,出現頻率越少的就越在下層,編碼也越長。
這裡需要注意的是,Huffman編碼使得每一個字元的編碼都與另一個字元編碼的前一部分不同,不會出現像’A’:00, ’B’:001,這樣的情況,解碼也不會出現衝突。
霍夫曼編碼的侷限性
利用霍夫曼編碼,每個符號的編碼長度只能為整數,所以如果源符號集的概率分佈不是2負n次方的形式,則無法達到熵極限;輸入符號數受限於可實現的碼錶尺寸;譯碼複雜;需要實現知道輸入符號集的概率分佈;
霍夫曼編碼實現 (C++實現):
int main()
{
int n, w;
char c;
string s;
cout << "input size of char : ";
cin >> n;
BinartNodes bn;
for(int i = 0; i != n; ++i)
{
cout << "input char and weight: ";
cin >> c >> w;
bn.add_Node((Node(c, w)));
cin.clear();
}
while(bn.size() != 1)
{
Node n1 = bn.pop(), //獲取前兩個權重最小的結點
n2 = bn.pop();
Node h(' ', n1.get_weight() + n2.get_weight()); //新建結點,權重為前兩個結點權重和
if( n1.get_weight() < n2.get_weight()) //權重較小的結點在新結點左邊
{
h.set(n1, n2); //設定新結點左右子結點
}
else
{
h.set(n2, n1);
}
bn.add_Node(h); //將新結點插入到multiset中
}
encodeing(bn.get_Node(), s); //編碼
cout << "input huffman code: ";
cin >> s;
cout << "decoded chars: ";
decoding(bn.get_Node(), s); //解碼
}Handle.h控制代碼類:
/*Handle.h*/
//控制代碼模型類
template <class Type> class Handle{
public:
Handle(Type *ptr = 0): pn(ptr), use(new size_t(1)) {}
Type& operator*(); //過載操作符*
Type* operator->(); //過載操作符->
const Type& operator*() const;
const Type* operator->() const;
Handle(const Handle &h): pn(h.pn), use(h.use) { ++*use; } //複製操作
Handle& operator=(const Handle &h); //過載操作符=,賦值操作
~Handle() {rem_ref(); } //解構函式
private:
Type *pn; //物件指標
size_t *use; //使用次數
void rem_ref()
{
if (--*use == 0)
{delete pn; delete use; }
}
};
template <class Type> inline Type& Handle<Type>::operator*()
{
if (pn) return *pn;
throw runtime_error("dereference of unbound Handle");
}
template <class Type> inline const Type& Handle<Type>::operator*() const
{
if (pn) return *pn;
throw runtime_error("dereference of unbound Handle");
}
template <class Type> inline Type* Handle<Type>::operator->()
{
if (pn) return pn;
throw runtime_error("access through unbound handle");
}
template <class Type> inline const Type* Handle<Type>::operator->() const
{
if (pn) return pn;
throw runtime_error("access through unbound handle");
}
template <class Type> inline Handle<Type>& Handle<Type>::operator=(const Handle &rhs)
{
++*rhs.use;
rem_ref();
pn = rhs.pn;
use = rhs.use;
return *this;
}/*Node.h*/
template <class T> class Handle;
class Node{
friend class Handle<Node>; //控制代碼模型類
public:
Node():ch(' '),wei(0), bits(), lc(), rc(){}
Node(const char c, const int w):
ch(c), wei(w), bits(), lc(), rc(){}
Node(const Node &n){ch = n.ch; wei = n.wei; bits = n.bits;
lc = n.lc; rc = n.rc; }
virtual Node* clone()const {return new Node( *this);}
int get_weight() const {return wei;} //獲取權重
char get_char() const {return ch; } //獲得字元
Node &get_lchild() {return *lc; } //獲得左結點
Node &get_rchild() {return *rc; } //獲得右結點
void set(const Node &l, const Node &r){ //設定左右結點
lc = Handle<Node>(new Node(l));
rc = Handle<Node>(new Node(r));}
void set_bits(const string &s){bits = s; } //設定編碼
private:
char ch; //字元
int wei; //權重
string bits; //編碼
Handle<Node> lc; //左結點控制代碼
Handle<Node> rc; //右結點控制代碼
};
inline bool compare(const Node &lhs, const Node &rhs); //multiset比較函式
inline bool compare(const Node &lhs, const Node &rhs)
{
return lhs.get_weight() < rhs.get_weight();
}
class BinartNodes{
typedef bool (*Comp)(const Node&, const Node&);
public:
BinartNodes():ms(compare) {} //初始化ms的比較函式
void add_Node(Node &n){ms.insert(n); } //增加Node結點
Node pop(); //出結點
size_t size(){return ms.size(); } //獲取multiset大小
Node get_Node() {return *ms.begin();} //獲取multiset第一個資料
private:
multiset<Node, Comp> ms;
};
/*Node.cpp*/
#include "Node.h"
Node BinartNodes::pop()
{
Node n = *ms.begin(); //獲取multiset第一個資料
ms.erase(ms.find(*ms.begin())); //從multiset中刪除該資料
return n;
}霍夫曼編碼實現 (C語言實現):
#include <stdio.h>
#include<stdlib.h>
#include<string>
#include <iostream>
#define MAXBIT 100
#define MAXVALUE 10000
#define MAXLEAF 30
#define MAXNODE MAXLEAF*2 -1
typedef struct
{
int bit[MAXBIT];
int start;
} HCodeType; /* 編碼結構體 */
typedef struct
{
int weight;
int parent;
int lchild;
int rchild;
char value;
} HNodeType; /* 結點結構體 */
/* 構造一顆哈夫曼樹 */
void HuffmanTree (HNodeType HuffNode[MAXNODE], int n)
{
/* i、j: 迴圈變數,m1、m2:構造哈夫曼樹不同過程中兩個最小權值結點的權值,
x1、x2:構造哈夫曼樹不同過程中兩個最小權值結點在陣列中的序號。*/
int i, j, m1, m2, x1, x2;
/* 初始化存放哈夫曼樹陣列 HuffNode[] 中的結點 */
for (i=0; i<2*n-1; i++)
{
HuffNode[i].weight = 0;//權值
HuffNode[i].parent =-1;
HuffNode[i].lchild =-1;
HuffNode[i].rchild =-1;
HuffNode[i].value=' '; //實際值,可根據情況替換為字母
} /* end for */
/* 輸入 n 個葉子結點的權值 */
for (i=0; i<n; i++)
{
printf ("Please input char of leaf node: ", i);
scanf ("%c",&HuffNode[i].value);
getchar();
} /* end for */
for (i=0; i<n; i++)
{
printf ("Please input weight of leaf node: ", i);
scanf ("%d",&HuffNode[i].weight);
getchar();
} /* end for */
/* 迴圈構造 Huffman 樹 */
for (i=0; i<n-1; i++)
{
m1=m2=MAXVALUE; /* m1、m2中存放兩個無父結點且結點權值最小的兩個結點 */
x1=x2=0;
/* 找出所有結點中權值最小、無父結點的兩個結點,併合並之為一顆二叉樹 */
for (j=0; j<n+i; j++)
{
if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)
{
m2=m1;
x2=x1;
m1=HuffNode[j].weight;
x1=j;
}
else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
{
m2=HuffNode[j].weight;
x2=j;
}
} /* end for */
/* 設定找到的兩個子結點 x1、x2 的父結點資訊 */
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight); /* 用於測試 */
printf ("\n");
} /* end for */
} /* end HuffmanTree */
//解碼
void decodeing(char string[],HNodeType Buf[],int Num)
{
int i,tmp=0,code[1024];
int m=2*Num-1;
char *nump;
char num[1024];
for(i=0;i<strlen(string);i++)
{
if(string[i]=='0')
num[i]=0;
else
num[i]=1;
}
i=0;
nump=&num[0];
while(nump<(&num[strlen(string)]))
{tmp=m-1;
while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1))
{
if(*nump==0)
{
tmp=Buf[tmp].lchild ;
}
else tmp=Buf[tmp].rchild;
nump++;
}
printf("%c",Buf[tmp].value);
}
}
int main(void)
{
HNodeType HuffNode[MAXNODE]; /* 定義一個結點結構體陣列 */
HCodeType HuffCode[MAXLEAF], cd; /* 定義一個編碼結構體陣列, 同時定義一個臨時變數來存放求解編碼時的資訊 */
int i, j, c, p, n;
char pp[100];
printf ("Please input n:\n");
scanf ("%d", &n);
HuffmanTree (HuffNode, n);
for (i=0; i < n; i++)
{
cd.start = n-1;
c = i;
p = HuffNode[c].parent;
while (p != -1) /* 父結點存在 */
{
if (HuffNode[p].lchild == c)
cd.bit[cd.start] = 0;
else
cd.bit[cd.start] = 1;
cd.start--; /* 求編碼的低一位 */
c=p;
p=HuffNode[c].parent; /* 設定下一迴圈條件 */
} /* end while */
/* 儲存求出的每個葉結點的哈夫曼編碼和編碼的起始位 */
for (j=cd.start+1; j<n; j++)
{ HuffCode[i].bit[j] = cd.bit[j];}
HuffCode[i].start = cd.start;
} /* end for */
/* 輸出已儲存好的所有存在編碼的哈夫曼編碼 */
for (i=0; i<n; i++)
{
printf ("%d 's Huffman code is: ", i);
for (j=HuffCode[i].start+1; j < n; j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf(" start:%d",HuffCode[i].start);
printf ("\n");
}
printf("Decoding?Please Enter code:\n");
scanf("%s",&pp);
decodeing(pp,HuffNode,n);
getchar();
return 0;
}