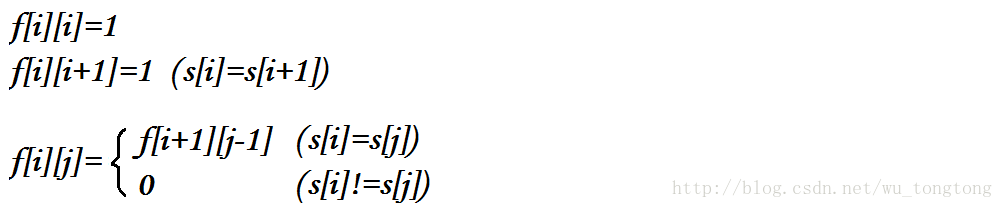Manacher演算法(最長迴文子串問題)
前言:
很久之前就聽到shallwe大爺提到過一種叫馬拉車的演算法。。。
問題描述
最長迴文子串問題:給定一個字串,求它的最長迴文子串長度
(注意,我們這裡說的子串一定是連續的,要與子序列區分開)
如果一個字串正著讀和反著讀是一樣的,那它就是迴文串。下面是一些迴文串的例項:
12321 a aba abba aaaa tattarrattat(牛津英語詞典中最長的迴文單詞)
暴力?
最簡單粗暴的方法:我們可以找到所有子串,暴力判斷是否迴文
因為每一個子串是由起點和終點確定的,所有一共有n^2個子串
複雜度O(n^3)
改進一下?
迴文,實際上就是中心對稱
因此我們可以列舉每一個位置,作為迴文子串的對稱軸,每次從中心像兩邊擴充套件
這裡要注意,迴文串要分成兩種情況:長度為奇數,長度為偶數
針對每一個位置,我們都要進行以上兩種嘗試
複雜度O(n^2)
好像還有n^2的方法
這麼經典的問題,當然可以用dp解決啦
設f[i][j]表示從i到j的字串是否是迴文串(bool型別的)
這樣我們就有轉移方程:
這裡就不得不提一句:
最長迴文子序列
經典解法就是dp,然而因為是子序列(不要求連續)
所以我們可以正反分別儲存原串,做兩個串的LCS即可
(LCS又可以視情況轉化成LIS完成,但這就是後話了)
Manacher 演算法
俗稱:馬拉車演算法
為眾位大神所青睞,是OI道路上的必備佳品
顯然,對於過長的字串,n^2的複雜度是無法承受的,所以我們需要一種更高效的演算法
首先我們先研究一下n^2演算法中我們都把時間浪費在了哪
- 由於迴文串長度的奇偶性造成了不同性質的對稱軸位置,要對兩種情況分別處理;
很多子串被重複多次訪問,造成較差的時間效率
簡單解釋一下缺陷二:char : a b a b a i : 0 1 2 3 4 //當i=1和i=2時,左邊的子串aba分別被遍歷了一次
如果我們能過通過某個擴充套件包修復這兩個bug的話,就可以大大的提高效率了
(1) 解決長度奇偶性帶來的對稱軸位置問題
馬拉車演算法首先對字串做一個預處理,
在每兩個字元之間(包括首尾)插入一個相同無效字元(在原串中沒有出現過),
這樣就會使所有的串都是奇數長度的
aba ---> #a#b#a#
abba ---> #a 這樣處理後,原串的迴文性質不受影響
原來是迴文的串仍是迴文串,原來不是迴文的串依然不是迴文
(2) 解決重複訪問的問題
我們把一個迴文串中最左或最右位置的字元與其對稱軸的距離稱為迴文半徑
Manacher定義了一個迴文半徑陣列RL
用RL[i]表示以第i個字元為對稱軸的迴文串的迴文半徑
我們一般對字串從左往右處理,因此這裡定義RL[i]為第i個字元為對稱軸的迴文串的最右一個字元與字元i的距離
char : # a # b # a #
RL : 1 2 1 4 1 2 1
RL-1 : 0 1 0 3 0 1 0
i : 0 1 2 3 4 5 6
char : # a # b # b # a #
RL : 1 2 1 2 5 2 1 2 1
RL-1 : 0 1 0 1 4 1 0 1 0
i : 0 1 2 3 4 5 6 7 8可以注意到,我們還寫出了RL-1的值
觀察一下可以發現,RL-1的值就是原串中以i為對稱軸的迴文串的長度
那麼如果我們得到了RL陣列,最長迴文子串就知道了
於是現在問題變成了:如何求解RL陣列(即以i為對稱軸的迴文串的最右端點)
原理:迴文串的對稱性
方法:分類討論+暴力擴充套件
之前我們已經說過:對字串一般從左往右處理
我們引入一個變數
同時記錄一下該回文串的對稱軸所在位置pos
因為我們是從左到右進行的
所以當前訪問位置一定在pos右邊
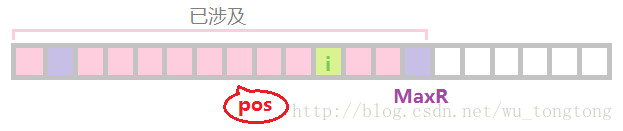
但我們更關注的是,i是在MaxRight的左邊還是右邊
我們分情況來討論
1)當i 在MaxR 左邊
兩個紫色格之內的字串是迴文的,
這種情況下,以
我們可以找到
這個
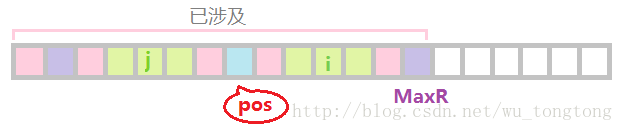
根據迴文的性質,以i為對稱軸的迴文串和以j為對稱軸的迴文串會有一部分相同
這裡我們又細分成兩種情況:
以
j 為對稱軸的迴文串比較短,兩端都沒有超過pos 代表的迴文串
我們可以肯定,RL[i]不會小於RL[j]
並且已經知道了部分的以i為中心的迴文串,於是可以令RL[i]=RL[j]
但是以i為對稱軸的迴文串可能實際上更長,因此我們試著以已經確定的區間為左右端點,繼續往左右兩邊擴充套件,直到左右兩邊字元不同,或者到達邊界以
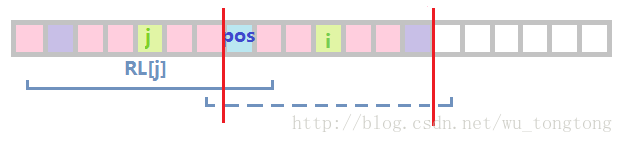
j 為對稱軸的迴文串很長
這時我們只能確定,兩條紅線之間的部分(即不超過MaxRight的部分)是迴文的,
於是從這個長度開始,嘗試向左右兩邊擴充套件,直到左右兩邊字元不同,或者到達邊界
不論以上哪種情況,之後都要嘗試更新MaxRight和pos,因為有可能得到更大的MaxRight。
1)當i 在MaxR 右邊(包括在MarR上)
遇到這種情況,說明以i為對稱軸的迴文串還沒有任何一個不煩被訪問過
這是我們只能從i開始向左右暴力擴充套件了
直到兩端的字元不同,或者到達字串邊界時停止
不要忘了更新
空間複雜度:插入分隔符形成新串,佔用了線性的空間大小;RL陣列也佔用線性大小的空間,因此空間複雜度是線性的
時間複雜度:對於每一個字元而言,操作只會進行一次,因此時間複雜度是O(n)
Code
雖然在分析的時候我們分成了好幾種情況
但是在程式碼中,我們可以把以上情況進行簡單的合併
注意,為了防止陣列越界,我們在最兩端增加一個互異特殊字元,所以演算法中字串是從1開始的
const int N=100010;
char ch[N]; //原字串
char s[N<<1]; //轉換後的字串
int RL[N<<1];
int init()
{
int len=strlen(ch);
s[0]='@'; //字串開頭增加一個特殊字元,防止越界
for (int i=1;i<=len*2;i+=2)
{
s[i]='#';
s[i+1]=ch[i/2];
}
s[2*len+1]='#';
s[2*len+2]='$';
return 2*len+1; //返回轉換字串的長度
}
int Manacher()
{
int len=init();
int MaxR=0,ans=0,pos=0;
for (int i=1;i<=len;i++)
{
int j=2*pos-i;
if (i<MaxR)
RL[i]=min(MaxR-i,RL[j]);
else RL[i]=1; //如果i>=MaxR,要從頭開始匹配
while (s[i-RL[i]]==s[i+RL[i]]) RL[i]++;
if (RL[i]+i>MaxR) { //更新pos和MaxR的值
MaxR=i+RL[i];
pos=i;
}
ans=max(ans,RL[i]);
}
return ans-1; //返回Len[i]中的最大值-1即為原串的最長迴文子串額長度
}