解釋

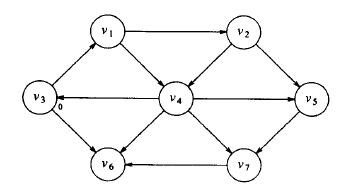
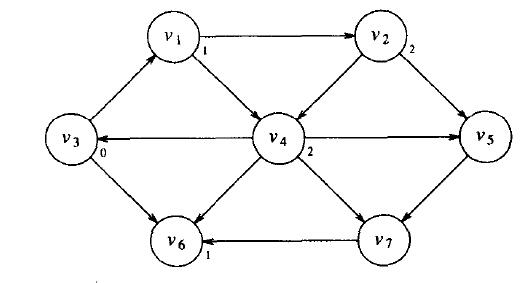
圖1

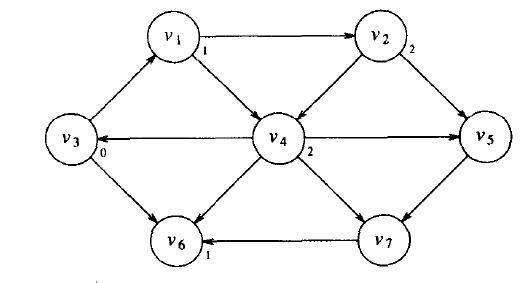
如圖1所示，這是一個有向無權圖，如果選中某個定點作為起始頂點s，我們要找出s到其他所有頂點的最短路徑問題。由於是無權的，所以我們只關心最短路徑所包含的邊數。這就是一個有向無權圖求最短路徑的問題，用到BFS演算法，廣義優先搜尋演算法。

流程解析

設s為選中的v3。

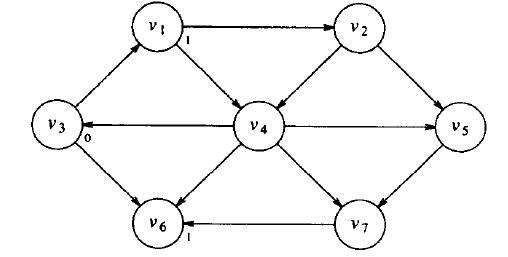
從s出發路徑長為1的頂點之後的圖

此時可以看到從s出發到v3的最短路徑長為0的路徑，只有v3自己。把這個標記下來。然後尋找所有從s出發路徑長為1的頂點，這些頂點可以通過考察s鄰接的頂點找到。

最後通過考察那些鄰接到剛被賦值的v2和v4的頂點可以發現，v5和v7各有一條三邊的最短路徑。現在所有頂點都已經計算。下圖顯示最終的演算法結果。

上述搜尋方法稱為廣度優先搜尋(breadth first search）。該方法是按層處理頂點：距開始點最近的那些頂點首先被求值，而最遠的那些頂點最後被求值。這很像對數的層序遍歷(level order traversal）。

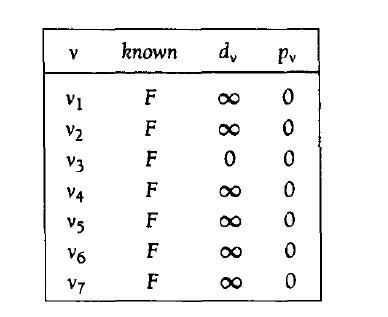
下圖是用於求無權最短路徑計算的表的初始配置

對於每個頂點，我們需要跟蹤三個資訊。known表示該頂點是否被處理，即求取到s的最短路徑；距離d為所求取的路徑長，開始被賦值無窮大，pv表示路徑，通過追溯pv可以顯示實際的路徑長。

演算法的虛擬碼如下

void Graph::unweighted(Vextex s)
{
    for each Vertex v
    {
        v.dist=INFINITY;
        v.known=false;
    }
    s.dist=0;
    for(int currDist=0;currDist<NUM_VERTICES;currDist++)
        for
 
 each Vertex v
            if(!v.known&&v.dist==currDist)
            {
                v.known=true;
                for each Vertex w adjacent to v
                    if(w.dist==INFINITY)
                    {
                        w.dist=currDist+1;
                        w.path=v;
                    }
            }
}

上述程式碼運算複雜度是O(V^2)

下面給出使用O(V+E）複雜度的演算法，類似於拓撲排序，使用連線表可以降低演算法的時間複雜度為O(V+E)。

void Graph::unweighted(Vertex s)
{
    Queue<Vertex> q;
    for each Vertex v
        v.dist=INFINITY'
    s.dist=0;
    q.enqueue(s);

    while(!q.isEmpty())
    {
        Vertex v=q.dequeue();
        for each Vertex w adjacent to v
            if(w.dist==INFINITY)
            {
                w.dist=v.dist+1;
                w.path=v;
                q.enqueue(w);
            }
    }

}

上述演算法的執行情況如下：

實際例子