求一個有向連通圖的割點，割點的定義是，如果除去此節點和與其相關的邊，有向圖不再連通，描述演算法。

-----------------------------------------

圖的割點問題，深度優先遍歷，如果某點的所有子孫節點與其祖先節點之間沒有相連的邊。

From : http://sokoban.ws/blog/?p=1000

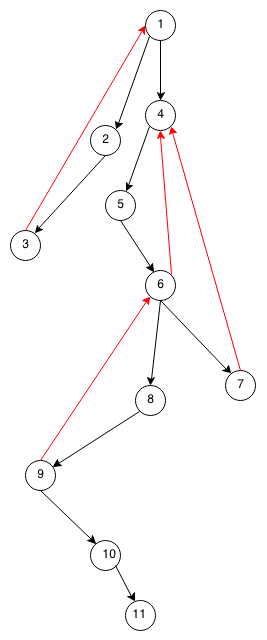
用DFS遍歷一個圖的所有頂點時，按訪問順序依次標號為1到n，稱之為DFS數。頂點v的DFS數記作D(v)。並得到一棵DFS樹（黑色邊），稱DFS樹的邊為樹邊（tree edge），其餘的邊（紅色邊）稱為回頭邊（back edge）。如下圖，圖的邊都按搜尋過程中向外的方向定向，得到一個有向圖。樹邊都是從DFS數小的頂點指向大的，回頭邊都是從DFS數大的頂點指向小的。

根據上面由深度優先搜尋得到的有向圖中，可定義每個頂點的低位數（lowpoint）：從該頂點出發，只用最多一條回頭邊，沿有向邊能走到的頂點中DFS數最小值。頂點v的低位數記為L(v)。

低位數取值有兩種情況：一是沒用上回頭邊，則能走到的DFS數最小的的頂點就是該點自身，對應的路是一個頂點構成的平凡的路。此時L(v)=D(v)。二是用了回頭邊，則一定是最後一條邊是回頭邊，走到一個DFS數更小的頂點。此時L(v)<=D(v)。

所以，一般地，總有L(v)<=D(v)。

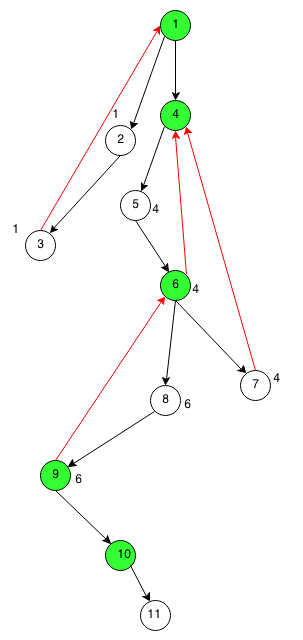
有了這兩個引數，就可以確定割點了：對根節點，即DFS數為1的頂點，其為割點當且僅當在DFS樹中有兩個或以上子節點

下圖標出的頂點的低位數（圈外數字，沒標圈外數字的頂點低位數和DFS數相等），綠色頂點為割點。

注：若用 DFS的深度（depth）來替代上面演算法中的DFS數，並用深度來計算低位數，則演算法一樣能有效地找出割點。

#include <iostream>
#include <math.h>
#define MAX_NUM 4
using namespace std;
/**
  * g is defined as : g[i][] is the out edges, g[i][0] is the edge count, g[i][1...g[i][0]] are the other end points.
*/
int cnt = 0;
int visit[MAX_NUM];
int lowest[MAX_NUM];
int cuts[MAX_NUM];
int dfs(int g[][MAX_NUM], int cuts[], int n, int s, int root) {
  int out = 0;
  int low = visit[s];
  for (int i = 1; i <= g[s][0]; ++i) {
    if (visit[g[s][i]] == 0) {
      ++out;
      visit[g[s][i]] = ++cnt;
      int clow = dfs(g, cuts, n, g[s][i], root);
      if (clow < low)
        low = clow;
    }
    else if (low > visit[g[s][i]])
      low = visit[g[s][i]];
  }
  lowest[s] = low;
  if (s == root && out > 1)
    cuts[s] = 1;
  return low;
}
void getCutPoints(int g[][MAX_NUM], int cuts[], int n) {
  memset(cuts, 0, sizeof(int) * n);
  memset(visit, 0, sizeof(int) * n);
  memset(lowest, 0, sizeof(int) * n);
  for (int i = 0; i < n; ++i) 
    if (visit[i] == 0) {
      visit[i] = ++cnt;
      dfs(g, cuts, n, i, i);
    }
}

int main() {
  int g[][MAX_NUM] = {{3,1,2,3}, {1,2,0,0}, {1,3,0,0}, {1,1,0,0}};
  getCutPoints(g, cuts, MAX_NUM);
  return 0;
}