以前一直沒有研究二進位制的移位運算的應用場景是什麼，怎麼運算？怎麼實現資料的四則運算的？ 直到最近，在看Think in
Java的書籍，才真正理解這個東西。下面記錄一下學習筆記。

1，二進位制

1.1 二進位制的表示

我們知道，計算機中所有資料都是以二進位制形式儲存。例如1（int）在二進位制中的表現形式就是
00000000 00000000 00000000 00000001。
而0的二進位制就是所有位上均為0。
具體的根據不同的程式語言，可能對於基礎資料型別有不一樣的位元組數的定義。
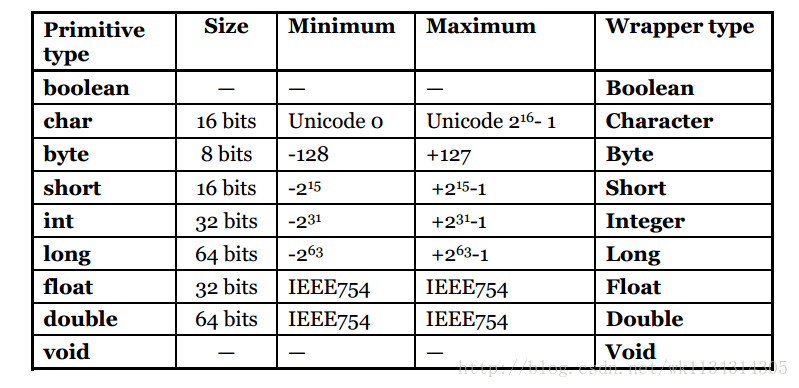
對於Java而言，Java的八大資料型別的位元組數定義如下：

byte:8bits
int:32bits
char:16bits
short
 
:16bits
long:64bits
boolean:-
float:32bits
double:64bits

以下是Think in Java中擷取的基礎資料型別的定義

1.2 二進位制資料與十進位制資料的關係

在二進位制中，5表示為101，也就是5=1*pow(2,2)+1*pow(2,0)

1.3 正負數

在二進位制中，需要有一個bit來表示是資料的正負，這bit就是資料的最高位。
1表示負數，0表示正數。

1.4 最大值和最小值

以int資料型別為例（下文中對於正數，如果位數沒有足夠的位數，筆者為了簡單，會忽略高位的0，而從第一個1開始）
例如，int型別的5在計算機中的表達就是101。既然資料型別有位元組數的限制，那麼必然就會有該資料型別能夠表達的範圍。int型別的資料有32bits，因此最多能夠表達的數字的個數就是2^32。

如果不考慮正負，那麼32bits的資料能夠表達的資料範圍就是
00000…….000000（32個0）~11111……..1111111（32個1），也就是0到2^32-1。
但是1.2節講到，資料有正負，因此在資料的表達範圍就發生了變化。其真正的表達範圍應該是
10000……000000（31個0）~011111……1111111（31個1）。也就是從 -2^31到2^31-1

看到這裡，讀者可能就有疑問了，為什麼不是從00000……000000到1111111……1111111呢？

1.2中已經說過，最高位的1代表負數，0代表正數。因為000000……000000000代表0，最高位的0已經被佔據了一位，那麼剩下的31個bit能夠表達的的數字也就是從0000……00000（31個0）到111111……11111（31個1），所以能夠表達的就是從0到2^31-1。同理，對於負數的範圍就是1000000……00000000到1111111……111111111，因此能夠表達的就是從 -2^31到-1。

那麼計算機中為什麼是10000……0000000代表最小的值呢？

這其實是二進位制的運算規則決定的。

例如，對於二進位制的-1，其二進位制的表達就是111111……111111，那麼加1，就應該等於0（也就是0000000……000000）

所以，上面的-1的表達就是1111111111……111111111，按照這樣的推算就可以知道最小數就是10000000……0000000000。
注：下面的部分會講解相反數的計算，以及二進位制資料的計算，這對於上面最大數最小數的表達的理解有幫助。

1.5 四則運算在二進位制中的表達

那麼，二進位制是怎麼進行計算的呢？

其實二進位制和十進位制的資料的計算規則也是一樣的。
在十進位制中，兩個數相加的規則就是“逢十進一”，對於二進位制同理，不過變成了“逢二進一”。相減就是如果被減數的位小於減數的位時，就向高位借1。

加法

規則：逢二進一
這裡上面的1.3的例子已經很好的講解了。那麼這裡還有一個問題，如果是按照逢二進一的規則，就會出現一種情況，就是最高位溢位的現象。也就是說最終計算出來的二進位制資料超出了位元組數的限制。那麼應該將最高位的那個bit應該捨棄。

上面的1.3的例子就是一個很好的例證。

減法

規則：如果被減數的對應位置的數小於減數的上的數，那麼就向其高位借2。簡稱”借一有二“

例如1-2=-1
即為:

    00000……00001
-   00000……00010
    ——————————————
    11111……11111

乘法

由於二進位制的乘法，每一位只有0和1，因此二進位制的乘法更簡單。

規則：
由低位到高位，用乘數的每一位去乘被乘數，若乘數的某一位為1，則該次部分積為被乘數；若乘數的某一位為0，則該次部分積為0。某次部分積的最低位必須和本位乘數對齊，所有部分積相加的結果則為相乘得到的乘積。

除法：
二進位制數除法與十進位制數除法很類似。

規則：先從被除數的最高位開始，將被除數（或中間餘數）與除數相比較，若被除數（或中間餘數）大於除數，則用被除數（或中間餘數）減去除數，商為1，並得相減之後的中間餘數，否則商為0。再將被除數的下一位移下補充到中間餘數的末位，重複以上過程，就可得到所要求的各位商數和最終的餘數。

1.6 相反數

二進位制中，對於相反數的計算，就是”取反加1“
例如-1的相反數就是1。
在二進位制中就是1111111……111111取反加1，得到00000……0000001。

2，位操作

二進位制的位操作主要有移位、位與、或、異或、非。
其中，對於char，byte，short都是以轉換為int進行移位操作的。而對於double和float都是沒有位操作的。

2.1移位

移位操作符有兩種，左移位<<和右移位>>，其中類似於+=這種操作符一樣，也有<<=和>>=。
左移：
例如，5<<2表示5向左移動兩位
5的二進位制表示就是101，那麼左移兩位之後，就是10100，也就是乘以4即等於20。
對於位數左移之後，低位的補0。
那麼比如10000……000000（即最小數），那麼它左移2位之後，它的二進位制表達就是00000000……000000（即為0）

public class BitCal {
    public static void main(String[] args) {
        int max_i=Integer.MIN_VALUE;
        System.out.println(Integer.toBinaryString(max_i));
        System.out.println(Integer.toBinaryString(max_i<<2));
    }
}

輸出的結果為：

10000000000000000000000000000000
0

右移：
和左移不一樣的地方就是：如果被位移的數是負數，那麼右移之後，高位全都補1；如果是正數，那麼右移之後，高位全都補0。也就是正數依然是正數，負數依然是負數。

無符號右移
這種移位操作與右移不同的地方就是：
無論是正數還是負數，在移位之後，高位都補0。即移位之後永遠都是正數。
注：

（1）無論是左移還是右移（包括無符號右移），都有一個共同的規則。 如果移動的位數超過規定的bit數，都會與最大移位數取模之後進行計算。

例如：
int型，32bits，如果是5<<33，其實就是5<<1；同理，右移和無符號右移也是一樣。
那麼對於long型資料，也是一樣。5<<65其實就是5<<1。

（2）對於byte和short進行移位運算的時候，他們會被轉換為int型。進行右移的時候，因為精度的原因（byte和short本身比int位元組少，因此轉成int計算完畢，再轉換回去的時候，可能會對高位截斷）
這個例子，可以參考《Think in Java》中的例子

如下：

package operators;

//: operators/URShift.java
// Test of unsigned right shift.
import static net.mindview.util.Print.print;

public class URShift {
  public static void main(String[] args) {
    int i = -1;
    print(Integer.toBinaryString(i));
    i >>>= 10;
    print(Integer.toBinaryString(i));
    long l = -1;
    print(Long.toBinaryString(l));
    l >>>= 10;
    print(Long.toBinaryString(l));
    short s = -1;
    print(Integer.toBinaryString(s));
    s >>>= 10;
    print(Integer.toBinaryString(s));
    byte b = -1;
    print(Integer.toBinaryString(b));
    b >>>= 10;
    print(Integer.toBinaryString(b));
    b = -1;
    print(Integer.toBinaryString(b));
    print(Integer.toBinaryString(b>>>10));
  }
} /* Output:
11111111111111111111111111111111
1111111111111111111111
1111111111111111111111111111111111111111111111111111111111111111
111111111111111111111111111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
11111111111111111111111111111111
1111111111111111111111
*///:~

筆者的疑惑
對於上面的第二條，《Think in Java》並沒有提到char，只是說byte和short位移的時候，可能出現這種意外。但是對於char型資料，
利用如下測試程式碼：

package baisc.bit;

public class BitCal {
    public static void main(String[] args) {
        char c1=(char)-1;
        System.out.println(Integer.toBinaryString(c1));
        c1>>=10;
        System.out.println(Integer.toBinaryString(c1));
        char c2=(char)-1;
        c2>>=17;
        System.out.println(Integer.toBinaryString(c2));
        char c3=(char)-1;
        c3>>=65;
        System.out.println(Integer.toBinaryString(c3));
        char u_c=(char)-1;
        u_c>>>=10;
        System.out.println(Integer.toBinaryString(u_c));
        short s=(short)-1;
        System.out.println(Integer.toBinaryString(s));
        s>>=33;
        System.out.println(Integer.toBinaryString(s));
    }
}

輸出結果如下：

1111111111111111
111111
0
111111111111111
111111
11111111111111111111111111111111
11111111111111111111111111111111

所以，問題來了

1）為什麼這裡的第一個輸出是16個1，而不是32個1，不是轉換成int計算的麼？
2）對於char型別的資料，右移和無符號右移都是高位補0麼？

如果有讀者瞭解這部分，希望能不吝賜教！

這裡可能需要了解一下Integer類的toBinaryString（）方法計算過程。

2.2 位與、或、異或、非

與：兩個bit都為1的時候，結果為，否則為0
或：兩個其中有一個為1即為1，否則為0
異或：相同為0，相異為1
非：0變1，1變0

3 &和&&、|和||的異同

對於boolean型別的資料，&和&&，|和||的計算結果相同。但是這裡有一處區別，按位與和按位或需要操作計算兩個二進位制的計算結果。但是如果是邏輯或，邏輯與，會有短路效應。可能只需要根據其中一個條件就可以判斷了，例如true||false只需要判斷前面一個就可以了，false&&false就只需要判斷前面一個就知道為false。