平衡查詢樹的目標是實現查詢、插入、刪除操作在最壞情況下的複雜度均為logN。

本節將介紹二三查詢樹。

二三樹中有兩種節點：

• 二節點對應一個鍵，有兩個子節點

• 三節點對應兩個鍵，有三個子節點

二三查詢樹非常平衡，每個空節點到根節點的距離都是一樣的 。

查詢操作

在二三樹中查詢一個鍵的時候有以下規則：

• 如果是二節點，二節點對應1個值，如果要查詢的值比該節點對應的值小，就往左側深入，反之亦成

• 如果是三節點，三節點對應2個值，如果比兩個值都小，就往左側深入，如果介於兩個值之間，就往中間深入，如果比兩個值都大，就往右側深入。

插入操作

根據查詢操作的規則，先定位到需要插入的節點。如果是二節點，那麼將二節點中增加一個鍵成為三節點。如果是三節點，在三節點中增加1個鍵成為四節點。由於四節點不允許在二三樹中出現，因此需要分解成兩個二節點，並且把中間的鍵提取到父節點中。下圖展示四節點分解的過程：

現在要在這棵樹中插入一個值7

首先根據查詢操作的規則定位到要插入的節點，定位之後是如圖所示的節點

由於該節點是三節點，因此插入一個鍵，使它成為四節點

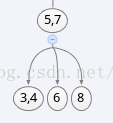
由於四節點不允許在2-3樹中存在，因此需要將其分解為兩個二節點，並把中間的鍵7提到父節點中

這樣插入操作就完成了

效能

2-3樹的高度介於lgN和log_3(N)之間，因此能夠保證所有的操作複雜度均在logN以下

實現

二三樹的實現非常複雜，因為要判斷每個節點的型別，插入節點的時候還需要判斷插入節點的位置，需要考慮的情況非常多。