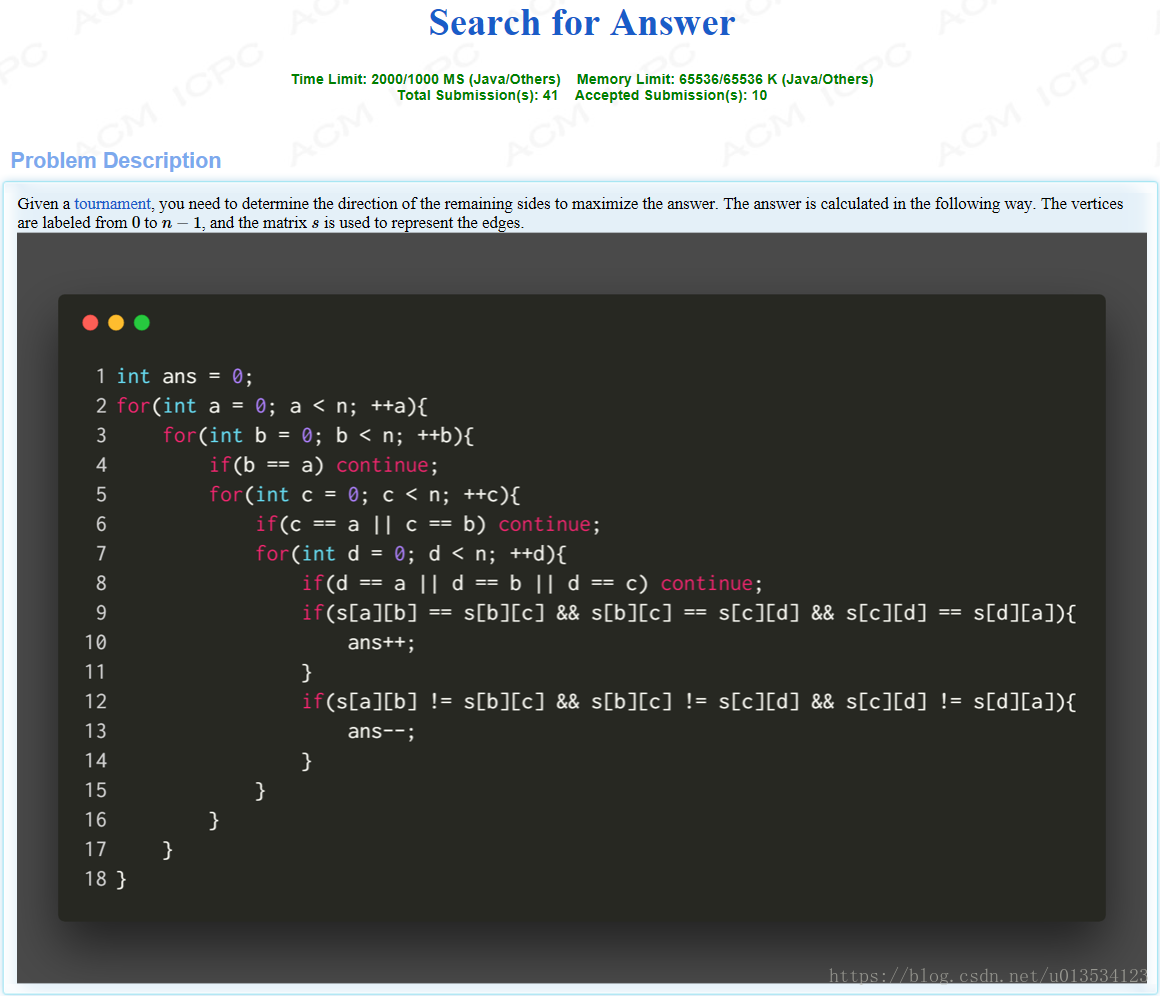
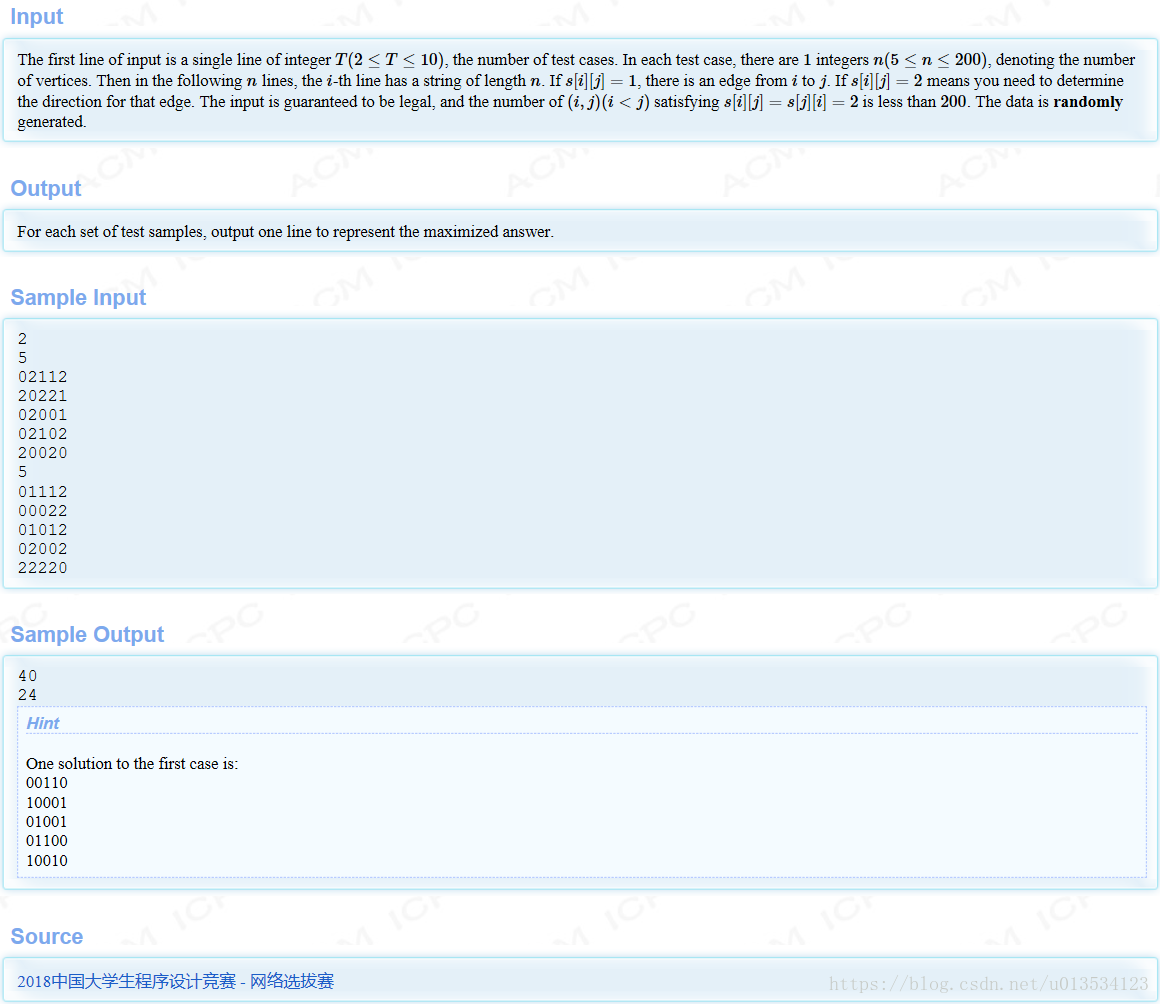
大致題意：給你一個競賽圖，告訴你一個記數方法，也即所有邊同向的四元組加一，所有相鄰兩邊方向相反的四元組減一。現在讓你最大化這個結果。

說實話，不看題解應該很難想到是一個費用流……題解給的也真是簡單，個人感覺還可能有錯？

我們可以這麼考慮，觀察它給的計數演算法，我們可以發現，他的總的迴圈次數是。於是我們不妨假設每一次迴圈都產生貢獻，然後減去那些實際上不產生貢獻和產生負貢獻的東西。考慮什麼樣的情況下不會產生貢獻，我們發現如果一個點，我選擇了任意兩條它的出邊以及對應的點，那麼不管第四個點是什麼，顯然構成的四元組一定不會有正的貢獻。而這樣的一個四元組在它的計數演算法中總共會被計算8次，正著迴圈4次，反著迴圈4次。如此一來，不會產生正的貢獻的方案數就是：

我們再來考慮重複的情況。根據我的演算法，會重複的沒有正貢獻的四元組，只有形如：a->b<-c->d<-a或a<-b->c<-d->a兩種形式。觀察這兩種形式發現，這兩種形式正好是會產生一個負貢獻的情況，而重複計算也正好知識重複計算了一次，也就是說這個重複正好幫我們處理的負貢獻的情況，可以不管這個重複。

如此，我們就有了大致的方法。對於已經確定的邊，我計算每個點的出度，然後帶入上式計算答案，不妨設為res。然後我們考慮那些不確定的邊。考慮構圖，把每一個不確定方向的邊(i,j)記錄一個編號x，連邊<i,x>和<j,x>，分別表示i->j和j->i，流量為1，費用為0。也即每條邊要麼正向，要麼反向。對於點i，如果新增加一條邊，那麼產生的貢獻就是deg[i]*(n-3)*8，即新產生的邊與之前每一條搭配一次，對應連邊<i',i>，流量為1，費用為deg[i]*(n-3)*8，同時更新度數。最後源點連線每一個i'，匯點連線每一個x。構圖完畢，跑一邊最小費用最大流即可。

關於證明的話，其實可以yy一下。一個點i'->i的次數越多，對應的費用就越高，我們要最大化ans，那麼就是要最小化費用，所以要在滿足每條邊都有確定方向的同時費用最小，對應就是最小費用流了。然後在實際操作中，*(n-3)*8是一個公因子，可以考慮最後再乘以它。設最小費用是cost，則最後的答案就是：

具體操作見程式碼：

#include<bits/stdc++.h>
#define LL long long
#define mod 998244353
#define pb push_back
#define lb lower_bound
#define ub upper_bound
#define INF 0x3f3f3f3f
#define sf(x) scanf("%d",&x)
#define sc(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define clr(x,n) memset(x,0,sizeof(x[0])*(n+5))
#define file(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout)

using namespace std;

const int N = 1e3 + 10;

struct Edge{int from,to,cap,flow,cost;};
int n,m,s,t,d[N];
int num[N][N],tot;

namespace MCMF
{
 	int n,m,s,t,d[N],p[N],a[N];
	vector<Edge>edges;
	vector<int>g[N];
	bool inq[N];

	void init(int a,int b,int c)
	{
		n=a; s=b; t=c;
		edges.clear();
		for(int i = 0;i<=n;i++)g[i].clear();
	}

	void AddEdge(int from,int to,int cap,int cost)
	{
		edges.push_back(Edge{from,to,cap,0,cost});
		edges.push_back(Edge{to,from,0,0,-cost});
		m=edges.size(); g[from].push_back(m-2); g[to].push_back(m-1);
	}

	bool BeintmanFord(int &flow,int &cost)
	{
		for(int i = 0;i<=t;i++)d[i]=INF;
		memset(inq,0,sizeof(inq));
		d[s]=0,a[s]=INF,inq[s]=1,p[s]=0;
		queue<int> q; q.push(s);
		while(!q.empty())
		{
            int u = q.front(); q.pop(); inq[u]=0;
			for(int i = 0;i<g[u].size();i++)
			{
				Edge &e = edges[g[u][i]];
				if(e.cap>e.flow&&d[e.to]>d[u]+e.cost)
				{
				 	d[e.to]=d[u]+e.cost; p[e.to]=g[u][i];
					a[e.to]=min(a[u],e.cap-e.flow);
					if(!inq[e.to]) {q.push(e.to); inq[e.to]=1;}
				}
			}
		}
		if(d[t]==INF)return false;
		flow+=a[t]; cost+=a[t]*d[t];
		int u = t;
		while(u!=s)
		{
           	edges[p[u]].flow+=a[t];
			edges[p[u]^1].flow-=a[t];
			u=edges[p[u]].from;
		}
		return true;
	}

    int Min_cost(int &flow,int &cost)
	{
	 	flow=0,cost=0;
		while(BeintmanFord(flow,cost));
		return cost;
	}
}

char ss[N][N];

int main()
{
    int T; sf(T);
    while(T--)
    {
        sf(n); tot=0;
        clr(d,n);
        for(int i=0;i<n;i++)
        {
            scanf("%s",ss[i]);
            for(int j=0;j<i;j++)
            {
                if (ss[i][j]=='2'&&ss[j][i]=='2') num[i][j]=2*n+(++tot);
                if (ss[i][j]=='1') d[i]++;
                if (ss[i][j]=='0') d[j]++;
            }
        }
        int res=0;
        for(int i=0;i<n;i++)
            res+=d[i]*(d[i]-1)/2;
        int s=2*n+tot+1,t=s+1;
        MCMF::init(t,s,t);
        for(int i=0;i<n;i++)
            for(int j=0;j<i;j++)
                if (ss[i][j]=='2')
                {
                    d[i]++; d[j]++;
                    MCMF::AddEdge(i,i+n,1,d[i]-1);
                    MCMF::AddEdge(j,j+n,1,d[j]-1);
                    MCMF::AddEdge(i+n,num[i][j],1,0);
                    MCMF::AddEdge(j+n,num[i][j],1,0);
                    MCMF::AddEdge(num[i][j],t,1,0);
                }
        for(int i=0;i<n;i++)
            MCMF::AddEdge(s,i,INF,0);
        int flow,cost;
        MCMF::Min_cost(flow,cost);
        cost=(cost+res)*(n-3)*8;
        printf("%d\n",n*(n-1)*(n-2)*(n-3)-cost);
    }
    return 0;
}