演算法與資料結構之排序演算法的相關知識,簡單易懂。
一、 氣泡排序
1) 概要
本章介紹排序演算法中的氣泡排序,重點講解氣泡排序的思想。
目錄
1. 氣泡排序介紹
2. 氣泡排序圖文說明
3. 氣泡排序的時間複雜度和穩定性
4. 氣泡排序實現
4.1 氣泡排序C實現
4.2 氣泡排序C++實現
4.3 氣泡排序Java實現
2) 氣泡排序介紹
氣泡排序(Bubble Sort),又被稱為氣泡排序或泡沫排序。
它是一種較簡單的排序演算法。它會遍歷若干次要排序的數列,每次遍歷時,它都會從前往後依次的比較相鄰兩個數的大小;如果前者比後者大,則交換它們的位置。這樣,一次遍歷之後,最大的元素就在數列的末尾!採用相同的方法再次遍歷時,第二大的元素就被排列在最大元素之前。重複此操作,直到整個數列都有序為止!
3) 氣泡排序圖文說明
氣泡排序C實現一
void bubble_sort1(int a[], int n)
{
int i,j;
for (i=n-1; i>0; i--)
{
// 將a[0...i]中最大的資料放在末尾
for (j=0; j<i; j++)
{
if (a[j] > a[j+1])
swap(a[j], a[j+1]);
}
}
}
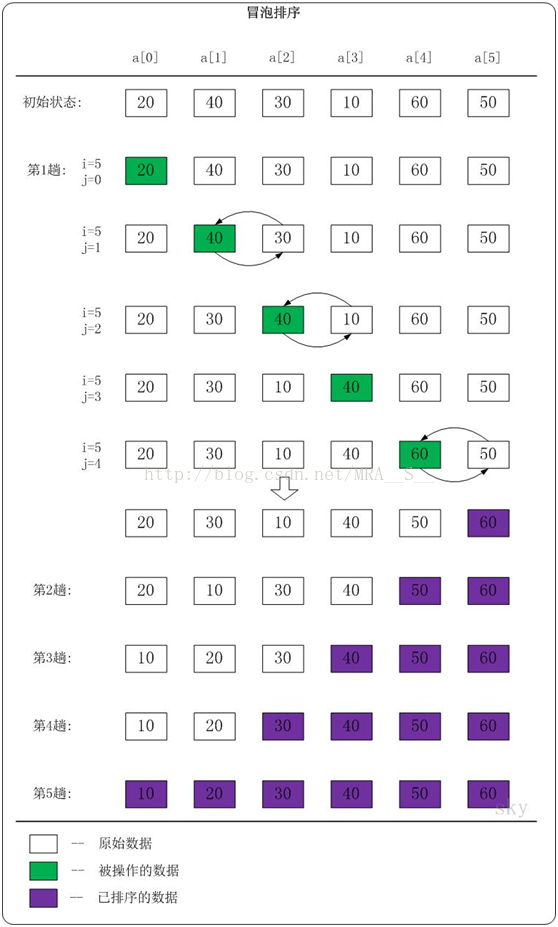
下面以數列{20,40,30,10,60,50}為例,演示它的氣泡排序過程(如下圖)。
我們先分析第1趟排序
當i=5,j=0時,a[0]<a[1]。此時,不做任何處理!
當i=5,j=1時,a[1]>a[2]。此時,交換a[1]和a[2]的值;交換之後,a[1]=30,a[2]=40。
當i=5,j=2時,a[2]>a[3]。此時,交換a[2]和a[3]的值;交換之後,a[2]=10,a[3]=40。
當i=5,j=3時,a[3]<a[4]。此時,不做任何處理!
當i=5,j=4時,a[4]>a[5]。此時,交換a[4]和a[5]的值;交換之後,a[4]=50,a[3]=60。
於是,第1趟排序完之後,數列{20,40,30,10,60,50}變成了{20,30,10,40,50,60}。此時,數列末尾的值最大。
根據這種方法:
第2趟排序完之後,數列中a[5...6]是有序的。
第3趟排序完之後,數列中a[4...6]是有序的。
第4趟排序完之後,數列中a[3...6]是有序的。
第5趟排序完之後,數列中a[1...6]是有序的。
第5趟排序之後,整個數列也就是有序的了。
氣泡排序C實現二
觀察上面氣泡排序的流程圖,第3趟排序之後,資料已經是有序的了;第4趟和第5趟並沒有進行資料交換。
下面我們對氣泡排序進行優化,使它效率更高一些:新增一個標記,如果一趟遍歷中發生了交換,則標記為true,否則為false。如果某一趟沒有發生交換,說明排序已經完成!
void bubble_sort2(int a[], int n)
{
int i,j;
int flag; // 標記
for (i=n-1; i>0; i--)
{
flag = 0; // 初始化標記為0
// 將a[0...i]中最大的資料放在末尾
for (j=0; j<i; j++)
{
if (a[j] > a[j+1])
{
swap(a[j], a[j+1]);
flag = 1; // 若發生交換,則設標記為1
}
}
if (flag==0)
break; // 若沒發生交換,則說明數列已有序。
}
}
4) 氣泡排序的時間複雜度和穩定性
氣泡排序時間複雜度
氣泡排序的時間複雜度是O(N2)。
假設被排序的數列中有N個數。遍歷一趟的時間複雜度是O(N),需要遍歷多少次呢?N-1次!因此,氣泡排序的時間複雜度是O(N2)。
氣泡排序穩定性
氣泡排序是穩定的演算法,它滿足穩定演算法的定義。
演算法穩定性 -- 假設在數列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;並且排序之後,a[i]仍然在a[j]前面。則這個排序演算法是穩定的!
5) 氣泡排序實現
實現程式碼(BubbleSort.java)
/**
* 氣泡排序:Java
*
*@author skywang
*@date 2014/03/11
*/
public class BubbleSort {
/*
* 氣泡排序
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void bubbleSort1(int[] a, int n) {
int i,j;
for (i=n-1; i>0; i--) {
// 將a[0...i]中最大的資料放在末尾
for (j=0; j<i; j++) {
if (a[j] > a[j+1]) {
// 交換a[j]和a[j+1]
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
}
}
}
}
/*
* 氣泡排序(改進版)
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void bubbleSort2(int[] a, int n) {
int i,j;
int flag; // 標記
for (i=n-1; i>0; i--) {
flag = 0; // 初始化標記為0
// 將a[0...i]中最大的資料放在末尾
for (j=0; j<i; j++) {
if (a[j] > a[j+1]) {
// 交換a[j]和a[j+1]
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = 1; // 若發生交換,則設標記為1
}
}
if (flag==0)
break; // 若沒發生交換,則說明數列已有序。
}
}
public static void main(String[] args) {
int i;
int[] a = {20,40,30,10,60,50};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
bubbleSort1(a, a.length);
//bubbleSort2(a, a.length);
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
上面3種實現的原理和輸出結果都是一樣的。下面是它們的輸出結果:
before sort:20 40 30 10 60 50
after sort:10 20 30 40 50 60
二、 快速排序
1) 概要
本章介紹排序演算法中的快速排序。
目錄
1. 快速排序介紹
2. 快速排序圖文說明
3. 快速排序的時間複雜度和穩定性
4. 快速排序實現
4.1 快速排序C實現
4.2 快速排序C++實現
4.3 快速排序Java實現
2) 快速排序介紹
快速排序(Quick Sort)使用分治法策略。
它的基本思想是:選擇一個基準數,通過一趟排序將要排序的資料分割成獨立的兩部分;其中一部分的所有資料都比另外一部分的所有資料都要小。然後,再按此方法對這兩部分資料分別進行快速排序,整個排序過程可以遞迴進行,以此達到整個資料變成有序序列。
快速排序流程:
(1) 從數列中挑出一個基準值。
(2) 將所有比基準值小的擺放在基準前面,所有比基準值大的擺在基準的後面(相同的數可以到任一邊);在這個分割槽退出之後,該基準就處於數列的中間位置。
(3) 遞迴地把"基準值前面的子數列"和"基準值後面的子數列"進行排序。
3) 快速排序圖文說明
快速排序程式碼
/*
* 快速排序
*
* 引數說明:
* a-- 待排序的陣列
* l-- 陣列的左邊界(例如,從起始位置開始排序,則l=0)
* r-- 陣列的右邊界(例如,排序截至到陣列末尾,則r=a.length-1)
*/
void quick_sort(int a[], int l, int r)
{
if (l < r)
{
int i,j,x;
i = l;
j = r;
x = a[i];
while (i < j)
{
while(i < j && a[j] > x)
j--; // 從右向左找第一個小於x的數
if(i < j)
a[i++] = a[j];
while(i < j && a[i] < x)
i++; // 從左向右找第一個大於x的數
if(i < j)
a[j--] = a[i];
}
a[i] = x;
quick_sort(a, l, i-1); /* 遞迴呼叫 */
quick_sort(a, i+1, r); /* 遞迴呼叫 */
}
}
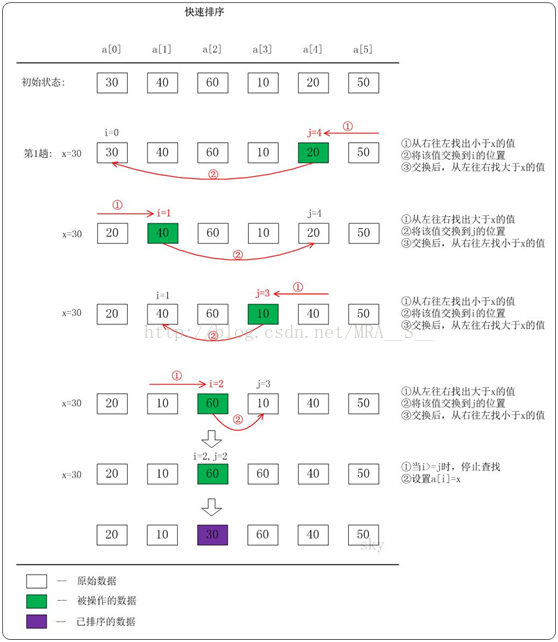
下面以數列a={30,40,60,10,20,50}為例,演示它的快速排序過程(如下圖)。
上圖只是給出了第1趟快速排序的流程。在第1趟中,設定x=a[i],即x=30。
(01) 從"右 --> 左"查詢小於x的數:找到滿足條件的數a[j]=20,此時j=4;然後將a[j]賦值a[i],此時i=0;接著從左往右遍歷。
(02) 從"左 --> 右"查詢大於x的數:找到滿足條件的數a[i]=40,此時i=1;然後將a[i]賦值a[j],此時j=4;接著從右往左遍歷。
(03) 從"右 --> 左"查詢小於x的數:找到滿足條件的數a[j]=10,此時j=3;然後將a[j]賦值a[i],此時i=1;接著從左往右遍歷。
(04) 從"左 --> 右"查詢大於x的數:找到滿足條件的數a[i]=60,此時i=2;然後將a[i]賦值a[j],此時j=3;接著從右往左遍歷。
(05) 從"右 --> 左"查詢小於x的數:沒有找到滿足條件的數。當i>=j時,停止查詢;然後將x賦值給a[i]。此趟遍歷結束!
按照同樣的方法,對子數列進行遞迴遍歷。最後得到有序陣列!
4) 快速排序的時間複雜度和穩定性
快速排序穩定性
快速排序是不穩定的演算法,它不滿足穩定演算法的定義。
演算法穩定性 -- 假設在數列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;並且排序之後,a[i]仍然在a[j]前面。則這個排序演算法是穩定的!
快速排序時間複雜度
快速排序的時間複雜度在最壞情況下是O(N2),平均的時間複雜度是O(N*lgN)。
這句話很好理解:假設被排序的數列中有N個數。遍歷一次的時間複雜度是O(N),需要遍歷多少次呢?至少lg(N+1)次,最多N次。
(01) 為什麼最少是lg(N+1)次?快速排序是採用的分治法進行遍歷的,我們將它看作一棵二叉樹,它需要遍歷的次數就是二叉樹的深度,而根據完全二叉樹的定義,它的深度至少是lg(N+1)。因此,快速排序的遍歷次數最少是lg(N+1)次。
(02) 為什麼最多是N次?這個應該非常簡單,還是將快速排序看作一棵二叉樹,它的深度最大是N。因此,快讀排序的遍歷次數最多是N次。
5) 快速排序實現
實現程式碼(QuickSort.java)
/**
* 快速排序:Java
*
*@author skywang
*@date 2014/03/11
*/
public class QuickSort {
/*
* 快速排序
*
* 引數說明:
* a -- 待排序的陣列
* l -- 陣列的左邊界(例如,從起始位置開始排序,則l=0)
* r -- 陣列的右邊界(例如,排序截至到陣列末尾,則r=a.length-1)
*/
public static void quickSort(int[] a, int l, int r) {
if (l < r) {
int i,j,x;
i = l;
j = r;
x = a[i];
while (i < j) {
while(i < j && a[j]> x)
j--; // 從右向左找第一個小於x的數
if(i < j)
a[i++] = a[j];
while(i < j && a[i]< x)
i++; // 從左向右找第一個大於x的數
if(i < j)
a[j--] = a[i];
}
a[i] = x;
quickSort(a, l, i-1); /* 遞迴呼叫 */
quickSort(a, i+1, r); /* 遞迴呼叫 */
}
}
public static void main(String[] args) {
int i;
int a[] = {30,40,60,10,20,50};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
quickSort(a, 0, a.length-1);
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
上面實現原理和輸出結果都是一樣的。下面是它們的輸出結果:
before sort:30 40 60 10 20 50
after sort:10 20 30 40 50 60
三、 直接插入排序
1) 概要
本章介紹排序演算法中的直接插入排序。內容包括:
1. 直接插入排序介紹
2. 直接插入排序圖文說明
3. 直接插入排序的時間複雜度和穩定性
4. 直接插入排序實現
4.1 直接插入排序C實現
4.2 直接插入排序C++實現
4.3 直接插入排序Java實現
2) 直接插入排序介紹
直接插入排序(Straight Insertion Sort)的基本思想是:把n個待排序的元素看成為一個有序表和一個無序表。開始時有序表中只包含1個元素,無序表中包含有n-1個元素,排序過程中每次從無序表中取出第一個元素,將它插入到有序表中的適當位置,使之成為新的有序表,重複n-1次可完成排序過程。
3) 直接插入排序圖文說明
直接插入排序程式碼
/*
* 直接插入排序
*
* 引數說明:
* a-- 待排序的陣列
* n-- 陣列的長度
*/
void insert_sort(int a[], int n)
{
int i, j, k;
for (i = 1; i < n; i++)
{
//為a[i]在前面的a[0...i-1]有序區間中找一個合適的位置
for (j = i - 1; j >= 0; j--)
if (a[j] < a[i])
break;
//如找到了一個合適的位置
if (j != i - 1)
{
//將比a[i]大的資料向後移
int temp = a[i];
for (k = i - 1; k > j; k--)
a[k + 1] = a[k];
//將a[i]放到正確位置上
a[k + 1] = temp;
}
}
}
下面選取直接插入排序的一箇中間過程對其進行說明。假設{20,30,40,10,60,50}中的前3個數已經排列過,是有序的了;接下來對10進行排列。示意圖如下:
圖中將數列分為有序區和無序區。我們需要做的工作只有兩個:(1)取出無序區中的第1個數,並找出它在有序區對應的位置。(2)將無序區的資料插入到有序區;若有必要的話,則對有序區中的相關資料進行移位。
4) 直接插入排序的時間複雜度和穩定性
直接插入排序時間複雜度
直接插入排序的時間複雜度是O(N2)。
假設被排序的數列中有N個數。遍歷一趟的時間複雜度是O(N),需要遍歷多少次呢?N-1!因此,直接插入排序的時間複雜度是O(N2)。
直接插入排序穩定性
直接插入排序是穩定的演算法,它滿足穩定演算法的定義。
演算法穩定性 -- 假設在數列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;並且排序之後,a[i]仍然在a[j]前面。則這個排序演算法是穩定的!
5) 直接插入排序實現
實現程式碼(InsertSort.java)
/**
* 直接插入排序:Java
*
*@author skywang
*@date 2014/03/11
*/
public class InsertSort {
/*
* 直接插入排序
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void insertSort(int[] a, int n) {
int i, j, k;
for (i = 1; i < n; i++) {
//為a[i]在前面的a[0...i-1]有序區間中找一個合適的位置
for (j = i - 1; j >= 0; j--)
if (a[j] < a[i])
break;
//如找到了一個合適的位置
if (j != i - 1) {
//將比a[i]大的資料向後移
int temp = a[i];
for (k = i - 1; k > j; k--)
a[k + 1] = a[k];
//將a[i]放到正確位置上
a[k + 1] = temp;
}
}
}
public static void main(String[] args) {
int i;
int[] a = {20,40,30,10,60,50};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ",a[i]);
System.out.printf("\n");
insertSort(a, a.length);
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
上面3種實現的原理和輸出結果都是一樣的。下面是它們的輸出結果:
before sort:20 40 30 10 60 50
after sort:10 20 30 40 50 60
四、 希爾排序
1) 概要
本章介紹排序演算法中的希爾排序。內容包括:
1. 希爾排序介紹
2. 希爾排序圖文說明
3. 希爾排序的時間複雜度和穩定性
4. 希爾排序實現
4.1 希爾排序C實現
4.2 希爾排序C++實現
4.3 希爾排序Java實現
2) 希爾排序介紹
希爾排序(Shell Sort)是插入排序的一種,它是針對直接插入排序演算法的改進。該方法又稱縮小增量排序,因DL.Shell於1959年提出而得名。
希爾排序實質上是一種分組插入方法。它的基本思想是:對於n個待排序的數列,取一個小於n的整數gap(gap被稱為步長)將待排序元素分成若干個組子序列,所有距離為gap的倍數的記錄放在同一個組中;然後,對各組內的元素進行直接插入排序。 這一趟排序完成之後,每一個組的元素都是有序的。然後減小gap的值,並重復執行上述的分組和排序。重複這樣的操作,當gap=1時,整個數列就是有序的。
3) 希爾排序圖文說明
希爾排序程式碼(一)
/*
* 希爾排序
*
* 引數說明:
* a-- 待排序的陣列
* n-- 陣列的長度
*/
void shell_sort1(int a[], int n)
{
int i,j,gap;
// gap為步長,每次減為原來的一半。
for (gap = n / 2; gap > 0; gap /= 2)
{
// 共gap個組,對每一組都執行直接插入排序
for (i = 0 ;i < gap; i++)
{
for (j = i + gap; j < n; j += gap)
{
// 如果a[j]< a[j-gap],則尋找a[j]位置,並將後面資料的位置都後移。
if (a[j] < a[j - gap])
{
int tmp = a[j];
int k = j - gap;
while (k >= 0 &&a[k] > tmp)
{
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = tmp;
}
}
}
}
}
在上面的希爾排序中,首先要選取步長gap的值。選取了gap之後,就將數列分成了gap個組,對於每一個組都執行直接插入排序。在排序完所有的組之後,將gap的值減半;繼續對數列進行分組,然後進行排序。重複這樣的操作,直到gap<0為止。此時,數列也就是有序的了。
為了便於觀察,我們將希爾排序中的直接插入排序獨立出來,得到程式碼(二)。
希爾排序程式碼(二)
/*
* 對希爾排序中的單個組進行排序
*
* 引數說明:
* a-- 待排序的陣列
* n-- 陣列總的長度
* i-- 組的起始位置
* gap -- 組的步長
*
* 組是"從i開始,將相隔gap長度的數都取出"所組成的!
*/
void group_sort(int a[], int n, int i,intgap)
{
int j;
for (j = i + gap; j < n; j += gap)
{
// 如果a[j] < a[j-gap],則尋找a[j]位置,並將後面資料的位置都後移。
if (a[j] < a[j - gap])
{
int tmp = a[j];
int k = j - gap;
while (k >= 0 && a[k] > tmp)
{
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = tmp;
}
}
}
/*
* 希爾排序
*
* 引數說明:
* a-- 待排序的陣列
* n-- 陣列的長度
*/
void shell_sort2(int a[], int n)
{
int i,gap;
// gap為步長,每次減為原來的一半。
for (gap = n / 2; gap > 0; gap /= 2)
{
// 共gap個組,對每一組都執行直接插入排序
for (i = 0 ;i < gap; i++)
group_sort(a, n, i, gap);
}
}
4) 演示希爾排序過程
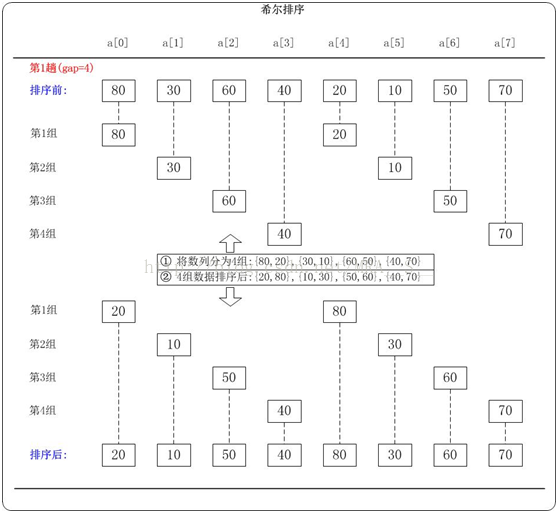
下面以數列{80,30,60,40,20,10,50,70}為例,演示它的希爾排序過程。
第1趟:(gap=4)
當gap=4時,意味著將數列分為4個組: {80,20},{30,10},{60,50},{40,70}。對應數列: {80,30,60,40,20,10,50,70}
對這4個組分別進行排序,排序結果:{20,80},{10,30},{50,60},{40,70}。 對應數列:{20,10,50,40,80,30,60,70}
第2趟:(gap=2)
當gap=2時,意味著將數列分為2個組:{20,50,80,60}, {10,40,30,70}。 對應數列: {20,10,50,40,80,30,60,70}
注意:{20,50,80,60}實際上有兩個有序的數列{20,80}和{50,60}組成。
{10,40,30,70}實際上有兩個有序的數列{10,30}和{40,70}組成。
對這2個組分別進行排序,排序結果:{20,50,60,80},{10,30,40,70}。 對應數列: {20,10,50,30,60,40,80,70}
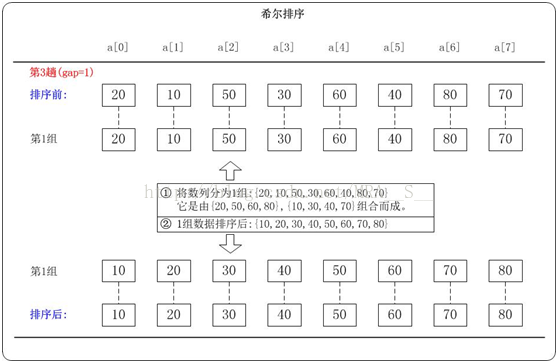
第3趟:(gap=1)
當gap=1時,意味著將數列分為1個組:{20,10,50,30,60,40,80,70}
注意:{20,10,50,30,60,40,80,70}實際上有兩個有序的數列{20,50,60,80}和{10,30,40,70}組成。
對這1個組分別進行排序,排序結果:{10,20,30,40,50,60,70,80}
5) 希爾排序的時間複雜度和穩定性
希爾排序時間複雜度
希爾排序的時間複雜度與增量(即,步長gap)的選取有關。例如,當增量為1時,希爾排序退化成了直接插入排序,此時的時間複雜度為O(N2),而Hibbard增量的希爾排序的時間複雜度為O(N3/2)。
希爾排序穩定性
希爾排序是不穩定的演算法,它滿足穩定演算法的定義。對於相同的兩個數,可能由於分在不同的組中而導致它們的順序發生變化。
演算法穩定性 -- 假設在數列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;並且排序之後,a[i]仍然在a[j]前面。則這個排序演算法是穩定的!
6) 希爾排序實現
實現程式碼(ShellSort.java)
/**
* 希爾排序:Java
*
*@author skywang
*@date 2014/03/11
*/
public class ShellSort {
/**
* 希爾排序
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void shellSort1(int[] a, int n) {
// gap為步長,每次減為原來的一半。
for (int gap = n / 2; gap > 0; gap /= 2) {
// 共gap個組,對每一組都執行直接插入排序
for (int i = 0 ;i < gap; i++) {
for (int j = i + gap; j < n;j += gap) {
// 如果a[j] < a[j-gap],則尋找a[j]位置,並將後面資料的位置都後移。
if (a[j] < a[j - gap]) {
int tmp = a[j];
int k = j - gap;
while (k >= 0&& a[k] > tmp) {
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = tmp;
}
}
}
}
}
/**
* 對希爾排序中的單個組進行排序
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列總的長度
* i -- 組的起始位置
* gap -- 組的步長
*
* 組是"從i開始,將相隔gap長度的數都取出"所組成的!
*/
public static void groupSort(int[] a, int n, int i,int gap) {
for (int j = i + gap; j < n; j += gap) {
// 如果a[j] < a[j-gap],則尋找a[j]位置,並將後面資料的位置都後移。
if (a[j] < a[j - gap]) {
int tmp = a[j];
int k = j - gap;
while (k >= 0 &&a[k] > tmp) {
a[k + gap] = a[k];
k -= gap;
}
a[k + gap] = tmp;
}
}
}
/**
* 希爾排序
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void shellSort2(int[] a, int n) {
// gap為步長,每次減為原來的一半。
for (int gap = n / 2; gap > 0; gap /= 2) {
// 共gap個組,對每一組都執行直接插入排序
for (int i = 0 ;i < gap; i++)
groupSort(a, n, i, gap);
}
}
public static void main(String[] args) {
int i;
int a[] = {80,30,60,40,20,10,50,70};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
shellSort1(a, a.length);
//shellSort2(a, a.length);
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
上面實現的原理和輸出結果都是一樣的。下面是它們的輸出結果:
before sort:80 30 60 40 20 10 50 70
after sort:10 20 30 40 50 60 70 80
五、 選擇排序
1) 概要
本章介紹排序演算法中的選擇排序。
目錄
1. 選擇排序介紹
2. 選擇排序圖文說明
3. 選擇排序的時間複雜度和穩定性
4. 選擇排序實現
4.1 選擇排序C實現
4.2 選擇排序C++實現
4.3 選擇排序Java實現
2) 選擇排序介紹
選擇排序(Selection sort)是一種簡單直觀的排序演算法。
它的基本思想是:首先在未排序的數列中找到最小(or最大)元素,然後將其存放到數列的起始位置;接著,再從剩餘未排序的元素中繼續尋找最小(or最大)元素,然後放到已排序序列的末尾。以此類推,直到所有元素均排序完畢。
3) 選擇排序圖文說明
選擇排序程式碼
/*
* 選擇排序
*
* 引數說明:
* a-- 待排序的陣列
* n-- 陣列的長度
*/
void select_sort(int a[], int n)
{
int i; // 有序區的末尾位置
intj; // 無序區的起始位置
int min; // 無序區中最小元素位置
for(i=0; i<n; i++)
{
min=i;
// 找出"a[i+1] ... a[n]"之間的最小元素,並賦值給min。
for(j=i+1; j<n; j++)
{
if(a[j] < a[min])
min=j;
}
// 若min!=i,則交換 a[i] 和 a[min]。
// 交換之後,保證了a[0] ... a[i] 之間的元素是有序的。
if(min != i)
swap(a[i], a[min]);
}
}
下面以數列{20,40,30,10,60,50}為例,演示它的選擇排序過程(如下圖)。
排序流程
第1趟:i=0。找出a[1...5]中的最小值a[3]=10,然後將a[0]和a[3]互換。 數列變化:20,40,30,10,60,50-- > 10,40,30,20,60,50
第2趟:i=1。找出a[2...5]中的最小值a[3]=20,然後將a[1]和a[3]互換。 數列變化:10,40,30,20,60,50-- > 10,20,30,40,60,50
第3趟:i=2。找出a[3...5]中的最小值,由於該最小值大於a[2],該趟不做任何處理。
第4趟:i=3。找出a[4...5]中的最小值,由於該最小值大於a[3],該趟不做任何處理。
第5趟:i=4。交換a[4]和a[5]的資料。 數列變化:10,20,30,40,60,50-- > 10,20,30,40,50,60
4) 選擇排序的時間複雜度和穩定性
選擇排序時間複雜度
選擇排序的時間複雜度是O(N2)。
假設被排序的數列中有N個數。遍歷一趟的時間複雜度是O(N),需要遍歷多少次呢?N-1!因此,選擇排序的時間複雜度是O(N2)。
選擇排序穩定性
選擇排序是穩定的演算法,它滿足穩定演算法的定義。
演算法穩定性 -- 假設在數列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;並且排序之後,a[i]仍然在a[j]前面。則這個排序演算法是穩定的!
5) 選擇排序實現
實現程式碼(SelectSort.java)
/**
* 選擇排序:Java
*
*@author skywang
*@date 2014/03/11
*/
public class SelectSort {
/*
* 選擇排序
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void selectSort(int[] a, int n) {
int i; // 有序區的末尾位置
int j; // 無序區的起始位置
int min; // 無序區中最小元素位置
for(i=0; i<n; i++) {
min=i;
// 找出"a[i+1] ... a[n]"之間的最小元素,並賦值給min。
for(j=i+1; j<n; j++) {
if(a[j] < a[min])
min=j;
}
// 若min!=i,則交換 a[i] 和 a[min]。
// 交換之後,保證了a[0] ... a[i] 之間的元素是有序的。
if(min != i) {
int tmp = a[i];
a[i] = a[min];
a[min] = tmp;
}
}
}
public static void main(String[] args) {
int i;
int[] a = {20,40,30,10,60,50};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
selectSort(a, a.length);
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
上面3種實現的原理和輸出結果都是一樣的。下面是它們的輸出結果:
before sort:20 40 30 10 60 50
after sort:10 20 30 40 50 60
六、 堆排序
1) 概要
本章介紹排序演算法中的堆排序。
目錄
1. 堆排序介紹
2. 堆排序圖文說明
3. 堆排序的時間複雜度和穩定性
4. 堆排序實現
4.1 堆排序C實現
4.2 堆排序C++實現
4.3 堆排序Java實現
2) 堆排序介紹
堆排序(Heap Sort)是指利用堆這種資料結構所設計的一種排序演算法。
因此,學習堆排序之前,有必要了解堆!若讀者不熟悉堆,建議先了解堆(建議可以通過二叉堆,左傾堆,斜堆,二項堆或斐波那契堆等文章進行了解),然後再來學習本章。
我們知道,堆分為"最大堆"和"最小堆"。最大堆通常被用來進行"升序"排序,而最小堆通常被用來進行"降序"排序。
鑑於最大堆和最小堆是對稱關係,理解其中一種即可。本文將對最大堆實現的升序排序進行詳細說明。
最大堆進行升序排序的基本思想:
① 初始化堆:將數列a[1...n]構造成最大堆。
② 交換資料:將a[1]和a[n]交換,使a[n]是a[1...n]中的最大值;然後將a[1...n-1]重新調整為最大堆。 接著,將a[1]和a[n-1]交換,使a[n-1]是a[1...n-1]中的最大值;然後將a[1...n-2]重新調整為最大值。 依次類推,直到整個數列都是有序的。
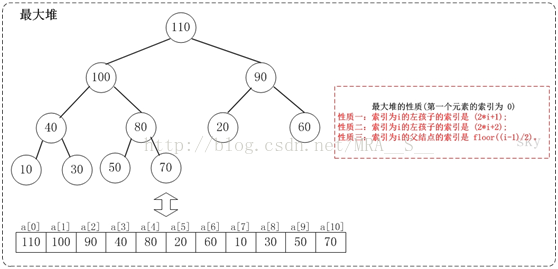
下面,通過圖文來解析堆排序的實現過程。注意實現中用到了"陣列實現的二叉堆的性質"。
在第一個元素的索引為 0 的情形中:
性質一:索引為i的左孩子的索引是(2*i+1);
性質二:索引為i的左孩子的索引是(2*i+2);
性質三:索引為i的父結點的索引是floor((i-1)/2);
例如,對於最大堆{110,100,90,40,80,20,60,10,30,50,70}而言:索引為0的左孩子的所有是1;索引為0的右孩子是2;索引為8的父節點是3。
3) 堆排序圖文說明
堆排序(升序)程式碼
/*
* (最大)堆的向下調整演算法
*
* 注:陣列實現的堆中,第N個節點的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 其中,N為陣列下標索引值,如陣列中第1個數對應的N為0。
*
* 引數說明:
* a-- 待排序的陣列
* start -- 被下調節點的起始位置(一般為0,表示從第1個開始)
* end -- 截至範圍(一般為陣列中最後一個元素的索引)
*/
void maxheap_down(int a[], int start, intend)
{
int c = start; // 當前(current)節點的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 當前(current)節點的大小
for (; l <= end; c=l,l=2*l+1)
{
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] < a[l+1])
l++; // 左右兩孩子中選擇較大者,即m_heap[l+1]
if (tmp >= a[l])
break; // 調整結束
else // 交換值
{
a[c] = a[l];
a[l]= tmp;
}
}
}
/*
* 堆排序(從小到大)
*
* 引數說明:
* a-- 待排序的陣列
* n-- 陣列的長度
*/
void heap_sort_asc(int a[], int n)
{
int i;
// 從(n/2-1) --> 0逐次遍歷。遍歷之後,得到的陣列實際上是一個(最大)二叉堆。
for (i = n / 2 - 1; i >= 0; i--)
maxheap_down(a, i, n-1);
// 從最後一個元素開始對序列進行調整,不斷的縮小調整的範圍直到第一個元素
for (i = n - 1; i > 0; i--)
{
// 交換a[0]和a[i]。交換後,a[i]是a[0...i]中最大的。
swap(a[0], a[i]);
// 調整a[0...i-1],使得a[0...i-1]仍然是一個最大堆。
// 即,保證a[i-1]是a[0...i-1]中的最大值。
maxheap_down(a, 0, i-1);
}
}
heap_sort_asc(a, n)的作用是:對陣列a進行升序排序;其中,a是陣列,n是陣列長度。
heap_sort_asc(a, n)的操作分為兩部分:初始化堆 和 交換資料。
maxheap_down(a, start, end)是最大堆的向下調整演算法。
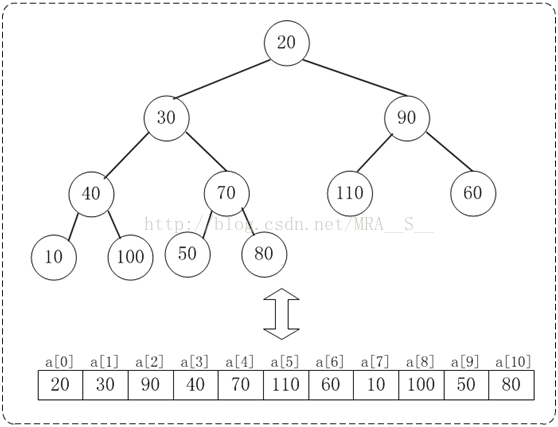
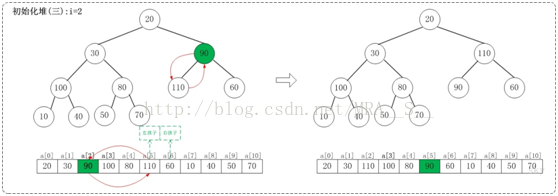
下面演示heap_sort_asc(a, n)對a={20,30,90,40,70,110,60,10,100,50,80}, n=11進行堆排序過程。下面是陣列a對應的初始化結構:
1 初始化堆
在堆排序演算法中,首先要將待排序的陣列轉化成二叉堆。
下面演示將陣列{20,30,90,40,70,110,60,10,100,50,80}轉換為最大堆{110,100,90,40,80,20,60,10,30,50,70}的步驟。
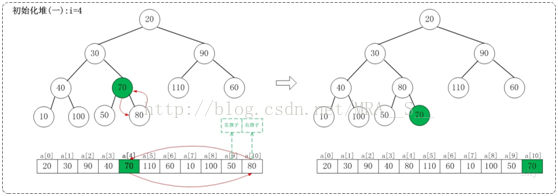
1.1 i=11/2-1,即i=4
上面是maxheap_down(a, 4, 9)調整過程。maxheap_down(a, 4, 9)的作用是將a[4...9]進行下調;a[4]的左孩子是a[9],右孩子是a[10]。調整時,選擇左右孩子中較大的一個(即a[10])和a[4]交換。
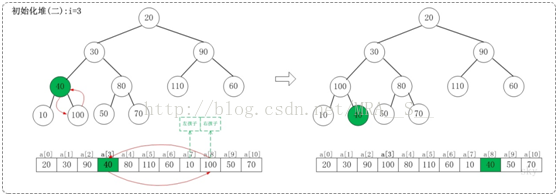
1.2 i=3
上面是maxheap_down(a, 3, 9)調整過程。maxheap_down(a, 3, 9)的作用是將a[3...9]進行下調;a[3]的左孩子是a[7],右孩子是a[8]。調整時,選擇左右孩子中較大的一個(即a[8])和a[4]交換。
1.3 i=2
上面是maxheap_down(a, 2, 9)調整過程。maxheap_down(a, 2, 9)的作用是將a[2...9]進行下調;a[2]的左孩子是a[5],右孩子是a[6]。調整時,選擇左右孩子中較大的一個(即a[5])和a[2]交換。
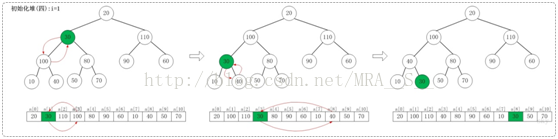
1.4 i=1
上面是maxheap_down(a, 1, 9)調整過程。maxheap_down(a, 1, 9)的作用是將a[1...9]進行下調;a[1]的左孩子是a[3],右孩子是a[4]。調整時,選擇左右孩子中較大的一個(即a[3])和a[1]交換。交換之後,a[3]為30,它比它的右孩子a[8]要大,接著,再將它們交換。
1.5 i=0
上面是maxheap_down(a, 0, 9)調整過程。maxheap_down(a, 0, 9)的作用是將a[0...9]進行下調;a[0]的左孩子是a[1],右孩子是a[2]。調整時,選擇左右孩子中較大的一個(即a[2])和a[0]交換。交換之後,a[2]為20,它比它的左右孩子要大,選擇較大的孩子(即左孩子)和a[2]交換。
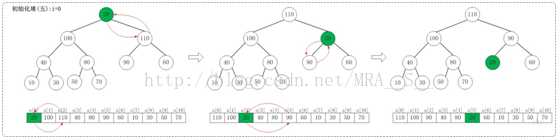
調整完畢,就得到了最大堆。此時,陣列{20,30,90,40,70,110,60,10,100,50,80}也就變成了{110,100,90,40,80,20,60,10,30,50,70}。
第2部分 交換資料
在將陣列轉換成最大堆之後,接著要進行交換資料,從而使陣列成為一個真正的有序陣列。
交換資料部分相對比較簡單,下面僅僅給出將最大值放在陣列末尾的示意圖。
上面是當n=10時,交換資料的示意圖。
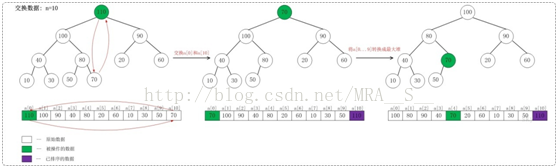
當n=10時,首先交換a[0]和a[10],使得a[10]是a[0...10]之間的最大值;然後,調整a[0...9]使它稱為最大堆。交換之後:a[10]是有序的!
當n=9時, 首先交換a[0]和a[9],使得a[9]是a[0...9]之間的最大值;然後,調整a[0...8]使它稱為最大堆。交換之後:a[9...10]是有序的!
...
依此類推,直到a[0...10]是有序的。
4) 堆排序的時間複雜度和穩定性
堆排序時間複雜度
堆排序的時間複雜度是O(N*lgN)。
假設被排序的數列中有N個數。遍歷一趟的時間複雜度是O(N),需要遍歷多少次呢?
堆排序是採用的二叉堆進行排序的,二叉堆就是一棵二叉樹,它需要遍歷的次數就是二叉樹的深度,而根據完全二叉樹的定義,它的深度至少是lg(N+1)。最多是多少呢?由於二叉堆是完全二叉樹,因此,它的深度最多也不會超過lg(2N)。因此,遍歷一趟的時間複雜度是O(N),而遍歷次數介於lg(N+1)和lg(2N)之間;因此得出它的時間複雜度是O(N*lgN)。
堆排序穩定性
堆排序是不穩定的演算法,它不滿足穩定演算法的定義。它在交換資料的時候,是比較父結點和子節點之間的資料,所以,即便是存在兩個數值相等的兄弟節點,它們的相對順序在排序也可能發生變化。
演算法穩定性 -- 假設在數列中存在a[i]=a[j],若在排序之前,a[i]在a[j]前面;並且排序之後,a[i]仍然在a[j]前面。則這個排序演算法是穩定的!
堆排序實現
這實現的原理和輸出結果都是一樣的,每一種實現中都包括了"最大堆對應的升序排列"和"最小堆對應的降序排序"。
5) 實現程式碼(HeapSort.java)
/**
* 堆排序:Java
*
*@author skywang
*@date 2014/03/11
*/
public class HeapSort {
/*
* (最大)堆的向下調整演算法
*
* 注:陣列實現的堆中,第N個節點的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 其中,N為陣列下標索引值,如陣列中第1個數對應的N為0。
*
* 引數說明:
* a -- 待排序的陣列
* start -- 被下調節點的起始位置(一般為0,表示從第1個開始)
* end -- 截至範圍(一般為陣列中最後一個元素的索引)
*/
public static void maxHeapDown(int[] a, int start, int end) {
int c = start; // 當前(current)節點的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 當前(current)節點的大小
for (; l <= end; c=l,l=2*l+1) {
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] < a[l+1])
l++; // 左右兩孩子中選擇較大者,即m_heap[l+1]
if (tmp >= a[l])
break; // 調整結束
else { // 交換值
a[c] = a[l];
a[l]= tmp;
}
}
}
/*
* 堆排序(從小到大)
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void heapSortAsc(int[] a, int n) {
int i,tmp;
// 從(n/2-1) --> 0逐次遍歷。遍歷之後,得到的陣列實際上是一個(最大)二叉堆。
for (i = n / 2 - 1; i >= 0; i--)
maxHeapDown(a, i, n-1);
// 從最後一個元素開始對序列進行調整,不斷的縮小調整的範圍直到第一個元素
for (i = n - 1; i > 0; i--) {
// 交換a[0]和a[i]。交換後,a[i]是a[0...i]中最大的。
tmp = a[0];
a[0] = a[i];
a[i] = tmp;
// 調整a[0...i-1],使得a[0...i-1]仍然是一個最大堆。
// 即,保證a[i-1]是a[0...i-1]中的最大值。
maxHeapDown(a, 0, i-1);
}
}
/*
* (最小)堆的向下調整演算法
*
* 注:陣列實現的堆中,第N個節點的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
* 其中,N為陣列下標索引值,如陣列中第1個數對應的N為0。
*
* 引數說明:
* a -- 待排序的陣列
* start -- 被下調節點的起始位置(一般為0,表示從第1個開始)
* end -- 截至範圍(一般為陣列中最後一個元素的索引)
*/
public static void minHeapDown(int[] a, int start, int end) {
int c = start; // 當前(current)節點的位置
int l = 2*c + 1; // 左(left)孩子的位置
int tmp = a[c]; // 當前(current)節點的大小
for (; l <= end; c=l,l=2*l+1) {
// "l"是左孩子,"l+1"是右孩子
if ( l < end && a[l] > a[l+1])
l++; // 左右兩孩子中選擇較小者
if (tmp <= a[l])
break; // 調整結束
else { // 交換值
a[c] = a[l];
a[l]= tmp;
}
}
}
/*
* 堆排序(從大到小)
*
* 引數說明:
* a -- 待排序的陣列
* n -- 陣列的長度
*/
public static void heapSortDesc(int[] a, int n) {
int i,tmp;
// 從(n/2-1) --> 0逐次遍歷每。遍歷之後,得到的陣列實際上是一個最小堆。
for (i = n / 2 - 1; i >= 0; i--)
minHeapDown(a, i, n-1);
// 從最後一個元素開始對序列進行調整,不斷的縮小調整的範圍直到第一個元素
for (i = n - 1; i > 0; i--) {
// 交換a[0]和a[i]。交換後,a[i]是a[0...i]中最小的。
tmp = a[0];
a[0] = a[i];
a[i] = tmp;
// 調整a[0...i-1],使得a[0...i-1]仍然是一個最小堆。
// 即,保證a[i-1]是a[0...i-1]中的最小值。
minHeapDown(a, 0, i-1);
}
}
public static void main(String[] args) {
int i;
int a[] = {20,30,90,40,70,110,60,10,100,50,80};
System.out.printf("before sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
heapSortAsc(a, a.length); // 升序排列
//heapSortDesc(a, a.length); // 降序排列
System.out.printf("after sort:");
for (i=0; i<a.length; i++)
System.out.printf("%d ", a[i]);
System.out.printf("\n");
}
}
它們的輸出結果:
before sort:20 30 90 40 70 110 60 10 100 5080
after sort:10 20 30 40 50 60 70 80 90 100 110
七、 歸併排序
1) 概要
本章介紹排序演算法中的歸併排序。內容包括:
1. 歸併排序介紹
2. 歸併排序圖文說明
3. 歸併排序的時間複雜度和穩定性
4. 歸併排序實現
歸併排序介紹
將兩個的有序數列合併成一個有序數列,我們稱之為"歸併"。
歸併排序(Merge Sort)就是利用歸併思想對數列進行排序。根據具體的實現,歸併排序包括"從上往下"和"從下往上"2種方式。
1. 從下往上的歸併排序:將待排序的數列分成若干個長度為1的子數列,然後將這些數列兩兩合併;得到若干個長度為2的有序數列,再將這些數列兩兩合併;得到若干個長度為4的有序數列,再將它們兩兩合併;直接合併成一個數列為止。這樣就得到了我們想要的排序結果。(參考下面的圖片)
2. 從上往下的歸併排序:它與"從下往上"在排序上是反方向的。它基本包括3步:
① 分解 -- 將當前區間一分為二,即求分裂點 mid = (low + high)/2;
② 求解 -- 遞迴地對兩個子區間a[low...mid]和 a[mid+1...high]進行歸併排序。遞迴的終結條件是子區間長度為1。
③ 合併 -- 將已排序的兩個子區間a[low...mid]和 a[mid+1...high]歸併為一個有序的區間a[low...high]。
下面的圖片很清晰的反映了"從下往上"和"從上往下"的歸併排序的區別。
2) 歸併排序圖文說明
歸併排序(從上往下)程式碼
/*
* 將一個數組中的兩個相鄰有序區間合併成一個
*
* 引數說明:
* a-- 包含兩個有序區間的陣列
* start -- 第1個有序區間的起始地址。
* mid -- 第1個有序區間的結束地址。也是第2個有序區間的起始地址。
* end -- 第2個有序區間的結束地址。
*/
void merge(int a[], int start, int mid, intend)
{
int *tmp = (int *)malloc((end-start+1)*sizeof(int)); // tmp是彙總2個有序區的臨時區域
int i = start; // 第1個有序區的索引
int j = mid + 1; // 第2個有序區的索引
int k = 0; // 臨時區域的索引
while(i <= mid && j <= end)
{
if (a[i] <= a[j])
tmp[k++] = a[i++];
else
tmp[k++] = a[j++];
}
while(i <= mid)
tmp[k++] = a[i++];
while(j <= end)
tmp[k++] = a[j++];
// 將排序後的元素,全部都整合到陣列a中。
for (i = 0; i < k; i++)
a[start + i] = tmp[i];
free(tmp);
}
/*
* 歸併排序(從上往下)
*
* 引數說明:
* a-- 待排序的陣列
* start -- 陣列的起始地址
* endi -- 陣列的結束地址
*/
void merge_sort_up2down(int a[], int start,int end)
{
if(a==NULL || start >= end)
return ;
int mid = (end + start)/2;
merge_sort_up2down(a, start, mid); // 遞迴排序a[start...mid]
merge_sort_up2down(a, mid+1, end); // 遞迴排序a[mid+1...end]
// a[start...mid] 和 a[mid...end]是兩個有序空間,
// 將它們排序成一個有序空間a[start...end]
merge(a, start, mid, end);
}
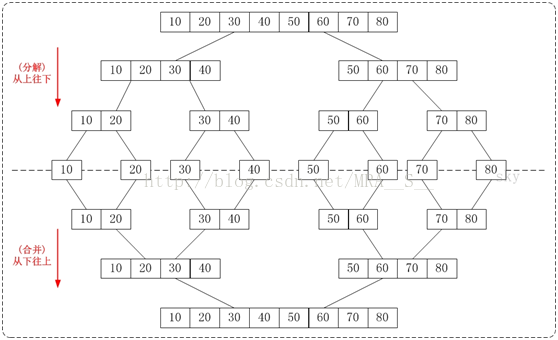
從上往下的歸併排序採用了遞迴的方式實現。它的原理非常簡單,如下圖:
通過"從上往下的歸併排序"來對陣列{80,30,60,40,20,10,50,70}進行排序時:
1. 將陣列{80,30,60,40,20,10,50,70}看作由兩個有序的子陣列{80,30,60,40}和{20,10,50,70}組成。對兩個有序子樹組進行排序即可。
2. 將子陣列{80,30,60,40}看作由兩個有序的子陣列{80,30}和{60,40}組成。
將子陣列{20,10,50,70}看作由兩個有序的子陣列{20,10}和{50,70}組成。
3. 將子陣列{80,30}看作由兩個有序的子陣列{80}和{30}組成。
將子陣列{60,40}看作由兩個有序的子陣列{60}和{40}組成。
將子陣列{20,10}看作由兩個有序的子陣列{20}和{10}組成。
將子陣列{50,70}看作由兩個有序的子陣列{50}和{70}組成。
歸併排序(從下往上)程式碼
/*
* 對陣列a做若干次合併:陣列a的總長度為len,將它分為若干個長度為gap的子陣列;
* 將"每2個相鄰的子陣列" 進行合併排序。
*
* 引數說明:
* a-- 待排序的陣列
* len -- 陣列的長度
* gap -- 子陣列的長度
*/
void merge_groups(int a[], int len, intgap)
{
int i;
int twolen = 2 * gap; // 兩個相鄰的子陣列的長度
// 將"每2個相鄰的子陣列" 進行合併排序。
for(i = 0; i+2*gap-1 < len; i+=(2*gap))
{
merge(a, i, i+gap-1, i+2*gap-1);
}
// 若 i+gap-1 < len-1,則剩餘一個子陣列沒有配對。
// 將該子數組合併到已排序的陣列中。
if ( i+gap-1 < len-1)
{
merge(a, i, i + gap - 1, len - 1);
}
}
/*
* 歸併排序(從下往上)
*
* 引數說明:
* a-- 待排序的陣列
* len -- 陣列的長度
*/
void merge_sort_down2up(int a[], int len)
{
int n;
if (a==NULL || len<=0)
return ;
for(n = 1; n < len; n*=2)
merge_groups(a, len, n);
}
從下往上的歸併排序的思想正好與"從下往上的歸併排序"相反。如下圖:
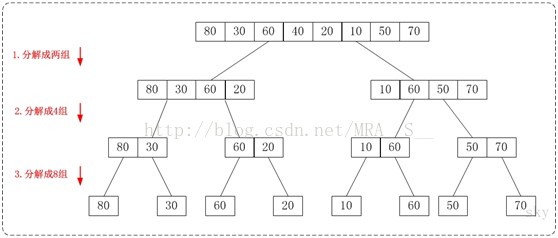
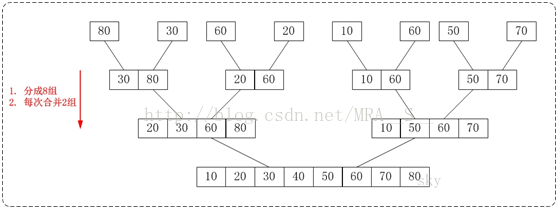
通過"從下往上的歸併排序"來對陣列{80,30,60,40,20,10,50,70}進行排序時:
1. 將陣列{80,30,60,40,20,10,50,70}看作由8個有序的子陣列{80},{30},{60},{40},{20},{10},{50}和{70}組成。
2. 將這8個有序的子數列兩兩合併。得到4個有序的子樹列{30,80},{40,60},{10,20}和{50,70}。
3. 將這4個有序的子數列兩兩合併。得到2個有序的子樹列{30,40,60,80}和{10,20,50,70}。
4. 將這2個有序的子數列兩兩合併。得到1個有序的子樹列{10,20,30,40,50,60,70,80}。
3) 歸併排序的時間複雜度和穩定性
歸併排序時間複雜度
歸併排序的時間複雜度是O(N*lgN)。
假設被排序的數列中有N個數。遍歷一趟的時間複雜度是O(N),需要