JS——排序演算法(一)
一、前言
排序演算法大體可分為兩種:
一種是比較排序,時間複雜度O(nlogn) ~ O(n^2),主要有:氣泡排序,選擇排序,插入排序,歸併排序,堆排序,快速排序等。
另一種是非比較排序,時間複雜度可以達到O(n),主要有:計數排序,基數排序,桶排序等。
下表給出了常見比較排序演算法的效能:

排序演算法穩定性的簡單形式化定義為:如果Ai = Aj,排序前Ai在Aj之前,排序後Ai還在Aj之前,則稱這種排序演算法是穩定的。通俗地講就是保證排序前後兩個相等的數的相對順序不變。
對於不穩定的排序演算法,只要舉出一個例項,即可說明它的不穩定性;而對於穩定的排序演算法,必須對演算法進行分析從而得到穩定的特性。需要注意的是,排序演算法是否為穩定的是由具體演算法決定的,不穩定的演算法在某種條件下可以變為穩定的演算法,而穩定的演算法在某種條件下也可以變為不穩定的演算法。
例如,對於氣泡排序,原本是穩定的排序演算法,如果將記錄交換的條件改成A[i] >= A[i + 1],則兩個相等的記錄就會交換位置,從而變成不穩定的排序演算法。
二、排序演算法
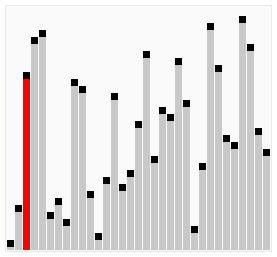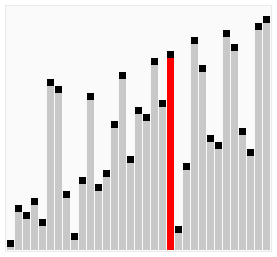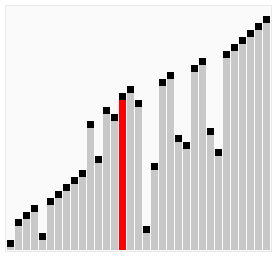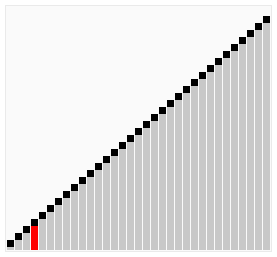
2.1 氣泡排序
氣泡排序演算法的運作如下:
- 比較相鄰的元素,如果前一個比後一個大,就把它們兩個調換位置。
- 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對。這步做完後,最後的元素會是最大的數。
- 針對所有的元素重複以上的步驟,除了最後一個。
- 持續每次對越來越少的元素重複上面的步驟,直到沒有任何一對數字需要比較。
let arr = [6, 65, 3, 1, 98, 87, 42, 24]; console.log(arr); function swap(arr, i, j) { [arr[i],arr[j]] = [arr[j],arr[i]]; } //冒泡演算法排序 function sortBubble(arr) { for(let i = 0; i<arr.length;i++){ for(let j = 0;j<arr.length-1-i;j++){ if(arr[j]>arr[j+1]){ swap(arr,j,j+1); } } } } sortBubble(arr); console.log(arr);
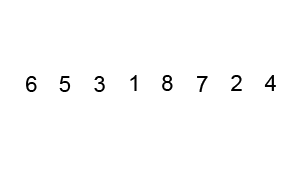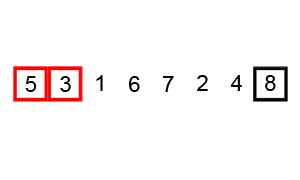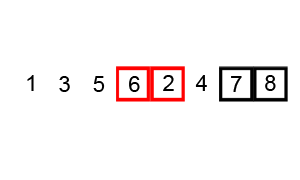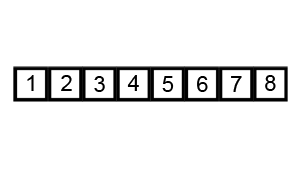
2.2 雞尾酒排序
雞尾酒排序,也叫定向氣泡排序,是氣泡排序的一種改進。此演算法與氣泡排序的不同處在於從低到高然後從高到低,而氣泡排序則僅從低到高去比較序列裡的每個元素。他可以得到比氣泡排序稍微好一點的效能。
let arr = [6, 65, 3, 1, 98, 87, 42, 24]; console.log(arr); function swap(arr, i, j) { [arr[i],arr[j]] = [arr[j],arr[i]]; } //雞尾酒排序 function CocktailSort(arr) { let left = 0; let right = arr.length-1; while (left < right){ for(let i = left; i < right;i++){ if(arr[i]>arr[i+1]){ swap(arr,i,i+1); } } right--; for(let j = right;j>left;j--){ if(arr[j] < arr[j-1]){ swap(arr,j,j-1); } } left++; } } CocktailSort(arr); console.log(arr);
使用雞尾酒排序為一列數字進行排序的過程如圖所示:
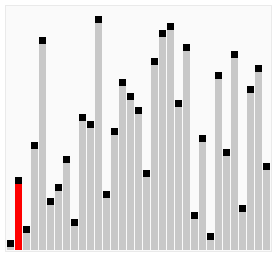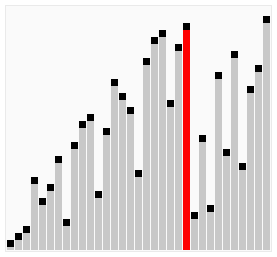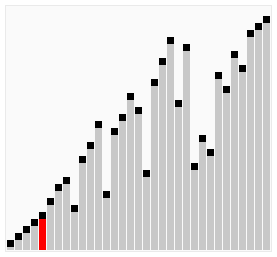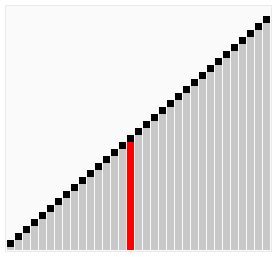
2.3 選擇排序
選擇排序也是一種簡單直觀的方法,以由小到大排序為例:對於初始序列,假設第一個為最小值(下標min),然後依次比較序列中其他數值,遇到比min更小的數值,交換兩者的下標,然後再繼續往下比較,直到與序列的其他值都有比較。然後交換最終帶有min下標和最初帶有min下標的值。這樣就完成一輪比較,找到序列中最小的值。
注意選擇排序與氣泡排序的區別:氣泡排序通過依次交換相鄰兩個順序不合法的元素位置,從而將當前最小(大)元素放到合適的位置;而選擇排序每遍歷一次都記住了當前最小(大)元素的位置,最後僅需一次交換操作即可將其放到合適的位置。
let arr = [6, 65, 3, 1, 98, 87, 42, 24];
console.log(arr);
function swap(arr, i, j) {
[arr[i],arr[j]] = [arr[j],arr[i]];
}
//選擇排序
function selectSort(arr) {
let min;
for(let i = 0; i < arr.length-1;i++){
min = i;
for(let j = i+1;j<arr.length;j++){
if(arr[j] < arr[min]){
min = j;
}
}
if(min !== i){
swap(arr,i,min);
}
}
}
selectSort(arr);
console.log(arr);上述程式碼對序列{ 8, 5, 2, 6, 9, 3, 1, 4, 0, 7 }進行選擇排序的實現過程如圖:
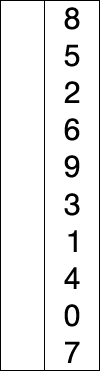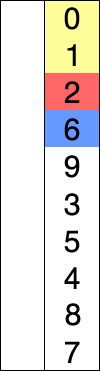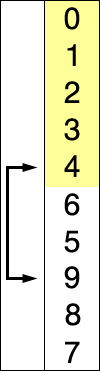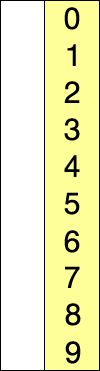
2.4 插入排序
具體演算法描述如下:
- 從第一個元素開始,該元素可以認為已經被排序
- 取出下一個元素,在已經排序的元素序列中從後向前掃描
- 如果該元素(已排序)大於新元素,將該元素移到下一位置
- 重複步驟3,直到找到已排序的元素小於或者等於新元素的位置
- 將新元素插入到該位置後
- 重複步驟2~5
function insertSort(arr) {
for (let i = 1; i < arr.length; i++) {
let get = arr[i];
let j = i - 1;
while (j >= 0 && arr[j] > get) {
//比較之後的動作第一步一定是先移動排好序的數字,然後才是放要插入的get
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = get;//放要插入的get
}
}
insertSort(arr);
console.log(arr);2.5 插入排序的改進:二分插入排序
對於插入排序,如果比較操作的代價比交換操作大的話,可以採用二分查詢法來減少比較操作的次數,我們稱為二分插入排序
function InsertionSortDichotomy(arr) {
for (let i = 1; i < arr.length; i++) {
let get = arr[i];
let left = 0;
let right = i - 1;
//二分法
while (left <= right) {
let mid = parseInt((left + right) / 2);
if (arr[mid] > get) {
right = mid - 1;
} else {
left = mid + 1;
}
}
//console.log(left);
//插入排序
for (let j = i - 1; j >= left; j--) {
arr[j + 1] = arr[j];
}
arr[left] = get;
}
}
InsertionSortDichotomy(arr);
console.log(arr);2.5 插入排序的更高效改進:希爾排序(Shell Sort)
希爾排序,也叫遞減增量排序,是插入排序的一種更高效的改進版本。希爾排序是不穩定的排序演算法。
希爾排序是基於插入排序的以下兩點性質而提出改進方法的:
- 插入排序在對幾乎已經排好序的資料操作時,效率高,即可以達到線性排序的效率
- 但插入排序一般來說是低效的,因為插入排序每次只能將資料移動一位
希爾排序通過將比較的全部元素分為幾個區域來提升插入排序的效能。這樣可以讓一個元素可以一次性地朝最終位置前進一大步。然後演算法再取越來越小的步長進行排序,演算法的最後一步就是普通的插入排序,但是到了這步,需排序的資料幾乎是已排好的了(此時插入排序較快)。
假設有一個很小的資料在一個已按升序排好序的陣列的末端。如果用複雜度為O(n^2)的排序(氣泡排序或直接插入排序),可能會進行n次的比較和交換才能將該資料移至正確位置。而希爾排序會用較大的步長移動資料,所以小資料只需進行少數比較和交換即可到正確位置。
function shellSort(arr) {
let h = 0;
while (h <= arr.length) {
h = h * 3 + 1;//初始化增量(這個增量其實是沒有固定的一個演算法的)
}
while (h >= 1) {
for (let i = h; i < arr.length; i = i + h) {
let j = i - h;
let get = arr[i];
//console.log(get);
while (j >= 0 && arr[j] > get) {
arr[j + h] = arr[j];
j = j - h;
}
arr[j + h] = get;
}
h = (h - 1) / 3;
}
}
shellSort(arr);
console.log(arr);以23, 10, 4, 1的步長序列進行希爾排序:

2.6 歸併排序(遞迴版本)
歸併排序是建立在歸併操作上的一種有效的排序演算法,效率為O(nlogn),1945年由馮·諾伊曼首次提出。遞迴實現的歸併排序是演算法設計中分治策略(Divide and Conquer)的典型應用,我們將一個大問題分割成小問題分別解決,然後用所有小問題的答案來解決整個大問題。
function mergeSort(arr) {
// 設定終止的條件,
if (arr.length < 2) {
return arr;
}
//設立中間值
let middle = parseInt(arr.length / 2);
//第1個和middle個之間為左子列
let left = arr.slice(0, middle);
//第middle+1到最後為右子列
let right = arr.slice(middle);
if (left === "undefined" && right === "undefined") {
return false;
}
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right) {
let result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
//把left的左子樹推出一個,然後push進result數組裡
result.push(left.shift());
} else {
//把right的右子樹推出一個,然後push進result數組裡
result.push(right.shift());
}
}
//經過上面一次迴圈,只能左子列或右子列一個不為空,或者都為空,把剩下的元素都放入新陣列的後面
while (left.length) {
result.push(left.shift());
}
while (right.length) {
result.push(right.shift());
}
return result;
}
console.log(mergeSort(arr));上述程式碼對序列{ 6, 5, 3, 1, 8, 7, 2, 4 }進行歸併排序的例項如下
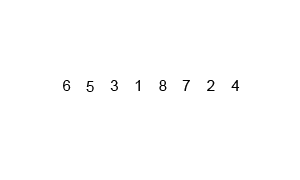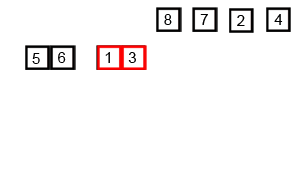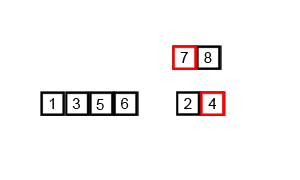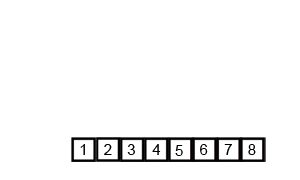
2.7 快速排序
快速排序使用分治策略(Divide and Conquer)來把一個序列分為兩個子序列。步驟為:
- 從序列中挑出一個元素,作為"基準"(pivot).
- 把所有比基準值小的元素放在基準前面,所有比基準值大的元素放在基準的後面(相同的數可以到任一邊),這個稱為分割槽(partition)操作。
- 對每個分割槽遞迴地進行步驟1~2,遞迴的結束條件是序列的大小是0或1,這時整體已經被排好序了。
let quicksort = function(arr) {
if(arr.length <= 1) return arr;
let pivot = Math.floor((arr.length -1)/2);
let val = arr[pivot], less = [], more = [];
arr.splice(pivot, 1);
arr.forEach((e)=>{
e < val ? less.push(e) : more.push(e);
});
return (quicksort(less)).concat([val],quicksort(more));
};
console.log(quicksort(arr));使用快速排序法對一列數字進行排序的過程:

參考文章:
