SVM的matlab實現——CVX工具箱應用

阿新 • • 發佈：2019-02-07

機器學習經典演算法SVM，網上有各種部落格介紹，以及各種語言的原始碼。這裡提供SVM幾種版本的matlab實現，主要目的是熟悉利用CVX來求解凸優化問題。

basic SVM

推導什麼的就不說了，直接搬最後的公式：

minw,b2∥w∥22
s.t.yi(wTxi+b)≥1,i=1,...,Lx_i+b)\ge1,i=1,…,L

然後是程式碼：`

function [ w,b ] = svm_prim_sep( data,labels )
%UNTITLED2 此處顯示有關此函式的摘要
%   Input:
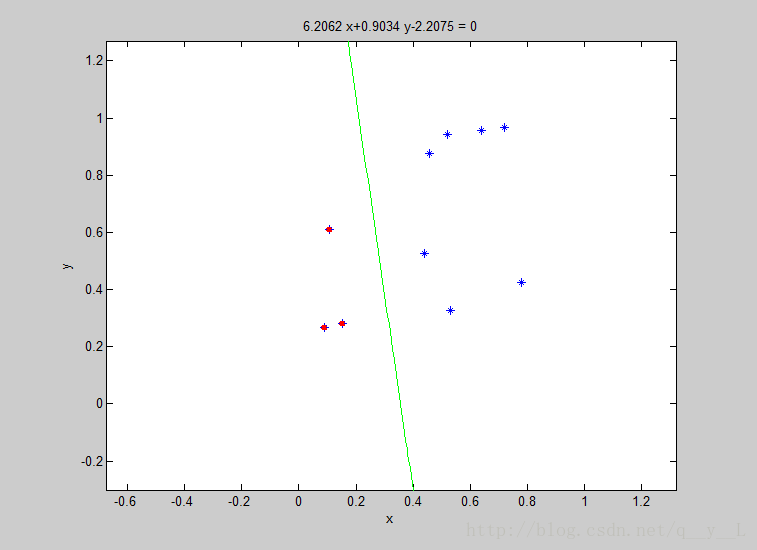
%   data:   num-by-dim matrix .mun is 
 the number of data points,
%   dim is the the dimension of a point
% labels:   num-by-1 vector, specifying the class that each point belongs
% to +1 or -1
%   output:
%   w: dim-by -1 vector ,the mormal dimension of hyperpalne
%   b: a scalar, the bias

[num,dim]=size(data);
cvx_begin
    variables w(dim) b;
    minimize (norm(w));
    subject to 

        labels.*(data*w+b)>=1;
cvx_end
end

然後隨便隨機生成了10個2維樣本，執行結果如下：
這裡寫圖片描述

Soft Margin SVM

Soft Margin SVM
線性不可分的時候，通過引入罰函式（penalty function）來解決，使得分類誤差最小。公式如下：

minw,b,ξi12∥w∥22+C∑i=1Lξi
s.t.yi(wTxi+b)≥1−ξi,i=1,...,L
ξi≥0,i=1,...,L

程式碼依然很簡單：

function [ w,b ] = svm_prim_sep( data,labels )
%UNTITLED2 此處顯示有關此函式的摘要
%   Input:
%   data:   num-by 
-dim matrix .mun is the number of data points,
%   dim is the the dimension of a point
% labels:   num-by-1 vector, specifying the class that each point belongs
% to +1 or -1
%   output:
%   w: dim-by -1 vector ,the mormal dimension of hyperpalne
%   b: a scalar, the bias

[num,dim]=size(data);
cvx_begin
    variables w(dim) b，xi(num);
    minimize (sum(w.^2)/2+C * sum(xi.^2));
    subject to
        labels.* (data * w+b)>=1-xi;
        xi>=0;
cvx_end
end

是不是很簡單？例子以後再給吧。（公式亂碼，請嘗試其它瀏覽器）
未完待續，

SVM的matlab實現——CVX工具箱應用

機器學習經典演算法SVM，網上有各種部落格介紹，以及各種語言的原始碼。這裡提供SVM幾種版本的matlab實現，主要目的是熟悉利用CVX來求解凸優化問題。 basic SVM 推導什麼的就不說了，直接搬最後的公式： minw,b2∥w∥22 s.

機智雲5.0推出IoT套件GoKit4.0 可實現物聯網應用協同開發

人才 day 多個 html 部分包括組件單位 zh-cn 2017年9月19日，全國雙創周期間，在由廣州市青創中心、天英匯、五號空間、機智雲等聯合主辦的眾創五號空間首屆IoT創新嘉年華重頭戲機智雲GODAY2017上，機智雲正式發布了機智雲5.0物聯網開發及雲服務平

使用Xamarin實現跨平臺移動應用開發（轉載）

def acs catch live make asset book -a 開發語言剛在朋友圈看到張善友，轉發的一條分享“使用Xamarin實現跨平臺移動應用開發”，寫的確實很詳細得體，從收費到開源，這段時間xamarin受到不少質疑，如此文h

Vue+Electron實現簡單桌面應用

網上官方文檔決定 lec blank 應用 dirname 瀏覽器 stat 之前一直使用C#編寫桌面應用，也順帶寫一些Web端應用。最近在看node時發現常用的vscode是用electron編寫的，一種想吃螃蟹的念頭就湧了上來。在網上找了找electron的資料，

詳解Nginx搭建多網站實現虛擬主機應用

檢測服務 roo linux 聯網應用程序 top n 行修改 ESS 系統用戶簡介虛擬主機是指在網絡服務器上分出一定的磁盤空間，管理員可以利用此部分空間，放置站點及應用組件，提供必要的數據存放和傳輸功能。虛擬主機，就是把一臺運行在互聯網上的物理服務器劃分成多個“虛擬

邊緣計算對嵌入式系統實現物聯網應用的影響，到底有多大？

引言雲端計算幾年前非常流行，可是當全部應用落地，海量資料湧入雲之後。對應的問題也隨之而來，處理速度慢、時延長，所以邊緣計算成為研究熱點。事實上邊緣計算起源於物聯網應用，它的作用體如今物聯網應用中雲計算的優化設計，其初衷是為了將一些無需上傳到雲的計算留在遠端

應用程序實現對其他應用程式的呼叫

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！

netlink實現驅動和應用層通訊

1、netlink及相關介面說明說到驅動和應用層進行資料通訊，很多人就會想到使用傳統的ioctl，誠然，很多時候應用層呼叫驅動進行引數配置和引數獲取使用的也正是ioctl的方式，但這種方式有一種

CXF實現簡單webservice應用、整合spring釋出到tomcat

前言 Apache CXF提供了用於方便地構建和開發WebService的可靠基礎架構。它允許建立高效能和可擴充套件的服務，可以部署在Tomcat和基於spring的輕量級容器中，也可以部署在更高階的伺服器上，例如Jboss、WebSphere或WebLogic。下面將建立一個簡單的we

Python實現決策樹應用之判斷隱形眼鏡的型別

程式碼模組一、DecisionTreePlot # -*- coding:utf-8 -*- __author__ = 'yangxin_ryan' import matplotlib.pyplot as plt """ 定義文字框和箭頭格式【 sawtooth 波浪方框, rou

邊緣計算對嵌入式系統實現物聯網應用的影響，究竟有多大

雲端計算幾年前非常流行，但是當所有應用落地，海量資料湧入雲之後，相應的問題也隨之而來，處理速度慢、時延長，所以邊緣計算成為研究熱點。其實邊緣計算起源於物聯網應用，它的作用體現在物聯網應用中雲計算的優化設計，其初衷是為了將一些無需上傳到雲的計算留在遠端處理。那麼在嵌入式系統應用中，邊緣計算會起

android多框架實現短視訊應用、3D手勢旋轉、banner控制元件、指南針、智慧管家等應用原始碼

Android精選原始碼 android智慧管家app原始碼 Android高仿拼多多分類列表 Android百度地圖例項詳解之仿摩拜單車APP RecyclerView的LayoutManager搭建流式佈局 Android自定義View分享——一個圓形

銀行卡識別的實現方式及其應用場景

今天一上來，我覺得就可以直切主題。我們來討論下銀行卡識別的實現方式及其應用的場景。銀行卡識別的實現方式分為三種： APP的整合需要將我司的銀行卡識別SDK嵌入到某個APP中去，通過APP呼叫終端的攝像頭，以“掃一掃”的方式獲取銀行卡圖片，再呼叫本地的識別服務，無需聯網

Promise實現ajax簡單應用

Promise是非同步程式設計的一種解決方案。比傳統的解決方案——————回撥函式和事件，Promise更合理和更強大。在ES6規範中，Promise是提供的一個建構函式，可以new Promise（）物件 Promise物件代表一個非同步操作， Promis

ThreadLocal 的實現原理和應用場景

一、ThreadLocal 是什麼 ThreadLocal 是一個執行緒內部的資料儲存類，通過它可以在指定的執行緒中儲存資料，資料儲存以後，只有在指定執行緒中可以獲取到儲存的資料，對於其他執行緒來說則無法獲取到資料可以理解成執行緒本地變數或執行緒本地儲存，Th

關於 C#呼叫一個C/C++dll庫執行時實現多個應用(靜態變數區分) 的解決方法

需求 VS編寫了純C（windows）通訊庫，需要多例項（靜態變數標誌一個例項，達到互相靜態變數不干涉）。當前問題 dll中使用了全域性static的標

使用GPG實現密碼學應用

GPG 1991年，程式設計師Phil Zimmermann為了避開政府的監視，開發了加密軟體PGP。因為這個軟體非常好用，迅速流傳開來成為許多程式設計師的必備工具。但是，它是商業軟不能自由使用。所以，自由軟體基金會決定，開發一個PGP的替代品取名為GnuPG，因此GPG就誕生了。GPG是GNU

AOP的實現原理與應用場景

Spring AOP的實現原理與應用場景作用：在不修改原始碼的情況下，可以實現功能的增強。傳統的縱向體系程式碼複用：橫向抽取機制（AOP思想）： AOP 思想：基於代理思想，對原來目標物件，建立代理物件，在不修改原物件程式碼情況下，通過代理物件，呼叫增強

開源應用 Docker App 加入 CNAB 規範，實現雲原生應用的統一管理

出品丨Docker公司（ID：docker-cn）編譯丨小東每週一、三、五，與您不見不散！ Docker App 是我們在2018 DockerCon 美國大會上簡要介紹的一款新工具。我們一直致力於“Docker APP”的開發，使容器應用程式更易於在不同團隊和不同環境之間共享和管理，我們還將其

SVM的matlab實現——CVX工具箱應用

機器學習經典演算法SVM，網上有各種部落格介紹，以及各種語言的原始碼。 這裡提供SVM幾種版本的matlab實現，主要目的是熟悉利用CVX來求解凸優化問題。

相關推薦

機器學習經典演算法SVM，網上有各種部落格介紹，以及各種語言的原始碼。這裡提供SVM幾種版本的matlab實現，主要目的是熟悉利用CVX來求解凸優化問題。