區塊鏈背後的資訊保安(3)橢圓曲線加解密及簽名演算法的技術原理及其Go語言實現
阿新 • • 發佈:2019-02-07
# 橢圓曲線加解密及簽名演算法的技術原理及其Go語言實現
橢圓曲線加密演算法,即:Elliptic Curve Cryptography,簡稱ECC,是基於橢圓曲線數學理論實現的一種非對稱加密演算法。相比RSA,ECC優勢是可以使用更短的金鑰,來實現與RSA相當或更高的安全。據研究,160位ECC加密安全性相當於1024位RSA加密,210位ECC加密安全性相當於2048位RSA加密。
橢圓曲線在密碼學中的使用,是1985年由Neal Koblitz和Victor Miller分別獨立提出的。
### 橢圓曲線
一般,橢圓曲線可以用如下二元三階方程表示:y² = x³ + ax + b,其中a、b為係數。
如果滿足條件4a³+27b²≠0,則可以基於E(a, b)定義一個群。
其形狀如下:
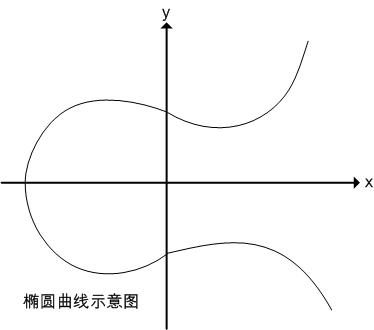
### 定義橢圓曲線的運算規則
橢圓曲線上的運算規則,由如下方式定義:
加法:過曲線上的兩點A、B畫一條直線,找到直線與橢圓曲線的交點,交點關於x軸對稱位置的點,定義為A+B,即為加法。如下圖所示:
A + B = C
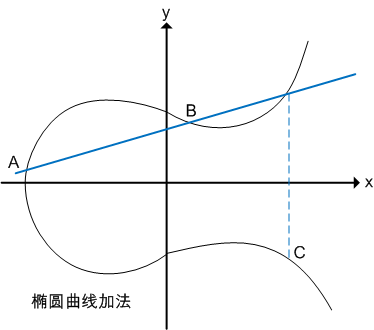
二倍運算:上述方法無法解釋A + A,即兩點重合的情況。因此在這種情況下,將橢圓曲線在A點的切線,與橢圓曲線的交點,交點關於x軸對稱位置的點,定義為A + A,即2A,即為二倍運算。如下圖所示:
A + A = 2A = B
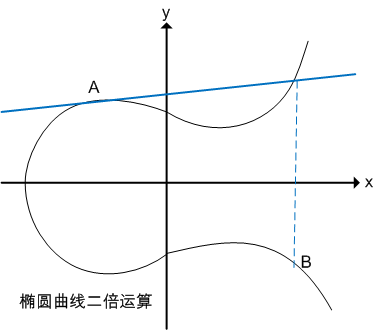
正負取反:將A關於x軸對稱位置的點定義為-A,即橢圓曲線的正負取反運算。如下圖所示:
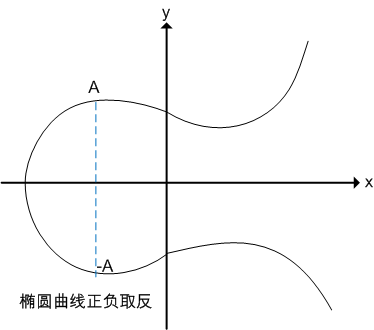
無窮遠點:如果將A與-A相加,過A與-A的直線平行於y軸,可以認為直線與橢圓曲線相交於無窮遠點。如下圖所示:
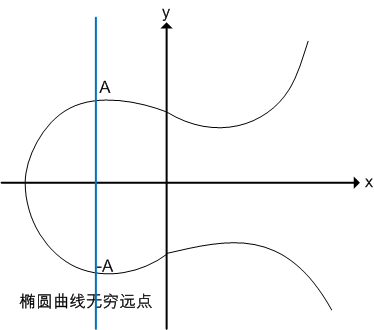
綜上,定義了A+B、2A運算,因此給定橢圓曲線的某一點G,可以求出2G、3G(即G + 2G)、4G......。即:當給定G點時,已知x,求xG點並不困難。反之,已知xG點,求x則非常困難。此即為橢圓曲線加密演算法背後的數學原理。
### 有限域上的橢圓曲線運算
橢圓曲線要形成一條光滑的曲線,要求x,y取值均為實數,即實數域上的橢圓曲線。但橢圓曲線加密演算法,並非使用實數域,而是使用有限域。按數論定義,有限域GF(p)指給定某個質數p,由0、1、2......p-1共p個元素組成的整數集合中定義的加減乘除運算。
假設橢圓曲線為y² = x³ + x + 1,其在有限域GF(23)上時,寫作:
y² ≡ x³ + x + 1 (mod 23)
此時,橢圓曲線不再是一條光滑曲線,而是一些不連續的點,如下圖所示。以點(1,7)為例,7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此還有如下點:
(0,1) (0,22)(1,7) (1,16)(3,10) (3,13)(4,0)(5,4) (5,19)(6,4) (6,19)(7,11) (7,12)(9,7) (9,16)(11,3) (11,20)等等。
另外,如果P(x,y)為橢圓曲線上的點,則-P即(x,-y)也為橢圓曲線上的點。如點P(0,1),-P=(0,-1)=(0,22)也為橢圓曲線上的點。

### 計算xG
相關公式如下:有限域GF(p)上的橢圓曲線y² = x³ + ax + b,若P(Xp, Yp), Q(Xq, Yq),且P≠-Q,則R(Xr,Yr) = P+Q 由如下規則確定:* Xr = (λ² - Xp - Xq) mod p* Yr = (λ(Xp - Xr) - Yp) mod p* 其中λ = (Yq - Yp)/(Xq - Xp) mod p(若P≠Q), λ = (3Xp² + a)/2Yp mod p(若P=Q)
因此,有限域GF(23)上的橢圓曲線y² ≡ x³ + x + 1 (mod 23),假設以(0,1)為G點,計算2G、3G、4G...xG等等,方法如下:
計算2G:* λ = (3x0² + 1)/2x1 mod 23 = (1/2) mod 23 = 12* Xr = (12² - 0 - 0) mod 23 = 6* Yr = (12(0 - 6) - 1) mod 23 = 19即2G為點(6,19)
計算3G:3G = G + 2G,即(0,1) + (6,19)* λ = (19 - 1)/(6 - 0) mod 23 = 3* Xr = (3² - 0 - 6) mod 23 = 3* Yr = (3(0 - 3) - 1) mod 23 = 13即3G為點(3, 13)
同理計算4G、5G...xG,分佈如下圖:

### 橢圓曲線加解密演算法原理
建立基於橢圓曲線的加密機制,需要找到類似RSA質因子分解或其他求離散對數這樣的難題。而橢圓曲線上的已知G和xG求x,是非常困難的,此即為橢圓曲線上的的離散對數問題。此處x即為私鑰,xG即為公鑰。
橢圓曲線加密演算法原理如下:
設私鑰、公鑰分別為k、K,即K = kG,其中G為G點。
公鑰加密:選擇隨機數r,將訊息M生成密文C,該密文是一個點對,即:C = {rG, M+rK},其中K為公鑰
私鑰解密:M + rK - k(rG) = M + r(kG) - k(rG) = M其中k、K分別為私鑰、公鑰。
### 橢圓曲線簽名演算法原理
橢圓曲線簽名演算法,即ECDSA。
設私鑰、公鑰分別為k、K,即K = kG,其中G為G點。
私鑰簽名:* 1、選擇隨機數r,計算點rG(x, y)。* 2、根據隨機數r、訊息M的雜湊h、私鑰k,計算s = (h + kx)/r。* 3、將訊息M、和簽名{rG, s}發給接收方。
公鑰驗證簽名:* 1、接收方收到訊息M、以及簽名{rG=(x,y), s}。* 2、根據訊息求雜湊h。* 3、使用傳送方公鑰K計算:hG/s + xK/s,並與rG比較,如相等即驗籤成功。
原理如下:hG/s + xK/s = hG/s + x(kG)/s = (h+xk)G/s= r(h+xk)G / (h+kx) = rG
### Go語言中橢圓曲線的實現
橢圓曲線的介面定義:
```gotype Curve interface { //獲取橢圓曲線引數 Params() *CurveParams //是否在曲線上 IsOnCurve(x, y *big.Int) bool //加法 Add(x1, y1, x2, y2 *big.Int) (x, y *big.Int) //二倍運算 Double(x1, y1 *big.Int) (x, y *big.Int) //k*(Bx,By) ScalarMult(x1, y1 *big.Int, k []byte) (x, y *big.Int) //k*G, G為基點 ScalarBaseMult(k []byte) (x, y *big.Int)}//程式碼位置src/crypto/elliptic/elliptic.go```
橢圓曲線的介面實現:
```gotype CurveParams struct { //有限域GF(p)中質數p P *big.Int //G點的階 //如果存在最小正整數n,使得nG=O∞,則n為G點的階 N *big.Int //橢圓曲線方程y²= x³-3x+b中常數b B *big.Int //G點(x,y) Gx, Gy *big.Int //金鑰長度 BitSize int //橢圓曲線名稱 Name string}
func (curve *CurveParams) Params() *CurveParams { //獲取橢圓曲線引數,即curve,程式碼略}
func (curve *CurveParams) IsOnCurve(x, y *big.Int) bool { //是否在曲線y²=x³-3x+b上,程式碼略}
func (curve *CurveParams) Add(x1, y1, x2, y2 *big.Int) (*big.Int, *big.Int) { //加法運算,程式碼略}
func (curve *CurveParams) Double(x1, y1 *big.Int) (*big.Int, *big.Int) { //二倍運算,程式碼略}
func (curve *CurveParams) ScalarMult(Bx, By *big.Int, k []byte) (*big.Int, *big.Int) { //k*(Bx,By),程式碼略}
func (curve *CurveParams) ScalarBaseMult(k []byte) (*big.Int, *big.Int) { //k*G, G為基點,程式碼略}//程式碼位置src/crypto/elliptic/elliptic.go```
### Go語言中橢圓曲線簽名的實現
Go標準庫中實現的橢圓曲線簽名原理,與上述理論中基本接近。相關證明方法已註釋在程式碼中。
```go//公鑰type PublicKey struct { elliptic.Curve X, Y *big.Int}
//私鑰type PrivateKey struct { PublicKey //嵌入公鑰 D *big.Int //私鑰}
func Sign(rand io.Reader, priv *PrivateKey, hash []byte) (r, s *big.Int, err error) { entropylen := (priv.Curve.Params().BitSize + 7) / 16 if entropylen > 32 { entropylen = 32 } entropy := make([]byte, entropylen) _, err = io.ReadFull(rand, entropy) if err != nil { return }
md := sha512.New() md.Write(priv.D.Bytes()) //私鑰 md.Write(entropy) md.Write(hash) key := md.Sum(nil)[:32]
block, err := aes.NewCipher(key) if err != nil { return nil, nil, err }
csprng := cipher.StreamReader{ R: zeroReader, S: cipher.NewCTR(block, []byte(aesIV)), }
c := priv.PublicKey.Curve //橢圓曲線 N := c.Params().N //G點的階 if N.Sign() == 0 { return nil, nil, errZeroParam } var k, kInv *big.Int for { for { //取隨機數k k, err = randFieldElement(c, csprng) if err != nil { r = nil return }
//求k在有限域GF(P)的逆,即1/k if in, ok := priv.Curve.(invertible); ok { kInv = in.Inverse(k) } else { kInv = fermatInverse(k, N) // N != 0 }
//求r = kG r, _ = priv.Curve.ScalarBaseMult(k.Bytes()) r.Mod(r, N) if r.Sign() != 0 { break } }
e := hashToInt(hash, c) //e即雜湊 s = new(big.Int).Mul(priv.D, r) //Dr,即DkG s.Add(s, e) //e+DkG s.Mul(s, kInv) //(e+DkG)/k s.Mod(s, N) // N != 0 if s.Sign() != 0 { break } //簽名為{r, s},即{kG, (e+DkG)/k} }
return}
//驗證簽名func Verify(pub *PublicKey, hash []byte, r, s *big.Int) bool { c := pub.Curve //橢圓曲線 N := c.Params().N //G點的階
if r.Sign() <= 0 || s.Sign() <= 0 { return false } if r.Cmp(N) >= 0 || s.Cmp(N) >= 0 { return false } e := hashToInt(hash, c) //e即雜湊
var w *big.Int //求s在有限域GF(P)的逆,即1/s if in, ok := c.(invertible); ok { w = in.Inverse(s) } else { w = new(big.Int).ModInverse(s, N) }
u1 := e.Mul(e, w) //即e/s u1.Mod(u1, N) u2 := w.Mul(r, w) //即r/s u2.Mod(u2, N)
var x, y *big.Int if opt, ok := c.(combinedMult); ok { x, y = opt.CombinedMult(pub.X, pub.Y, u1.Bytes(), u2.Bytes()) } else { x1, y1 := c.ScalarBaseMult(u1.Bytes()) //即eG/s x2, y2 := c.ScalarMult(pub.X, pub.Y, u2.Bytes()) //即DGr/s //即eG/s + DGr/s = (e + Dr)G/s //= (e + Dr)kG / (e + DkG) = (e + Dr)r / (e + Dr) = r x, y = c.Add(x1, y1, x2, y2) }
if x.Sign() == 0 && y.Sign() == 0 { return false } x.Mod(x, N) return x.Cmp(r) == 0}//程式碼位置src/crypto/ecdsa/ecdsa.go```
### 後記
橢圓曲線數字簽名演算法,因其高安全性,目前已廣泛應用在比特幣、以太坊、超級賬本等區塊鏈專案中。
橢圓曲線加密演算法,即:Elliptic Curve Cryptography,簡稱ECC,是基於橢圓曲線數學理論實現的一種非對稱加密演算法。相比RSA,ECC優勢是可以使用更短的金鑰,來實現與RSA相當或更高的安全。據研究,160位ECC加密安全性相當於1024位RSA加密,210位ECC加密安全性相當於2048位RSA加密。
橢圓曲線在密碼學中的使用,是1985年由Neal Koblitz和Victor Miller分別獨立提出的。
### 橢圓曲線
一般,橢圓曲線可以用如下二元三階方程表示:y² = x³ + ax + b,其中a、b為係數。
如果滿足條件4a³+27b²≠0,則可以基於E(a, b)定義一個群。
其形狀如下:

### 定義橢圓曲線的運算規則
橢圓曲線上的運算規則,由如下方式定義:
加法:過曲線上的兩點A、B畫一條直線,找到直線與橢圓曲線的交點,交點關於x軸對稱位置的點,定義為A+B,即為加法。如下圖所示:
A + B = C

二倍運算:上述方法無法解釋A + A,即兩點重合的情況。因此在這種情況下,將橢圓曲線在A點的切線,與橢圓曲線的交點,交點關於x軸對稱位置的點,定義為A + A,即2A,即為二倍運算。如下圖所示:
A + A = 2A = B

正負取反:將A關於x軸對稱位置的點定義為-A,即橢圓曲線的正負取反運算。如下圖所示:

無窮遠點:如果將A與-A相加,過A與-A的直線平行於y軸,可以認為直線與橢圓曲線相交於無窮遠點。如下圖所示:

綜上,定義了A+B、2A運算,因此給定橢圓曲線的某一點G,可以求出2G、3G(即G + 2G)、4G......。即:當給定G點時,已知x,求xG點並不困難。反之,已知xG點,求x則非常困難。此即為橢圓曲線加密演算法背後的數學原理。
### 有限域上的橢圓曲線運算
橢圓曲線要形成一條光滑的曲線,要求x,y取值均為實數,即實數域上的橢圓曲線。但橢圓曲線加密演算法,並非使用實數域,而是使用有限域。按數論定義,有限域GF(p)指給定某個質數p,由0、1、2......p-1共p個元素組成的整數集合中定義的加減乘除運算。
假設橢圓曲線為y² = x³ + x + 1,其在有限域GF(23)上時,寫作:
y² ≡ x³ + x + 1 (mod 23)
此時,橢圓曲線不再是一條光滑曲線,而是一些不連續的點,如下圖所示。以點(1,7)為例,7² ≡ 1³ + 1 + 1 ≡ 3 (mod 23)。如此還有如下點:
(0,1) (0,22)(1,7) (1,16)(3,10) (3,13)(4,0)(5,4) (5,19)(6,4) (6,19)(7,11) (7,12)(9,7) (9,16)(11,3) (11,20)等等。
另外,如果P(x,y)為橢圓曲線上的點,則-P即(x,-y)也為橢圓曲線上的點。如點P(0,1),-P=(0,-1)=(0,22)也為橢圓曲線上的點。

### 計算xG
相關公式如下:有限域GF(p)上的橢圓曲線y² = x³ + ax + b,若P(Xp, Yp), Q(Xq, Yq),且P≠-Q,則R(Xr,Yr) = P+Q 由如下規則確定:* Xr = (λ² - Xp - Xq) mod p* Yr = (λ(Xp - Xr) - Yp) mod p* 其中λ = (Yq - Yp)/(Xq - Xp) mod p(若P≠Q), λ = (3Xp² + a)/2Yp mod p(若P=Q)
因此,有限域GF(23)上的橢圓曲線y² ≡ x³ + x + 1 (mod 23),假設以(0,1)為G點,計算2G、3G、4G...xG等等,方法如下:
計算2G:* λ = (3x0² + 1)/2x1 mod 23 = (1/2) mod 23 = 12* Xr = (12² - 0 - 0) mod 23 = 6* Yr = (12(0 - 6) - 1) mod 23 = 19即2G為點(6,19)
計算3G:3G = G + 2G,即(0,1) + (6,19)* λ = (19 - 1)/(6 - 0) mod 23 = 3* Xr = (3² - 0 - 6) mod 23 = 3* Yr = (3(0 - 3) - 1) mod 23 = 13即3G為點(3, 13)
同理計算4G、5G...xG,分佈如下圖:

### 橢圓曲線加解密演算法原理
建立基於橢圓曲線的加密機制,需要找到類似RSA質因子分解或其他求離散對數這樣的難題。而橢圓曲線上的已知G和xG求x,是非常困難的,此即為橢圓曲線上的的離散對數問題。此處x即為私鑰,xG即為公鑰。
橢圓曲線加密演算法原理如下:
設私鑰、公鑰分別為k、K,即K = kG,其中G為G點。
公鑰加密:選擇隨機數r,將訊息M生成密文C,該密文是一個點對,即:C = {rG, M+rK},其中K為公鑰
私鑰解密:M + rK - k(rG) = M + r(kG) - k(rG) = M其中k、K分別為私鑰、公鑰。
### 橢圓曲線簽名演算法原理
橢圓曲線簽名演算法,即ECDSA。
設私鑰、公鑰分別為k、K,即K = kG,其中G為G點。
私鑰簽名:* 1、選擇隨機數r,計算點rG(x, y)。* 2、根據隨機數r、訊息M的雜湊h、私鑰k,計算s = (h + kx)/r。* 3、將訊息M、和簽名{rG, s}發給接收方。
公鑰驗證簽名:* 1、接收方收到訊息M、以及簽名{rG=(x,y), s}。* 2、根據訊息求雜湊h。* 3、使用傳送方公鑰K計算:hG/s + xK/s,並與rG比較,如相等即驗籤成功。
原理如下:hG/s + xK/s = hG/s + x(kG)/s = (h+xk)G/s= r(h+xk)G / (h+kx) = rG
### Go語言中橢圓曲線的實現
橢圓曲線的介面定義:
```gotype Curve interface { //獲取橢圓曲線引數 Params() *CurveParams //是否在曲線上 IsOnCurve(x, y *big.Int) bool //加法 Add(x1, y1, x2, y2 *big.Int) (x, y *big.Int) //二倍運算 Double(x1, y1 *big.Int) (x, y *big.Int) //k*(Bx,By) ScalarMult(x1, y1 *big.Int, k []byte) (x, y *big.Int) //k*G, G為基點 ScalarBaseMult(k []byte) (x, y *big.Int)}//程式碼位置src/crypto/elliptic/elliptic.go```
橢圓曲線的介面實現:
```gotype CurveParams struct { //有限域GF(p)中質數p P *big.Int //G點的階 //如果存在最小正整數n,使得nG=O∞,則n為G點的階 N *big.Int //橢圓曲線方程y²= x³-3x+b中常數b B *big.Int //G點(x,y) Gx, Gy *big.Int //金鑰長度 BitSize int //橢圓曲線名稱 Name string}
func (curve *CurveParams) Params() *CurveParams { //獲取橢圓曲線引數,即curve,程式碼略}
func (curve *CurveParams) IsOnCurve(x, y *big.Int) bool { //是否在曲線y²=x³-3x+b上,程式碼略}
func (curve *CurveParams) Add(x1, y1, x2, y2 *big.Int) (*big.Int, *big.Int) { //加法運算,程式碼略}
func (curve *CurveParams) Double(x1, y1 *big.Int) (*big.Int, *big.Int) { //二倍運算,程式碼略}
func (curve *CurveParams) ScalarMult(Bx, By *big.Int, k []byte) (*big.Int, *big.Int) { //k*(Bx,By),程式碼略}
func (curve *CurveParams) ScalarBaseMult(k []byte) (*big.Int, *big.Int) { //k*G, G為基點,程式碼略}//程式碼位置src/crypto/elliptic/elliptic.go```
### Go語言中橢圓曲線簽名的實現
Go標準庫中實現的橢圓曲線簽名原理,與上述理論中基本接近。相關證明方法已註釋在程式碼中。
```go//公鑰type PublicKey struct { elliptic.Curve X, Y *big.Int}
//私鑰type PrivateKey struct { PublicKey //嵌入公鑰 D *big.Int //私鑰}
func Sign(rand io.Reader, priv *PrivateKey, hash []byte) (r, s *big.Int, err error) { entropylen := (priv.Curve.Params().BitSize + 7) / 16 if entropylen > 32 { entropylen = 32 } entropy := make([]byte, entropylen) _, err = io.ReadFull(rand, entropy) if err != nil { return }
md := sha512.New() md.Write(priv.D.Bytes()) //私鑰 md.Write(entropy) md.Write(hash) key := md.Sum(nil)[:32]
block, err := aes.NewCipher(key) if err != nil { return nil, nil, err }
csprng := cipher.StreamReader{ R: zeroReader, S: cipher.NewCTR(block, []byte(aesIV)), }
c := priv.PublicKey.Curve //橢圓曲線 N := c.Params().N //G點的階 if N.Sign() == 0 { return nil, nil, errZeroParam } var k, kInv *big.Int for { for { //取隨機數k k, err = randFieldElement(c, csprng) if err != nil { r = nil return }
//求k在有限域GF(P)的逆,即1/k if in, ok := priv.Curve.(invertible); ok { kInv = in.Inverse(k) } else { kInv = fermatInverse(k, N) // N != 0 }
//求r = kG r, _ = priv.Curve.ScalarBaseMult(k.Bytes()) r.Mod(r, N) if r.Sign() != 0 { break } }
e := hashToInt(hash, c) //e即雜湊 s = new(big.Int).Mul(priv.D, r) //Dr,即DkG s.Add(s, e) //e+DkG s.Mul(s, kInv) //(e+DkG)/k s.Mod(s, N) // N != 0 if s.Sign() != 0 { break } //簽名為{r, s},即{kG, (e+DkG)/k} }
return}
//驗證簽名func Verify(pub *PublicKey, hash []byte, r, s *big.Int) bool { c := pub.Curve //橢圓曲線 N := c.Params().N //G點的階
if r.Sign() <= 0 || s.Sign() <= 0 { return false } if r.Cmp(N) >= 0 || s.Cmp(N) >= 0 { return false } e := hashToInt(hash, c) //e即雜湊
var w *big.Int //求s在有限域GF(P)的逆,即1/s if in, ok := c.(invertible); ok { w = in.Inverse(s) } else { w = new(big.Int).ModInverse(s, N) }
u1 := e.Mul(e, w) //即e/s u1.Mod(u1, N) u2 := w.Mul(r, w) //即r/s u2.Mod(u2, N)
var x, y *big.Int if opt, ok := c.(combinedMult); ok { x, y = opt.CombinedMult(pub.X, pub.Y, u1.Bytes(), u2.Bytes()) } else { x1, y1 := c.ScalarBaseMult(u1.Bytes()) //即eG/s x2, y2 := c.ScalarMult(pub.X, pub.Y, u2.Bytes()) //即DGr/s //即eG/s + DGr/s = (e + Dr)G/s //= (e + Dr)kG / (e + DkG) = (e + Dr)r / (e + Dr) = r x, y = c.Add(x1, y1, x2, y2) }
if x.Sign() == 0 && y.Sign() == 0 { return false } x.Mod(x, N) return x.Cmp(r) == 0}//程式碼位置src/crypto/ecdsa/ecdsa.go```
### 後記
橢圓曲線數字簽名演算法,因其高安全性,目前已廣泛應用在比特幣、以太坊、超級賬本等區塊鏈專案中。
網址:http://www.qukuailianxueyuan.io/
欲領取造幣技術與全套虛擬機器資料
區塊鏈技術交流QQ群:756146052 備註:CSDN
尹成學院微信:備註:CSDN