0.綜述

     給出房價與房屋面積的關係，利用梯度下降的方法進行資料擬合，並對給定的房屋面積做出對房價的預測。

1.warmUpExercise

      輸出5*5的單位矩陣

function A = warmUpExercise()
%WARMUPEXERCISE Example function in octave
%   A = WARMUPEXERCISE() is an example function that returns the 5x5 identity matrix

A = [];
% ============= YOUR CODE HERE ==============
% Instructions: Return the 5x5 identity matrix 
%               In octave, we return values by defining which variables
%               represent the return values (at the top of the file)
%               and then set them accordingly. 


A = eye(5);    %輸出單位矩陣




% ===========================================


end
 

2.plotData

      要求把資料繪製成影象

      這是指令碼中的呼叫plotData函式的程式碼

%% ======================= Part 2: Plotting =======================
fprintf('Plotting Data ...\n')
data = load('ex1data1.txt');         %開啟資料
X = data(:, 1); y = data(:, 2);      %x軸是第一列資料，y軸式第二列資料
m = length(y); % number of training examples

% Plot Data
% Note: You have to complete the code in plotData.m
plotData(X, y);

fprintf('Program paused. Press enter to continue.\n');
pause;

 

      這是畫圖的程式碼

function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure 
%   PLOTDATA(x,y) plots the data points and gives the figure axes labels of
%   population and profit.

% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the 
%               "figure" and "plot" commands. Set the axes labels using
%               the "xlabel" and "ylabel" commands. Assume the 
%               population and revenue data have been passed in
%               as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
%       appear as red crosses. Furthermore, you can make the
%       markers larger by using plot(..., 'rx', 'MarkerSize', 10);

figure; % open a new figure window
plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data
ylabel('Profit in $10,000s'); % Set the y   axis label
xlabel('Population of City in 10,000s'); % Set the x   axis label

 

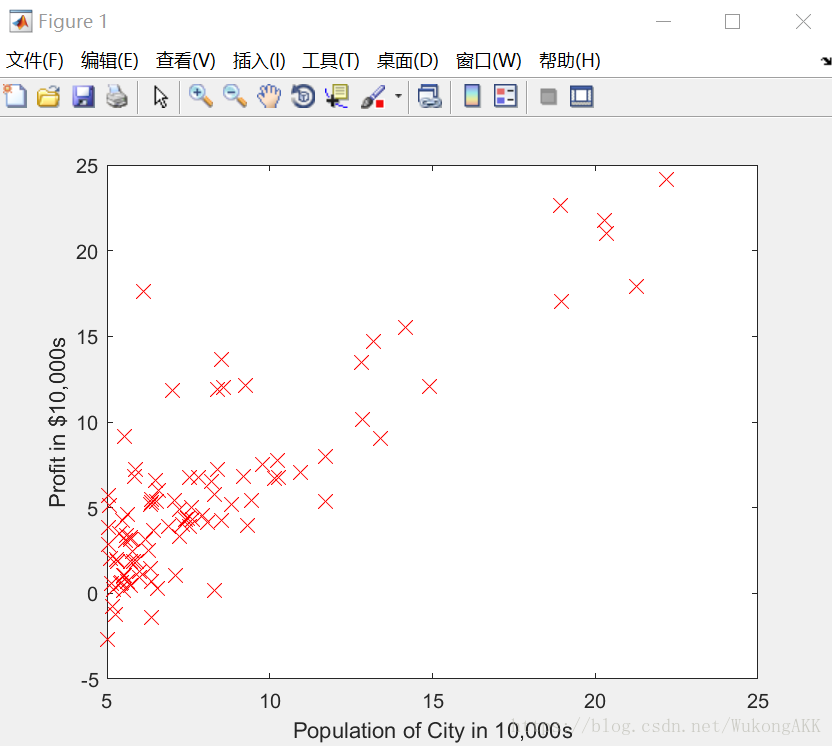
    這是畫好的影象

.

3.Gradient descent

    這一部分是關於梯度下降的，先看指令碼中的程式碼

%% =================== Part 3: Gradient descent ===================
fprintf('Running Gradient Descent ...\n')

X = [ones(m, 1), data(:,1)]; % Add a column of ones to x 這是加了一行1，使資料可以進行矩陣運算
theta = zeros(2, 1); % initialize fitting parameters  初始化theta為0

% Some gradient descent settings
iterations = 1500;                 %迭代次數設為1500，進化速率為0.01
alpha = 0.01;

% compute and display initial cost
computeCost(X, y, theta)

% run gradient descent
theta = gradientDescent(X, y, theta, alpha, iterations);       %梯度下降求出theta矩陣

% print theta to screen
fprintf('Theta found by gradient descent: ');
fprintf('%f %f \n', theta(1), theta(2));

% Plot the linear fit
hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')                                     %畫出擬合後的線性影象
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure

% Predict values for population sizes of 35,000 and 70,000
predict1 = [1, 3.5] *theta;
fprintf('For population = 35,000, we predict a profit of %f\n',...
    predict1*10000);
predict2 = [1, 7] * theta;
fprintf('For population = 70,000, we predict a profit of %f\n',...
    predict2*10000);

fprintf('Program paused. Press enter to continue.\n');
pause;

    計算誤差的程式碼

function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
%   J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
%   parameter for linear regression to fit the data points in X and y

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
%               You should set J to the cost.
J = sum((X * theta - y).^2) / (2*m);     % X(79,2)  theta(2,1)
% X為資料矩陣，用X*thera-y算出誤差，求平方後用sum函式求和再除以2*m,得到J。
% 其中.^2是對矩陣中的每個元素求平方



% =========================================================================

end

    梯度下降的程式碼

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
%   theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by 
%   taking num_iters gradient steps with learning rate alpha

% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_s=theta;

for iter = 1:num_iters

    % ====================== YOUR CODE HERE ======================
    % Instructions: Perform a single gradient step on the parameter vector
    %               theta. 
    %
    % Hint: While debugging, it can be useful to print out the values
    %       of the cost function (computeCost) and gradient here.
    %
    theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);       
    theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));     % 必須同時更新theta(1)和theta(2)，所以不能用X * theta,而要用theta_s儲存上次結果。
    theta_s=theta; 
    

    % ============================================================

    % Save the cost J in every iteration    
    J_history(iter) = computeCost(X, y, theta);

end
J_history                                         %輸出整個J矩陣
end

4.Visualizing J

    這部分就是畫出梯度下降的影象，使我們對梯度下降尋找合適的theta有一個更加直觀的感受。

    先看指令碼

%% ============= Part 4: Visualizing J(theta_0, theta_1) =============
fprintf('Visualizing J(theta_0, theta_1) ...\n')

% Grid over which we will calculate J
theta0_vals = linspace(-10, 10, 100);    % theta0_vals為-10到10的100個數，且是一個行向量
theta1_vals = linspace(-1, 4, 100);

% initialize J_vals to a matrix of 0's
J_vals = zeros(length(theta0_vals), length(theta1_vals));      %構造n*n的0矩陣

% Fill out J_vals
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
	  t = [theta0_vals(i); theta1_vals(j)];                   %“；”是在構造列向量
	  J_vals(i,j) = computeCost(X, y, t);
    end
end


% Because of the way meshgrids work in the surf command, we need to 
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals';
% Surface plot
figure;                                                      %建立一個視窗
surf(theta0_vals, theta1_vals, J_vals)                       %畫圖，J由theta0和theta1確定
xlabel('\theta_0'); ylabel('\theta_1');

% Contour plot                                               %輪廓圖
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))         %畫20條等高線，每條等高線的值根據theta0,theta1,J,在10^(-2)和10^3依次對應一個值
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

    這是最後兩幅圖的效果