人工智慧: 自動尋路演算法實現(三、A*演算法)
本篇文章是機器人自動尋路演算法實現的第三章。我們要討論的是一個在一個M×N的格子的房間中,有若干格子裡有灰塵,有若干格子裡有障礙物,而我們的掃地機器人則是要在不經過障礙物格子的前提下清理掉房間內的灰塵。具體的問題情景請檢視人工智慧: 自動尋路演算法實現(一、廣度優先搜尋)這篇文章,即我們這個系列的第一篇文章。在前兩篇文章裡,我們介紹了通過廣度優先搜尋演算法和深度優先演算法來實現掃地機器人自動尋路的功能。兩種演算法都有各自的優點和缺點:對於廣度優先搜尋演算法,程式會找到最優解,但是需要遍歷的節點很多。而深度優先搜尋則與之相反:遍歷的節點很少,但是不一定會找到最優解,而且還有一種極端的情況,就是深度優先搜尋在遍歷的時候,如果遍歷的那個分支是無限大,並且解並不在那個分支中而是在其他的分支中,那麼深度優先搜尋永遠都找不到解。兩種演算法具體的比較在
A*演算法被廣泛應用於遊戲中的自動尋路功能,說明它作為一個路徑規劃的演算法,確實有著很大的優勢。以遊戲舉例來看,比如在遊戲中我們想要找到從一個位置到另一個位置的路徑,我們不僅嘗試著找到最短距離的路徑;我們還想要顧忌到消耗的時間。在一張地圖上,穿過一片池塘速度會明顯減慢,所以我們想要找到一條可以繞過水路的路徑。
正文
演算法介紹
首先我們來回顧一下廣度優先搜尋和深度優先搜尋演算法。我們從前兩篇文章中可以得知,廣度優先搜尋演算法中使用資料結構是佇列,而深度優先搜尋演算法中適用的資料結構是棧。對於一個佇列,節點總是先進先出(FIFO),因此對於佇列中的第一個節點
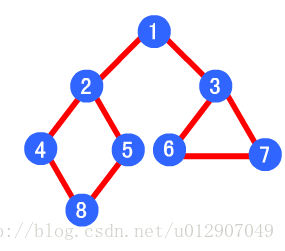
廣度優先搜尋的節點遍歷順序
而相對地,深度優先搜尋就很好理解。對於任何一個節點,都會先去遍歷它的第一個子節點的第一個子節點的第一個子節點…後進先出(LIFO)的棧則正好保證了這一點。這種“一條路走到黑
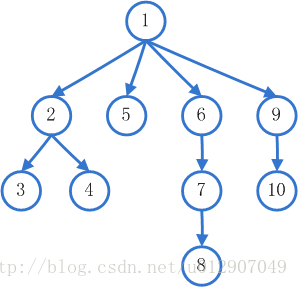
深度優先搜尋的節點遍歷順序
這兩種演算法的優缺點都很明顯,於是我們需要想出一種能結合兩種演算法優點的演算法。我們可以做出如下處理:對於廣度優先搜尋演算法的佇列,如果我們可以想出一種方法,對佇列進行排序,把前文中類似“穿過一片沼澤”這樣的節點儘量放在最後去遍歷,那麼我們就可以在相對短的時間內找出一個最優解來。在A*演算法中,我們對節點按以下的方式進行排序:
F = G + H- 1
其中,F是我們計算出的權值,F值越大,代表這個節點的收益越小,也就越接近於我們上文提到的“沼澤地”。
G指的是我們從初始節點到達現在的節點的過程中付出的代價。例如我們的機器人每走一格或每清理一個灰塵會耗費1個單位時間,那麼機器人做了5個動作之後,我們的G值就是5。
H值是一個相對開放的概念,它指的是從目前狀態到目標狀態預計要付出的代價。這個值由演算法工程師來進行估算,H值被估算的越準確,演算法所需要遍歷的節點就越少。以我們的掃地機器人舉例,假如目前房間內只剩下一個灰塵,而這個灰塵就在機器人的東側(右側),那麼機器人通過這種演算法就可以直接選擇先往東走去清理這個灰塵,而不是向其他方向走,避免了“南轅北轍”這種人工智障???的情況出現。

計算出這個值之後,我們就按這個F值在佇列中進行排序。本例中原始碼由Java編寫,在Java中有一種資料結構,PriorityQueue,即優先順序佇列,這種資料結構正好可以用來存放要遍歷的節點。
程式碼
首先是Point類,用於表示座標系中的點。這個檔案與前兩個演算法中相同。程式碼如下:
public class Point {
private int X;
private int Y;
public Point(int x, int y){
this.X = x;
this.Y = y;
}
public int getX() {
return X;
}
public void setX(int x) {
X = x;
}
public int getY() {
return Y;
}
public void setY(int y) {
Y = y;
}
//判斷兩個點是否座標相同
public static boolean isSamePoint(Point point1, Point point2){
if(point1.getX() == point2.getX() && point1.getY() == point2.getY())
return true;
return false;
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
接下來是State類。如果把問題的情景(房間、機器人)比作一個系統,那麼State類就表示某一時刻系統的狀態,也就是我們要遍歷的節點。注意這個類裡比之前的兩個演算法多了兩個屬性,F值和G值。G值就是機器人從其實狀態到當前狀態所進行的操作次數。F值是G值和H值的和。而H值,在這裡並沒有列出來,因為我把它視為當前狀態下仍未被清理的灰塵數量,也就是灰塵列表的size,通過當前狀態的dirtList取size()即可得到,便不再單獨設該屬性。
import java.util.ArrayList;
import java.util.List;
public class State {
//機器人位置
private Point robotLocation;
//操作,分為N(向上移動一格), S(向下移動一格), W(向左移動一格), E(向右移動一格)以及C(清理灰塵)
private String operation;
//當前節點的父節點, 用於達到目標後進行回溯
private State previousState;
//灰塵所在座標的list
private List<Point> dirtList;
//fvalue為gvalue和hvalue的和
private int fvalue;
//gvalue
private int cost;
public Point getRobotLocation() {
return robotLocation;
}
public void setRobotLocation(Point robotLocation) {
this.robotLocation = robotLocation;
}
public String getOperation() {
return operation;
}
public void setOperation(String operation) {
this.operation = operation;
}
public State getPreviousState() {
return previousState;
}
public void setPreviousState(State previousState) {
this.previousState = previousState;
}
public List<Point> getDirtList() {
return dirtList;
}
public void setDirtList(List<Point> dirtList) {
this.dirtList = new ArrayList<Point>();
for(Point point : dirtList){
this.dirtList.add(point);
}
}
public int getFvalue() {
return fvalue;
}
public void setFvalue(int fvalue) {
this.fvalue = fvalue;
}
public int getCost() {
return cost;
}
public void setCost(int cost) {
this.cost = cost;
}
//用於判斷兩個節點是否相同
public static boolean isSameState(State state1, State state2){
//若機器人位置不同,則節點不同
if(!Point.isSamePoint(state1.getRobotLocation(), state2.getRobotLocation()))
return false;
//若灰塵列表長度不同, 則節點不同
else if(state1.getDirtList().size() != state2.getDirtList().size())
return false;
//若前兩者都相同, 則判斷兩個state中的灰塵列表中的灰塵座標是否完全相同
else{
for(Point point : state1.getDirtList())
{
boolean same = false;
for(Point point2 : state2.getDirtList())
{
if(Point.isSamePoint(point, point2))
same = true;
}
if(!same)
return false;
}
}
//若滿足上述所有條件, 則兩節點相同。
return true;
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
最後是演算法的實現類,Robot類。該類使用了一個新的資料結構:PriorityQueue來作為儲存節點的open list。PriorityQueue需要我們自定義一個比較器(Comparator)用於在插入元素時將該元素與列表中的元素進行比較,並插入適當的位置,保證PriorityQueue在任何時刻都是有序的。需要注意的一點是我們需要把F值較小的元素排在前面。
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class Robot {
//行數
public static int colomnNum;
//列數
public static int rowNum;
//障礙物數量
public static int obstacleNum;
//用於存放state的優先順序佇列
public static Queue<State> priorityQueue;
//地圖
public static String[][] map;
//灰塵座標列表
public static List<Point> dirtList;
//closeList,用於存放已經存在的state
public static List<State> closeList;
//遍歷總耗費
public static int cost = 0;
public static void main(String[] args) {
State initialState = new State();
Scanner sc = new Scanner(System.in);
System.out.println("Please Enter Row Number:");
rowNum = sc.nextInt();
System.out.println("Please Enter Colomn Number:");
colomnNum = sc.nextInt();
map = new String[rowNum][colomnNum];
dirtList = new ArrayList<Point>();
closeList = new ArrayList<State>();
sc.nextLine();
for(int i=0; i<rowNum; i++)
{
System.out.println("Please Enter the Elements in row " + (i + 1) + ":");
String line = sc.nextLine();
for(int j=0; j<colomnNum; j++)
{
//統計障礙物數量
if(line.charAt(j) == '#')
{
obstacleNum++;
}
//將灰塵格子座標存入list中
if(line.charAt(j) == '*')
{
dirtList.add(new Point(i, j));
}
//設定機器人初始座標
if(line.charAt(j) == '@')
{
initialState.setRobotLocation(new Point(i, j));
}
//初始化地圖
map[i][j] = line.charAt(j) + "";
}
}
sc.close();
initialState.setDirtList(dirtList);
initialState.setCost(0);
initialState.setFvalue(0 + dirtList.size());
//優先順序佇列的自定義Comparator,比較規則是Fvalue較小的state排在佇列前面
Comparator<State> cmp = new Comparator<State>() {
public int compare(State s1, State s2) {
return s1.getFvalue() - s2.getFvalue();
}
};
//初始化優先順序佇列
priorityQueue = new PriorityQueue<State>(5, cmp);
closeList.add(initialState);
priorityQueue.add(initialState);
cost++;
//遍歷開始
while(!priorityQueue.isEmpty()){
//取出佇列中第一個state
State state = priorityQueue.poll();
//如果達到目標,輸出結果並退出
if(isgoal(state)){
output(state);
return;
}
calculate(state);
}
}
public static void calculate(State state){
//獲取當前機器人的座標
int x = state.getRobotLocation().getX();
int y = state.getRobotLocation().getY();
//如果當前的點是灰塵並且沒有被清理
if(map[x][y].equals("*") && !isCleared(new Point(x, y), state.getDirtList())){
State newState = new State();
List<Point> newdirtList = new ArrayList<Point>();
//在新的state中,將灰塵列表更新,即去掉當前點的座標
for(Point point : state.getDirtList())
{
if(point.getX() == x && point.getY() == y)
continue;
else
newdirtList.add(new Point(point.getX(), point.getY()));
}
newState.setDirtList(newdirtList);
newState.setCost(state.getCost() + 1);
//Fvalue為gvalue和hvalue的和
newState.setFvalue(newState.getCost() + newdirtList.size());
newState.setRobotLocation(new Point(x, y));
//C代表Clean操作
newState.setOperation("C");
newState.setPreviousState(state);
//若新產生的狀態與任意一個遍歷過的狀態都不同,則進入佇列
if(!isDuplicated(newState)){
priorityQueue.add(newState);
closeList.add(newState);
cost++;
}
}
//若當前機器人座標下方有格子並且不是障礙物
if(x + 1 < rowNum)
{
if(!map[x+1][y].equals("#"))
{
State newState = new State();
newState.setDirtList(state.getDirtList());
newState.setRobotLocation(new Point(x + 1, y));
//S代表South,即向下方移動一個格子
newState.setOperation("S");
newState.setCost(state.getCost() + 1);
newState.setFvalue(newState.getCost() + state.getDirtList().size());
newState.setPreviousState(state);
if(!isDuplicated(newState)){
priorityQueue.add(newState);
//加入到closeList中
closeList.add(newState);
cost++;
}
}
}
//若當前機器人座標上方有格子並且不是障礙物
if(x - 1 >= 0)
{
if(!map[x-1][y].equals("#"))
{
State newState = new State();
newState.setDirtList(state.getDirtList());
newState.setRobotLocation(new Point(x - 1, y));
//N代表North,即向上方移動一個格子
newState.setOperation("N");
newState.setCost(state.getCost() + 1);
newState.setFvalue(newState.getCost() + state.getDirtList().size());
newState.setPreviousState(state);
if(!isDuplicated(newState)){
priorityQueue.add(newState);
closeList.add(newState);
cost++;
}
}
}
//若當前機器人座標左側有格子並且不是障礙物
if(y - 1 >= 0)
{
if(!map[x][y-1].equals("#"))
{
State newState = new State();
newState.setDirtList(state.getDirtList());
newState.setRobotLocation(new Point(x, y - 1));
//W代表West,即向左側移動一個格子
newState.setOperation("W");
newState.setCost(state.getCost() + 1);
newState.setFvalue(newState.getCost() + state.getDirtList().size());
newState.setPreviousState(state);
if(!isDuplicated(newState)){
priorityQueue.add(newState);
closeList.add(newState);
cost++;
}
}
}
//若當前機器人座標右側有格子並且不是障礙物
if(y + 1 < colomnNum)
{
if(!map[x][y+1].equals("#"))
{
State newState = new State();
newState.setDirtList(state.getDirtList());
newState.setRobotLocation(new Point(x, y + 1));
//E代表East,即向右側移動一個格子
newState.setOperation("E");
newState.setCost(state.getCost() + 1);
newState.setFvalue(newState.getCost() + state.getDirtList().size());
newState.setPreviousState(state);
if(!isDuplicated(newState)){
priorityQueue.add(newState);
closeList.add(newState);
cost++;
}
}
}
}
//判斷是否已經達到目標,即當前遍歷到的state中手否已經沒有灰塵需要清理
public static boolean isgoal(State state){
if(state.getDirtList().isEmpty())
return true;
return false;
}
//輸出,由最後一個state一步一步回溯到起始state
public static void output(State state){
String output = "";
//回溯期間把每一個state的操作(由於直接輸出的話是倒序)加入到output字串之前,再輸出output
while(state != null){
if(state.getOperation() != null)
output = state.getOperation() + "\r\n" + output;
state = state.getPreviousState();
}
System.out.println(output);
//最後輸出遍歷過的節點(state)數量
System.out.println(cost);
}
//判斷節點是否存在,即將state與closeList中的state相比較,若都不相同則為全新節點
public static boolean isDuplicated(State state){
for(State state2 : closeList){
if(State.isSameState(state, state2))
return true;
}
return false;
}
//判斷地圖中當前位置的灰塵在這個state中是否已經被除去。
public static boolean isCleared(Point point, List<Point> list){
for(Point p : list){
if(Point.isSamePoint(p, point))
return false;
}
return true;
}
} - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
- 179
- 180
- 181
- 182
- 183
- 184
- 185
- 186
- 187
- 188
- 189
- 190
- 191
- 192
- 193
- 194
- 195
- 196
- 197
- 198
- 199
- 200
- 201
- 202
- 203
- 204
- 205
- 206
- 207
- 208
- 209
- 210
- 211
- 212
- 213
- 214
- 215
- 216
- 217
- 218
- 219
- 220
- 221 <
