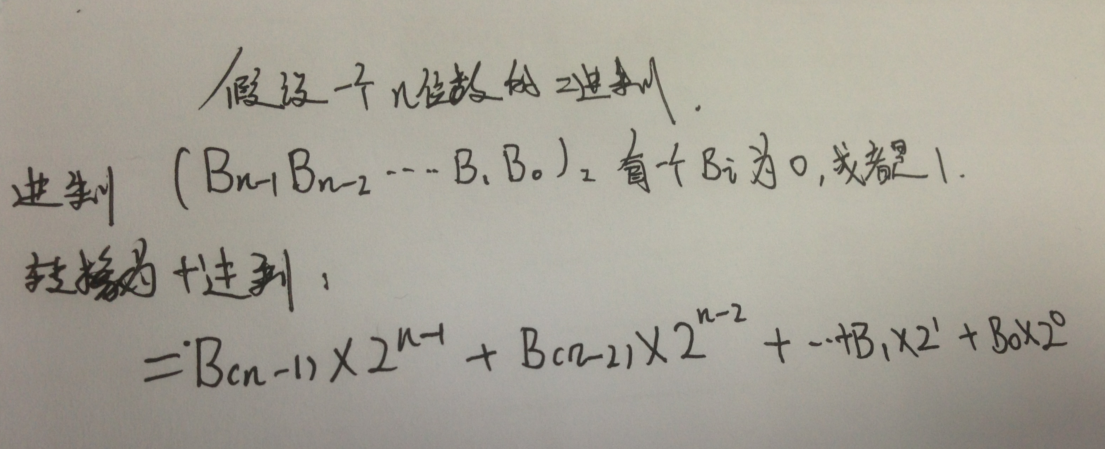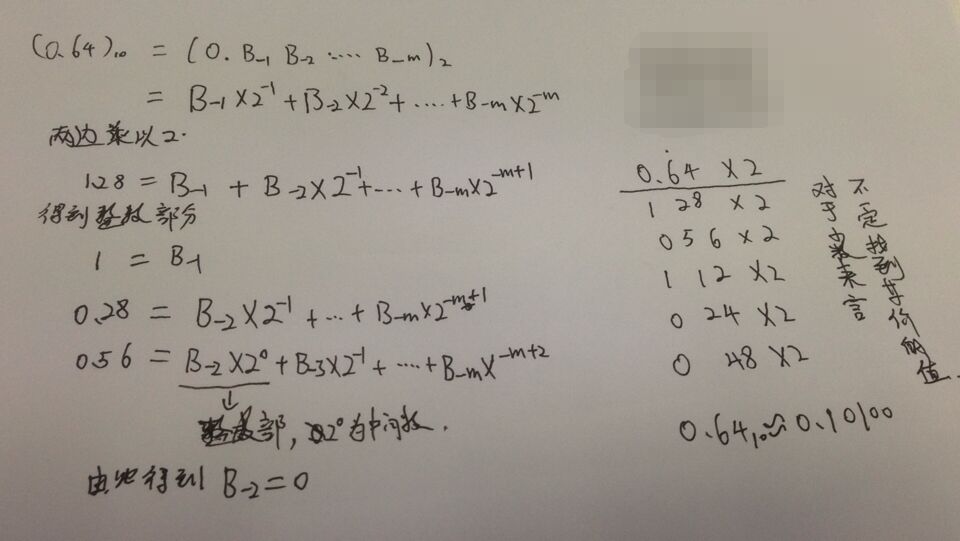十進位制與二進位制相互轉換(包括帶小數點.各類進位制轉換公式)
阿新 • • 發佈:2019-02-08
首先從進位制,來討論
十進位制
0-1-2-3-4-5-6-7-8-9
例如:
365.32(十進位制)
小數點左等於
3*10^2+6*10^1+5*10^0
右邊等於
3*10^-1 + 2*10^-2
綜合結果=
3*10^2+6*10^1+5*10^0+3*10^-1 + 2*10^-2
10在十進位制中叫做10進位制的基數
在十進位制中相鄰的差距是10倍,
(不知道10^-1次方的可以自行看圖)
{
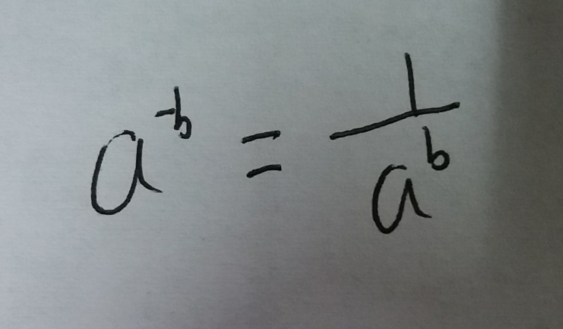
}
二進位制:
2為2進位制的的基數逢2進1
| 十進位制 | 二進位制 |
|---|---|
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
在十進位制中相鄰的差距是10倍,在二進位制中是二倍
110 這個數展開得到
1*2^2+1*2^1+0*2^0=
轉為10進位制等於=6
帶小數點的
110.11=
1*2^2+1*2^1+0*2^0+1*2^-1+1*2^-2=
4+2+0+0.5+0.25=6.75
還多多種進位制
舉例:R進位制 (R 代表任意數)
R=10 0-9
R=2 0-1
R=8 0-7
R=16 0- F
各種R進位制的數轉化為10進位制的數
舉例:
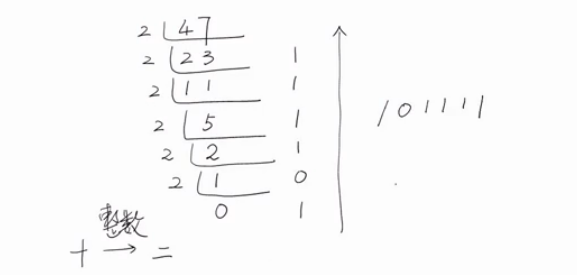
10進位制轉化為2進位制
除2取餘法.終止條件是商為0
小數轉換