求陣列的連續子陣列之和的最大值(一維二維)
阿新 • • 發佈:2019-02-08
求陣列的連續子陣列之和的最大值
輸入一個N個元素的整型陣列,數組裡有正數也有負數。陣列中連續的一個或多個整陣列成一個子陣列,每個子陣列都有一個和。求所有子陣列的和的最大值。 例如輸入的陣列為-9 -3 -2 2 -1 2 5 -7 1 5,和最大的子陣列為2 -1 2 5。因此輸出為該子陣列的和8。 可是如果都是負數的話,要返回0?還是返回最小的負數?,這個數時候你要問問面試官(交流很重要)。 OK,想一想該如何做?遍歷?遍歷是最偉大的方法,幾乎多有的題目都可解答,堪稱萬能解題法。 好吧,咱就先用遍歷來解決一下。Sum[i-j]代表i-j元素的和,需要N次遍歷,每一次遍歷都要求Sum[i-j]。 編碼開始
int MaxSum(int array[],int start,int end) { int MaxSum=-INFINITY;//最大值初始化為極小值 int sum=0; for(int i=start;i<=end;i++) { sum=0; //記得每次初始化,我們求的是子陣列的和 for(int j=i;j<=end;j++) { sum+=array[j]; if(sum>MaxSum) MaxSum=sum; } } return MaxSum; }
時間複雜度是O(n^2)。還湊合吧,還能繼續優化嗎? 想一想,之前學過的方法。分治法,分而治之,可以嗎?YES 如果我們把陣列array[1-N]分成兩部分array[0-N/2-1]和array[N/2-N-1],那麼我們要求的連續子陣列最大和就有了3種可能: 1 原始陣列最大和就是array[0-N/2-1]陣列的最大和 2 原始陣列最大和就是array[N/2-N-1]陣列的最大和 3 最大和的子陣列是包括array[N/2-1]和array[N/2]的一段子陣列。 前兩種情況可以用遞迴解決,第三種情況從Mid向兩邊遍歷一次O(n)就可以了。
遞迴要遞迴到只有一個元素的時候直接返回即可。時間複雜度很明顯是O(nlgn)。 編碼實現:
int MaxSum(int array[],int start,int end)
{
int LeftSum,RightSum,MidLeftSum,MidRightSum;
int max,sum;
int i;
if(end==start)
return array[start];
int pivot=start+(end-start)/2;
LeftSum=MaxSum(array,start,pivot);
RightSum=MaxSum(array,pivot+1,end);
max=-INFINITY; //最大值初始化為極小值
sum=0;
for(i=(end-start+1)/2-1;i>=start;i--) //求以array[N/2-1]結尾的一段最大和
{
sum+=array[i];
if(sum>max)
max=sum;
}
MidLeftSum=max;
max=-INFINITY;
sum=0;
for(i=(end-start+1)/2;i<=end;i++) //求以array[N/2]開始的一段最大和
{
sum+=array[i];
if(sum>max)
max=sum;
}
MidRightSum=max;
return Max(LeftSum,MidLeftSum+MidRightSum,RightSum);
}時間複雜度降到了O(nlgn),還不錯。可是我們不能僅僅滿足於這樣的複雜度,O(n)才是我們追求的目標。可是這個題目可以達到嗎? 想一想,這個題目有什麼性質? 最優子結構?YES。原陣列的最優解包含子陣列的最優解。陣列array[0-N-1]的最優解肯定包含子陣列array[1-N-1]的最優解。陣列array[0-N-1]的最優解與誰有關係?要麼是array[0],要麼是子陣列array[1-N-1]的最優解,要麼是兩者之和。而且在求最大和的時候會出現很多的重疊子問題。比如求array[0-N-1]和array[1-N-1]的最優解肯定都要求array[2-N-1]的最優解。而且滿足無後效性,對於當前求得array[0-N-1]的最優解只和array[1-N-1]的最優解有關係,和array[1-N-1]的值沒有關係,唯一影響的就是array[0]。 這樣我們就知道可以用DP來做。
假設用陣列All[i]表示array[i-N-1]的最大和,用陣列Start[i]表示包含arry[i]的array[i-N-1]的最大和。那我們要求array[i-N-1]的最大值就是All[i],Start[i],array[i]三者中的最大值。而Start[i]如何求呢?要麼等於array[i],要麼等於array[i]+Start[i+1]。而All[i]要麼和array[i]有關係要麼沒關係,所以要麼等於Start[i],,要麼等於All[i+1]。 這樣狀態轉移方程就來了: Start[i]=MaxNum(array[i],array[i]+Start[i+1]); All[i]=MaxNum(Start[i],All[i+1]); 我們要求的最大值就是All[0]。 編碼開始
int MaxSum(int array[],int start,int end)
{
int arraylength=end-start+1;
int *Start=new int[arraylength];
int *All=new int[arraylength];
Start[arraylength-1]=array[end]; //注意arraylength-1=end不是什麼時候都成立的//
All[arraylength-1]=array[end];
for(int i=end-1;i>=start;i--)
{
Start[i]=MaxNum(array[i],array[i]+Start[i+1]);
All[i]=MaxNum(Start[i],All[i+1]);
}
return All[0];
}時間複雜度當然是O(n)。因為我們有O(n)個子問題(array[0-i]),對於每一子問題我們有3種選擇。 這樣就演算法就比較nice了。可是空間複雜度很大啊,輔助空間就要O(n)。可以降低嗎?仔細分析下剛才所寫的程式碼,你能發現什麼問題嗎? 沒必要定義輔助陣列?YES。因為我們最後要求的只是陣列中的一個值。我們只要求這三個array[i],rray[i]+Start[i+1],All[i+1]的最大值即可,很多值就是一個過渡,一個變數足以解決問題。
程式碼修改
int MaxSum(int array[],int start,int end)
{
int Start,All;
Start=array[end];
All=array[end];
for(int i=end-1;i>=start;i--)
{
Start=MaxNum(array[i],array[i]+Start);
All=MaxNum(Start,All);
}
return All;
}輔助空間是O(1)。很不錯
可是我們可以換個寫法,如果Start[i]<0那就沒必要要他了,直接捨棄。
int MaxSum(int array[],int start,int end)
{
int Start,All;
Start=array[end];
All=array[end];
for(int i=end-1;i>=start;i--)
{
if(Start>=0)
Start+=array[i];
else
Start=array[i];
if(Start>All)
All=Start;
}
return All;
}測試程式碼
#include <iostream>
using namespace std;
const int N=10;
const int INFINITY=1000;//定義一個最大值
//求陣列的連續子陣列之和的最大值
int MaxSum(int array[],int start,int end);
int MaxNum(int x,int y);
int Max(int x,int y,int z);
int main()
{
int i;
int array[N]={-9,-3,-2,-2,-1,-2,-5,-7,-1,-5};
for(i=0;i<N;i++)
cout<<array[i]<<" ";
cout<<endl;
cout<<"連續子陣列之和的最大值MaxSum="<<MaxSum(array,0,N-1)<<endl;
return 0;
}OK,這樣才算是完美解決。 可是,這個時候我要問你,如果一維陣列首尾相連怎麼辦?
這個時候要分情況了,如果最優解沒有跨過array[N-1]到array[0],那就是原問題的解。如果跨過,那麼我們要遍歷一次就可以了。Sum=array[i]+....+array[N-1]+array[0]+...array[j],是嗎?這個時候我們還要判斷i和j的大小。如果i<=j那我們要求的就是 Sum=array[0]+....+array[N-1],否則Sum=array[0]+...array[j]+array[i]+....+array[N-1]。這個程式碼應該很好寫,因為有了剛才的鋪墊。 這個時候我再問你,如果我要返回下標,你要怎麼做?無非是傳入兩個座標值,每次求最大和的時候記錄下來即可。沒問題的。程式碼就不寫了。
OK,一維陣列咱算是說完了,那咱來看看二維的怎麼搞? 二維陣列連續的二維子陣列的和怎麼求,肯定是一個矩形,我們要遍歷嗎??? 遍歷的話估計複雜度扛不住吧。。如何遍歷也是一個問題。
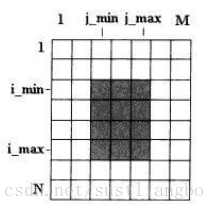
這個時候我們可以把每一行看成是一個元素,這樣就變成了一個縱向的一維陣列了。
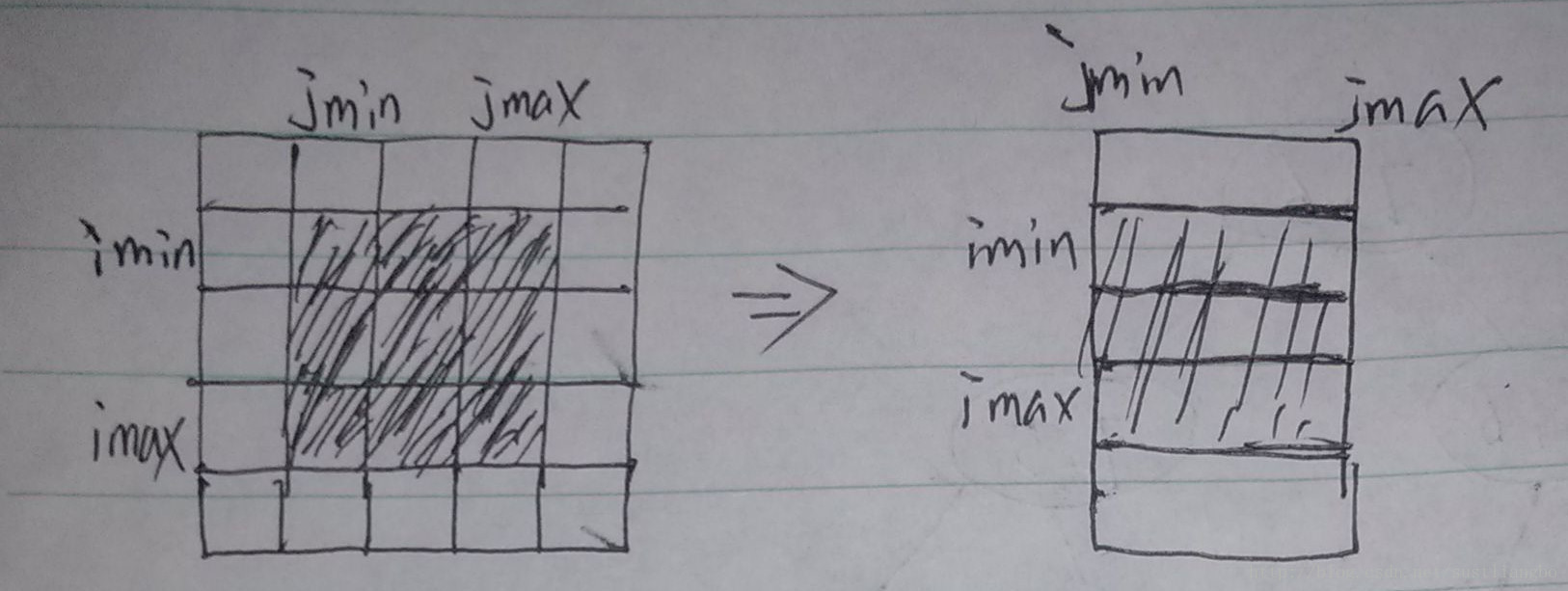
這樣對一維陣列的遍歷是和剛才一樣的。而對於每一行我們遍歷也是和一維是一樣的。編碼試一試
//求二維陣列的連續子陣列之和的最大值
int MaxSum(int (*array)[N])
{
int i,j;
int MaxSum=-INFINITY;//初始化
int imin,imax,jmin,jmax;
for(imin=1;imin<=N;imin++)
{
for(imax=imin;imax<=N;imax++)//當成是遍歷縱向的一維
{
for(jmin=1;jmin<=M;jmin++)
{
for(jmax=jmin;jmax<=M;jmax++)//當成是遍歷橫向的一維
MaxSum=MaxNum(MaxSum,PartSum(imin,jmin,imax,jmax));
}
}
}
return MaxSum;
}時間複雜度(N^2*M^2*O(PartSum)),如何求部分和PartSum呢?如果這個還是要遍歷求的話,複雜度真是不敢看了。。 求一維的時候我們求Sum[i-j]很好求,可是求二維的時候就變成了四個座標了,不敢遍歷求和了。我們可以先求部分和,把他當作已知的,這個時候遍歷求的時候複雜度就是O(1)。 如何求?我們定義一個部分和陣列PartSum,其中PartSum[i][[j]代表了下標(0,0),(0,j),(i,0),(i,j)包圍的區間的和。
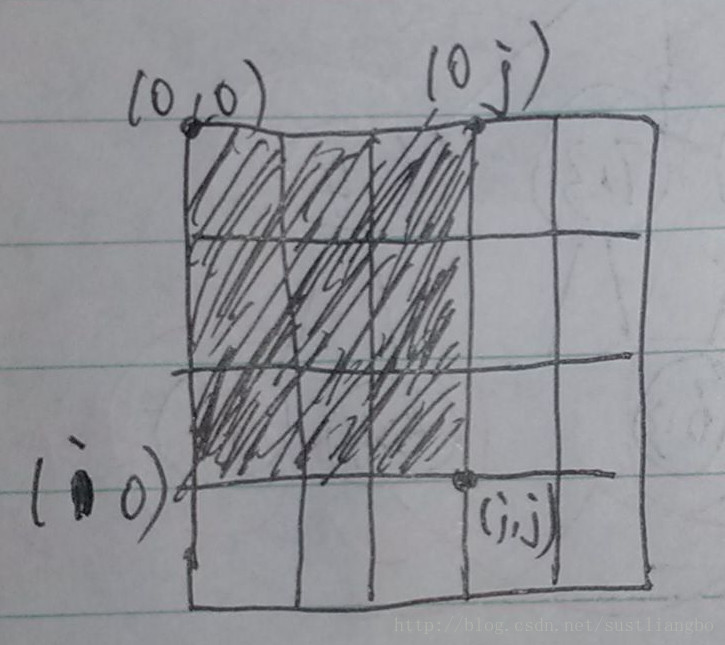
而此時下標(imin,jmin),(imin,jmax),(imax,jmin),(imax,jmax)包圍的區間和就等於
PartSum[imax][[jmax]-PartSum[imin-1][[jmax]-PartSum[imax][[jmin-1]+PartSum[imin-1][[jmin-1]。
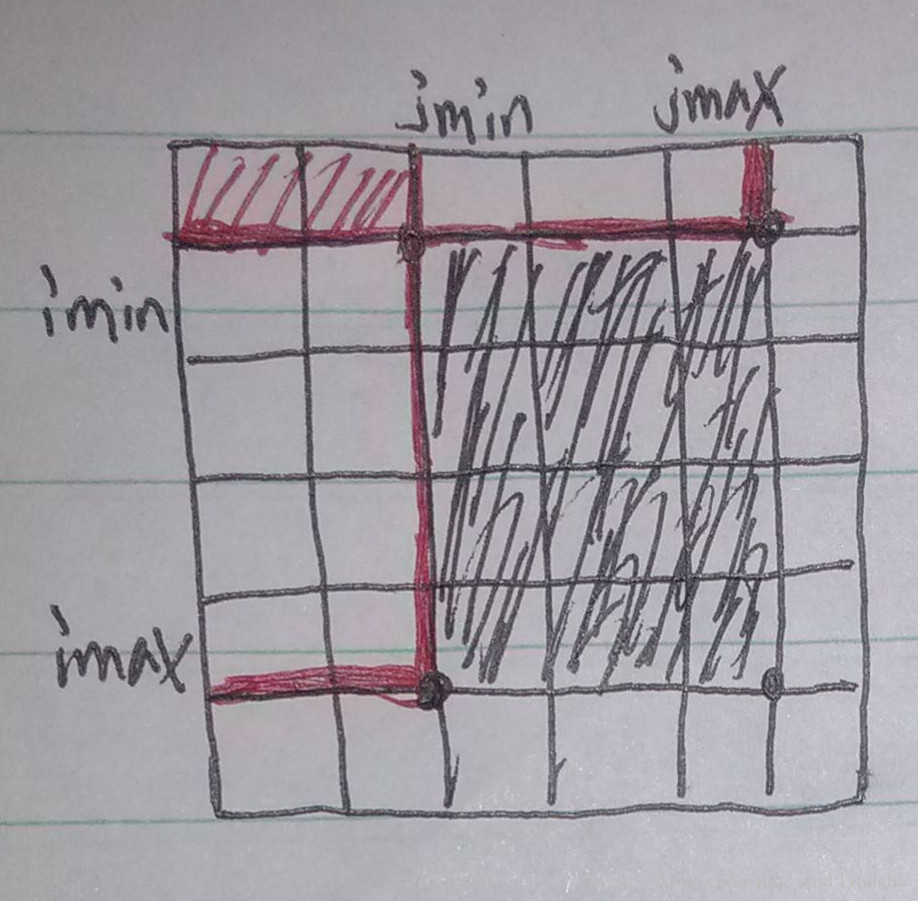
這就是我們要求的PartSum(imin,jmin,imax,jmax),接下來就是求PartSum陣列了。如何求呢?
對於每一個PartSum[i][[j]都不是孤立的,都是和其他的有關係的。我們要找出這個關係式
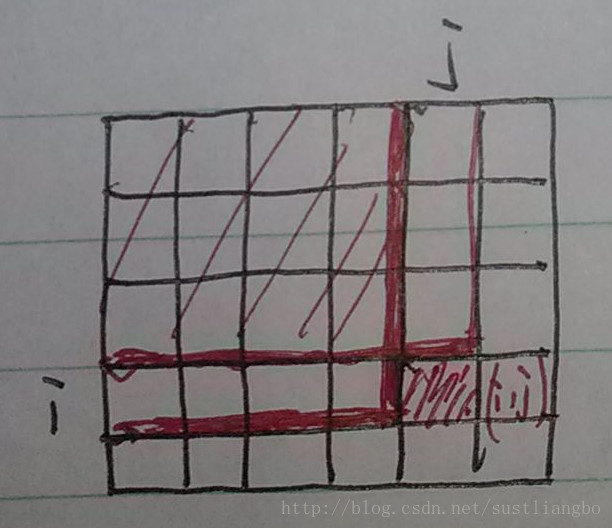
PartSum[i][[j]=PartSum[i-1][[j]+PartSum[i][[j-1]-PartSum[i-1][[j-1]+array[i][j]。 這樣求可以求出全部的PartSum[i][[j],可是我們不要忽略了一點,PartSum[0][[0]=?對於邊界值我們要處理好,而且下標要從1開始。對於PartSum[i][[0]和PartSum[0][[j]都要初始化0,而且array[i][j]的下標也是要-1,因為陣列的下標是從0開始的。這是一個辦法,不過我們也可以單獨求PartSum[i][[0]和PartSum[0][[j]的值,連續相加即可,然後再求其他的也是可以的,空間複雜度也是一樣。可是在4重遍歷的時候對於PartSum[i][[0]和PartSum[0][[j]我們還是要另外處理,這就比較麻煩了。我們還是用預處理的方法來編碼吧。。
int PartSum[N+1][M+1];
int i,j;
for(i=0;i<=N;i++)
PartSum[i][0]=0;
for(j=0;j<=M;j++)
PartSum[0][j]=0;
for(i=1;i<=N;i++)
for(j=1;j<=M;j++)
PartSum[i][j]=PartSum[i-1][j]+PartSum[i][j-1]-PartSum[i-1][j-1]+array[i-1][j-1];OK,求得部分和之後我們就開始完善我們的編碼了。記住一點,下標(imin,jmin),(imin,jmax),(imax,jmin),(imax,jmax)包圍的區間和等於
PartSum[imax][[jmax]-PartSum[imin-1][[jmax]-PartSum[imax][[jmin-1]+PartSum[imin-1][[jmin-1]。編碼開始:
//求二維陣列的連續子陣列之和的最大值
int MaxSum(int (*array)[N])
{
int PartSum[N+1][M+1];
int i,j;
for(i=0;i<=N;i++)
PartSum[i][0]=0;
for(j=0;j<=M;j++)
PartSum[0][j]=0;
for(i=1;i<=N;i++)
for(j=1;j<=M;j++)
PartSum[i][j]=PartSum[i-1][j]+PartSum[i][j-1]-PartSum[i-1][j-1]+array[i-1][j-1];
int MaxSum=-INFINITY;//初始化
int imin,imax,jmin,jmax;
for(imin=1;imin<=N;imin++)
for(imax=imin;imax<=N;imax++)
for(jmin=1;jmin<=M;jmin++)
for(jmax=jmin;jmax<=M;jmax++)
MaxSum=MaxNum(MaxSum,PartSum[imax][jmax]-PartSum[imin-1][jmax]-PartSum[imax][jmin-1]+PartSum[imin-1][jmin-1]);
return MaxSum;
}時間複雜度是O(N^2*M^2),有點坑啊。想一想一維的時候我們用DP來做,這個也可以嗎?可以的。我們把每一列看成一個元素。這樣對於遍歷的行區間,我們就可以當成一維來做。
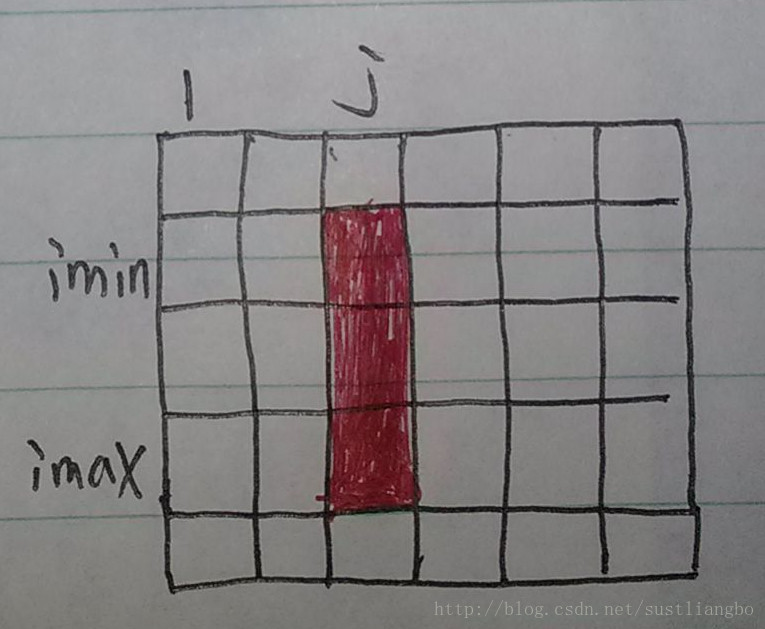
對於imin和imax之間的每一列,就相當於一維的一個元素。
假設這個一維陣列是BC,則BC[j]=array[imin][j]+....+array[imax][j],問題就變成了求BC陣列的連續子陣列之和的最大值了。而根據剛才求的部分和,我們可以知道對於imin行和imax行之間的區間第j列的值是
BC(PartSum,imin,imax,j)=PartSum[imax][j]-PartSum[imin-1][j]-PartSum[imax][j-1]+PartSum[imin-1][j-1].(此時BC是一個函式)
OK,編碼開始
//求二維陣列的連續子陣列之和的最大值
int MaxSum(int (*array)[N])
{
int PartSum[N+1][M+1];
int i,j;
for(i=0;i<=N;i++)
PartSum[i][0]=0;
for(j=0;j<=M;j++)
PartSum[0][j]=0;
for(i=1;i<=N;i++)
for(j=1;j<=M;j++)
PartSum[i][j]=PartSum[i-1][j]+PartSum[i][j-1]-PartSum[i-1][j-1]+array[i-1][j-1];
int MaxSum=-INFINITY;
int Start,All;
int imin,imax;
for(imin=1;imin<=N;imin++)
{
for(imax=imin;imax<=N;imax++)
{
Start=BC(PartSum,imin,imax,M);
All=BC(PartSum,imin,imax,M);
for(j=M-1;j>=1;j--)
{
if(Start>0)
Start+=BC(PartSum,imin,imax,j);
else
Start=BC(PartSum,imin,imax,j);
if(Start>All)
All=Start;
}
if(All>MaxSum)
MaxSum=All;
}
}
return MaxSum;
}
int BC(int (*PartSum)[N+1],int imin,int imax,int j) //imin--imax第j列的和
{
int value;
value=PartSum[imax][j]-PartSum[imin-1][j]-PartSum[imax][j-1]+PartSum[imin-1][j-1];
return value;
}OK,very nice.時間輔助度降到O(N*M*min(M,N)),差不多O(N^3)吧。
這個時候我要問你,如果也把二維的陣列首尾相連,你要怎麼求最大值。方法和一維的類似,略有不同吧。
如果對於三維陣列求一個長方體的最大和,你怎麼求?
如果上下也相連怎麼辦???
四維呢??
這次你可要好好思考了。先說到這吧。
轉載請註明出處http://blog.csdn.net/sustliangbo/article/details/9411335
