前面我們在是實現K-means演算法的時候，提到了它本身存在的缺陷：

1.可能收斂到區域性最小值
2.在大規模資料集上收斂較慢

對於上一篇博文最後說的，當陷入區域性最小值的時候，處理方法就是多執行幾次K-means演算法，然後選擇畸變函式J較小的作為最佳聚類結果。這樣的說法顯然不能讓我們接受，我們追求的應該是一次就能給出接近最優的聚類結果。

其實K-means的缺點的根本原因就是：對K個質心的初始選取比較敏感。質心選取得不好很有可能就會陷入區域性最小值。

基於以上情況，有人提出了二分K-means演算法來解決這種情況，也就是弱化初始質心的選取對最終聚類效果的影響。

二分K-means演算法

在介紹二分K-means演算法之前我們先說明一個定義：SSE（Sum of Squared Error）,也就是誤差平方和，它是用來度量聚類效果的一個指標。其實SSE也就是我們在K-means演算法中所說的畸變函式：

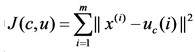
SSE計算的就是一個cluster中的每個點到質心的平方差，它可以度量聚類的好壞。顯然SSE越小，說明聚類效果越好。

二分K-means演算法的主要思想：
首先將所有點作為一個簇，然後將該簇一分為二。之後選擇能最大程度降低聚類代價函式（也就是誤差平方和）的簇劃分為兩個簇。以此進行下去，直到簇的數目等於使用者給定的數目k為止。

二分k均值演算法的虛擬碼如下：

將所有資料點看成一個簇

    當簇數目小於k時

      對每一個簇

          計算總誤差

          在給定的簇上面進行k-均值聚類（k=2）

          計算將該簇一分為二後的總誤差

      選擇使得誤差最小的那個簇進行劃分操作
 

Matlab 實現

function bikMeans
%%
clc
clear
close all
%%
biK = 4;
biDataSet = load('testSet.txt');
[row,col] = size(biDataSet);
% 儲存質心矩陣
biCentSet = zeros(biK,col);
% 初始化設定cluster數量為1
numCluster = 1;
%第一列儲存每個點被分配的質心，第二列儲存點到質心的距離
biClusterAssume = zeros(row,2);
%初始化質心
biCentSet(1,:) = mean(biDataSet)
for
 
 i = 1:row
    biClusterAssume(i,1) = numCluster;
    biClusterAssume(i,2) = distEclud(biDataSet(i,:),biCentSet(1,:));
end
while numCluster < biK
    minSSE = 10000;
    %尋找對哪個cluster進行劃分最好，也就是尋找SSE最小的那個cluster
    for j = 1:numCluster
        curCluster = biDataSet(find(biClusterAssume(:,1) == j),:);
        [spiltCentSet,spiltClusterAssume] = kMeans(curCluster,2);
        spiltSSE = sum(spiltClusterAssume(:,2));
        noSpiltSSE = sum(biClusterAssume(find(biClusterAssume(:,1)~=j),2));
        curSSE = spiltSSE + noSpiltSSE;
        fprintf('第%d個cluster被劃分後的誤差為：%f \n' , [j, curSSE])
        if (curSSE < minSSE)
            minSSE = curSSE;
            bestClusterToSpilt = j;
            bestClusterAssume = spiltClusterAssume;
            bestCentSet = spiltCentSet;
        end
    end
    bestClusterToSpilt
    bestCentSet
     %更新cluster的數目
    numCluster = numCluster + 1;
    bestClusterAssume(find(bestClusterAssume(:,1) == 1),1) = bestClusterToSpilt;
    bestClusterAssume(find(bestClusterAssume(:,1) == 2),1) = numCluster;
    % 更新和新增質心座標
    biCentSet(bestClusterToSpilt,:) = bestCentSet(1,:);
    biCentSet(numCluster,:) = bestCentSet(2,:);
    biCentSet
    % 更新被劃分的cluster的每個點的質心分配以及誤差
    biClusterAssume(find(biClusterAssume(:,1) == bestClusterToSpilt),:) = bestClusterAssume;
end

figure
%scatter(dataSet(:,1),dataSet(:,2),5)
for i = 1:biK
    pointCluster = find(biClusterAssume(:,1) == i);
    scatter(biDataSet(pointCluster,1),biDataSet(pointCluster,2),5)
    hold on
end
%hold on
scatter(biCentSet(:,1),biCentSet(:,2),300,'+')
hold off

end

% 計算歐式距離
function dist = distEclud(vecA,vecB)
    dist  = sum(power((vecA-vecB),2));
end

% K-means演算法
function [centSet,clusterAssment] = kMeans(dataSet,K)

[row,col] = size(dataSet);
% 儲存質心矩陣
centSet = zeros(K,col);
% 隨機初始化質心
for i= 1:col
    minV = min(dataSet(:,i));
    rangV = max(dataSet(:,i)) - minV;
    centSet(:,i) = repmat(minV,[K,1]) + rangV*rand(K,1);
end

% 用於儲存每個點被分配的cluster以及到質心的距離
clusterAssment = zeros(row,2);
clusterChange = true;
while clusterChange
    clusterChange = false;
    % 計算每個點應該被分配的cluster
    for i = 1:row
        % 這部分可能可以優化
        minDist = 10000;
        minIndex = 0;
        for j = 1:K
            distCal = distEclud(dataSet(i,:) , centSet(j,:));
            if (distCal < minDist)
                minDist = distCal;
                minIndex = j;
            end
        end
        if minIndex ~= clusterAssment(i,1)            
            clusterChange = true;
        end
        clusterAssment(i,1) = minIndex;
        clusterAssment(i,2) = minDist;
    end

    % 更新每個cluster 的質心
    for j = 1:K
        simpleCluster = find(clusterAssment(:,1) == j);
        centSet(j,:) = mean(dataSet(simpleCluster',:));
    end
end
end

演算法迭代過程如下

biCentSet =

-0.1036    0.0543
     0         0
     0         0
     0         0

第1個cluster被劃分後的誤差為：792.916857

bestClusterToSpilt =

 1

bestCentSet =

   -0.2897   -2.8394
    0.0825    2.9480

biCentSet =

   -0.2897   -2.8394
    0.0825    2.9480
     0         0
     0         0

第1個cluster被劃分後的誤差為：409.871545
第2個cluster被劃分後的誤差為：532.999616

bestClusterToSpilt =

 1

bestCentSet =

   -3.3824   -2.9473
    2.8029   -2.7315

biCentSet =

   -3.3824   -2.9473
    0.0825    2.9480
    2.8029   -2.7315
     0         0

第1個cluster被劃分後的誤差為：395.669052
第2個cluster被劃分後的誤差為：149.954305
第3個cluster被劃分後的誤差為：393.431098

bestClusterToSpilt =

 2

bestCentSet =

2.6265    3.1087
-2.4615    2.7874

biCentSet =

   -3.3824   -2.9473
    2.6265    3.1087
    2.8029   -2.7315
   -2.4615    2.7874

最終效果圖

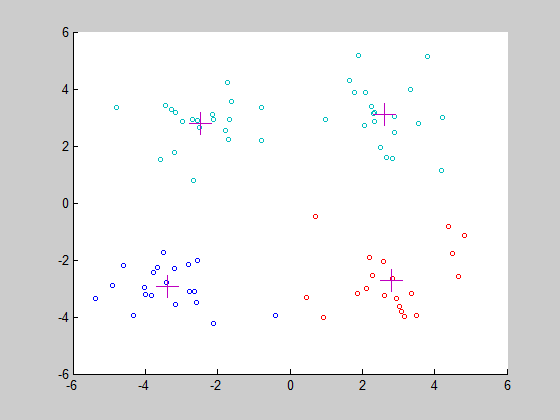
運用二分K-means演算法進行聚類的時候，不同的初始質心聚類結果還是會稍微有點不同，因為實際上這也只是弱化隨機質心對聚類結果的影響而已，並不能消除其影響，不過最終還是能收斂到全域性最小。

程式碼和資料已經存放在 GitHub 上，可以提供下載，如果覺得有用請給個star吧。