計數排序——JAVA實現
計數排序是一種演算法複雜度 O(n) 的排序方法,適合於小範圍集合的排序。比如100萬學生參加高考,我們想對這100萬學生的數學成績(假設分數為0到100)做個排序。我們如何設計一個最高效的排序演算法。本文不光給出計數排序演算法的傳統寫法,還將一步步深入討論演算法的優化,直到時間複雜度和空間複雜度最優。
先看看計數排序的定義
Counting sort (sometimes referred to as ultra sort or math sort[1])
is a sorting algorithm which (like bucket
sort) takes advantage of knowing the
計數排序是一個類似於桶排序的排序演算法,其優勢是對已知數量範圍的陣列進行排序。它建立一個長度為這個資料範圍的陣列C,C中每個元素記錄要排序陣列中對應記錄的出現個數。這個演算法於1954年由 Harold H. Seward 提出。
下面以示例來說明這個演算法
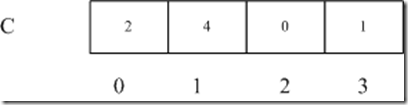
假設要排序的陣列為 A = {1,0,3,1,0,1,1}
這裡最大值為3,最小值為0,那麼我們建立一個數組C,長度為4.
然後一趟掃描陣列A,得到A中各個元素的總數,並保持到陣列C的對應單元中。
比如0 的出現次數為2次,則 C[0] = 2;1 的出現次數為4次,則C[1] = 4
由於C 是以A的元素為下標的,所以這樣一做,A中的元素在C中自然就成為有序的了,這裡我們可以知道 順序為 0,1,3 (2 的計數為0)
然後我們把這個在C中的記錄按每個元素的計數展開到輸出陣列B中,排序就完成了。
也就是 B[0] 到 B[1] 為0 B[2] 到 B[5] 為1 這樣依此類推。
這種排序演算法,依靠一個輔助陣列來實現,不基於比較,演算法複雜度為 O(n) ,但由於要一個輔助陣列C,所以空間複雜度要大一些,由於計算機的記憶體有限,這種演算法不適合範圍很大的數的排序。
注:基於比較的排序演算法的最佳平均時間複雜度為 O(nlogn)
Counting sort
Depends on a key assumption: numbers to be sorted are integers in{0, 1, . . . , k}.
Input: A[1 . . n], where A[ j ] ∈ {0, 1, . . . , k} for j = 1, 2, . . . , n. Array A and
values n and k are given as parameters.
Output: B[1 . . n], sorted. B is assumed to be already allocated and is given as a
parameter.
Auxiliary storage: C[0 . . k]
8-4 Lecture Notes for Chapter 8: Sorting in Linear Time
COUNTING-SORT(A, B, n, k)
for i ← 0 to k
do C[i ] ← 0
for j ← 1 to n
do C[A[ j ]] ← C[A[ j ]] + 1
for i ← 1 to k
do C[i ] ← C[i ] + C[i − 1]
for j ← n downto 1
do B[C[A[ j ]]] ← A[ j ]
C[A[ j ]] ← C[A[ j ]] − 1
Do an example for A = 21, 51, 31, 01, 22, 32, 02, 33
Counting sort is stable (keys with same value appear in same order in output as
they did in input) because of how the last loop works.
上面這段引自麻省理工大學計算機演算法教材的技術排序部分,我不做翻譯了。這個就是這個演算法的典型解法,我把它作為方案1.
這個演算法的實際掃描次數為 n+k (不包括寫的次數)
方案1
public static void Sort(int[] A, out int[] B, int k)
{
Debug.Assert(k > 0);
Debug.Assert(A != null);
int[] C = new int[k + 1];
B = new int[A.Length];
for (int j = 0; j < A.Length; j++)
{
C[A[j]]++;
}
for (int i = 1; i <= k; i++)
{
C[i] += C[i-1];
}
for (int j = A.Length - 1; j >= 0; j--)
{
B[C[A[j]]-1] = A[j];
C[A[j]]--;
}
}
上面程式碼是方案1 的解法,也是計數排序演算法的經典解法,麻省的教材上也是這樣解。不過這個解法並不是最優的,因為空間複雜度還應該可以優化,我們完全可以不要那個輸出的陣列B,直接對A進行排序。在繼續看方案2之前,我建議大家先自己思考一下,看看是否有辦法省略掉陣列B
方案2
我們對上述程式碼進行優化
public static void Sort(int[] A, int k)
{
Debug.Assert(k > 0);
Debug.Assert(A != null);
int[] C = new int[k + 1];
for (int j = 0; j < A.Length; j++)
{
C[A[j]]++;
}
int z = 0;
for (int i = 0; i <= k; i++)
{
while (C[i]-- > 0)
{
A[z++] = i;
}
}
}由於C陣列下標 i 就是A 的值,所以我們不需要保留A中原來的數了,這個程式碼減少了一個數組B,而且要比原來的程式碼簡化了很多。
和快速排序的速度比較
拿本文剛開始那個高考成績的例子來做
int[] A = new int[1000000];
int[] B = new int[1000000];
Random rand = new Random();
for (int i = 0; i < A.Length; i++)
{
A[i] = rand.Next(0, 100);
}
A.CopyTo(B, 0);
Stopwatch sw = new Stopwatch();
sw.Start();
Array.Sort(B);
sw.Stop();
Console.WriteLine(sw.ElapsedMilliseconds);
sw.Reset();
sw.Start();
CountingSort.Sort(A, 100);
sw.Stop();
Console.WriteLine(sw.ElapsedMilliseconds);
輸出結果
134 //快速排序
18 //計數排序
可見計數排序要比快速排序快將近6倍左右。