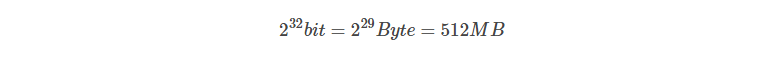5TB的硬碟上放滿了資料，請寫一個演算法將這些資料進行排重。如果這些資料是一些32bit大小的資料該如何解決？如果是64bit的呢？

在面試時遇到的問題，問題的解決方案十分典型，但對於海量資料處理接觸少的同學可能一時也想不到什麼好方案。介紹兩個演算法，對於空間的利用到達了一種極致，那就是Bitmap和布隆過濾器(Bloom Filter)。

Bitmap演算法

在網上並沒有找到Bitmap演算法的中文翻譯，在《程式設計珠璣》中有提及。與其說是演算法，不如說是一種緊湊的資料儲存結構。其實如果並非如此大量的資料，有很多排重方案可以使用，典型的就是雜湊表。

public int[] removeDuplicates(int[] array) {
    int index = 0;
    Map<Integer, Boolean> maps = new LinkedHashMap<Integer, Boolean>();
    for(int num : array) {
        if(!maps.contains(num)) {
            array[index] = num;
            index++;
            maps.put(num, true);
        }
    }

    return newArray;
}
 

實際上，雜湊表實際上為每一個可能出現的數字提供了一個一一對映的關係，每個元素都相當於有了自己的獨享的一份空間，這個對映由雜湊函式來提供（這裡我們先不考慮碰撞）。實際上雜湊表甚至還能記錄每個元素出現的次數，這樣的資料結構完成這個任務有點“大材小用”了。

我們拆解一下我們的需求：

1. 集合中每個元素（示例中是int）有一個獨享的空間
2. 找到一個到這個空間的對映方法

這個空間要多大？對於我們的問題來說，一個boolean就夠了，或者說，1個bit就夠了，我們只想知道某個元素出現過沒有。如果為每個所有可能的值分配1個bit，32bit的int所有可能取值需要記憶體空間為：

那怎麼樣完成這個對映呢？其實就是Bitmap所要完成的工作了。如果我們把整型0x01、0x02、…、0x08的空間依次對映到一個Byte上，每個bit就代表這個int

值是否出現過，初值為0（false）。

若擴充套件到整個int取值域，申請一個byte[]即可，示例程式碼如下：

public static final int _1MB = 1024 * 1024;

public static byte[] flags = new byte[ 512 * _1MB ];


public static void main(String[] args) {

    int[] array = {255, 1024, 0, 65536}

    int index = 0;
    for(int num : array) {
        if(!getFlags(num)) {
            //未出現的元素
            array[index] = num;
            index = index + 1;
            //設定標誌位
            setFlags(num);
        }
    }
}

public static void setFlags(int num) {
    flags[num >> 3] |= 0x01 << (num & (0x07));
}

public static boolean getFlags(int num) {
    return flags[num >> 3] >> (num & (0x07)) & 0x01;
}
 

其實，就是按int從小到大的順序依次擺放到byte[]中，僅涉及到一些除以2的整次冪和對2的整次冪取餘的位操作小技巧。很顯然，對於小資料量、資料取值很稀疏，上面的方法並沒有什麼優勢，但對於海量的、取值分佈很均勻的集合進行去重，Bitmap極大地壓縮了所需要的記憶體空間。於此同時，還額外地完成了對原始陣列的排序工作。缺點是，Bitmap對於每個元素只能記錄1bit資訊，如果還想完成額外的功能，恐怕只能靠犧牲更多的空間、時間來完成了。

雜湊 hash

原理

Hash （雜湊，或者雜湊）函式在計算機領域，尤其是資料快速查詢領域，加密領域用的極廣。

其作用是將一個大的資料集對映到一個小的資料集上面（這些小的資料集叫做雜湊值，或者雜湊值）。

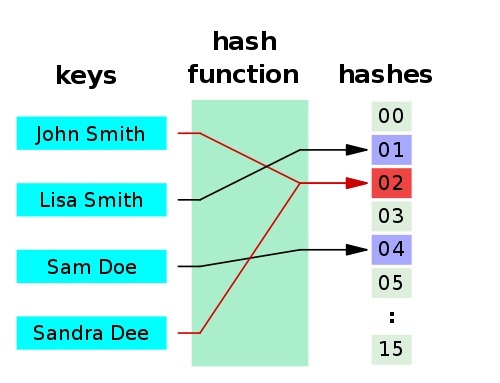
一個應用是Hash table（散列表，也叫雜湊表），是根據雜湊值 (Key value) 而直接進行訪問的資料結構。也就是說，它通過把雜湊值對映到表中一個位置來訪問記錄，以加快查詢的速度。下面是一個典型的 hash 函式 / 表示意圖：

雜湊函式有以下兩個特點：

• 如果兩個雜湊值是不相同的（根據同一函式），那麼這兩個雜湊值的原始輸入也是不相同的。
• 雜湊函式的輸入和輸出不是唯一對應關係的，如果兩個雜湊值相同，兩個輸入值很可能是相同的。但也可能不同，這種情況稱為 “雜湊碰撞”（或者 “雜湊衝突”）。

缺點： 引用吳軍博士的《數學之美》中所言，雜湊表的空間效率還是不夠高。如果用雜湊表儲存一億個垃圾郵件地址，每個email地址 對應 8bytes, 而雜湊表的儲存效率一般只有50%，因此一個email地址需要佔用16bytes. 因此一億個email地址佔用1.6GB，如果儲存幾十億個email address則需要上百GB的記憶體。除非是超級計算機，一般的伺服器是無法儲存的。
所以要引入下面的 Bloom Filter。

布隆過濾器 Bloom Filter

原理

如果想判斷一個元素是不是在一個集合裡，一般想到的是將集合中所有元素儲存起來，然後通過比較確定。連結串列、樹、散列表（又叫雜湊表，Hash table）等等資料結構都是這種思路。但是隨著集合中元素的增加，我們需要的儲存空間越來越大。同時檢索速度也越來越慢。
Bloom Filter 是一種空間效率很高的隨機資料結構，Bloom filter 可以看做是對 bit-map 的擴充套件, 它的原理是：
當一個元素被加入集合時，通過 K 個 Hash 函式將這個元素對映成一個位陣列（Bit array）中的 K 個點，把它們置為 1。檢索時，我們只要看看這些點是不是都是 1 就（大約）知道集合中有沒有它了：

• 如果這些點有任何一個 0，則被檢索元素一定不在；
• 如果都是 1，則被檢索元素很可能在。

優點

它的優點是空間效率和查詢時間都遠遠超過一般的演算法，布隆過濾器儲存空間和插入 / 查詢時間都是常數O(k)。另外, 雜湊函式相互之間沒有關係，方便由硬體並行實現。布隆過濾器不需要儲存元素本身，在某些對保密要求非常嚴格的場合有優勢。

缺點

但是布隆過濾器的缺點和優點一樣明顯。誤算率是其中之一。隨著存入的元素數量增加，誤算率隨之增加。但是如果元素數量太少，則使用散列表足矣。
(誤判補救方法是：再建立一個小的白名單，儲存那些可能被誤判的資訊。)
另外，一般情況下不能從布隆過濾器中刪除元素. 我們很容易想到把位陣列變成整數陣列，每插入一個元素相應的計數器加 1, 這樣刪除元素時將計數器減掉就可以了。然而要保證安全地刪除元素並非如此簡單。首先我們必須保證刪除的元素的確在布隆過濾器裡面. 這一點單憑這個過濾器是無法保證的。另外計數器迴繞也會造成問題。

Example

可以快速且空間效率高的判斷一個元素是否屬於一個集合；用來實現資料字典，或者集合求交集。

如： Google chrome 瀏覽器使用bloom filter識別惡意連結（能夠用較少的儲存空間表示較大的資料集合，簡單的想就是把每一個URL都可以對映成為一個bit），這種方法效率非常高，並且誤判率在萬分之一以下。

又如： 檢測垃圾郵件

假定我們儲存一億個電子郵件地址，我們先建立一個十六億二進位制（位元），即兩億位元組的向量，然後將這十六億個二進位制全部設定為零。對於每一個電子郵件地址 X，我們用八個不同的隨機數產生器（F1,F2, ...,F8） 產生八個資訊指紋（f1, f2, ..., f8）。再用一個隨機數產生器 G 把這八個資訊指紋對映到 1 到十六億中的八個自然數 g1, g2, ...,g8。現在我們把這八個位置的二進位制全部設定為一。當我們對這一億個 email 地址都進行這樣的處理後。一個針對這些 email 地址的布隆過濾器就建成了。

再如此題：

A,B 兩個檔案，各存放 50 億條 URL，每條 URL 佔用 64 位元組，記憶體限制是 4G，讓你找出 A,B 檔案共同的 URL。如果是三個乃至 n 個檔案呢？

分析 ：如果允許有一定的錯誤率，可以使用 Bloom filter，4G 記憶體大概可以表示 340 億 bit。將其中一個檔案中的 url 使用 Bloom filter 對映為這 340 億 bit，然後挨個讀取另外一個檔案的 url，檢查是否與 Bloom filter，如果是，那麼該 url 應該是共同的 url（注意會有一定的錯誤率）。”