最近學習了左神BFPRT演算法，給大家先講個段子。

左神說他每次去美國面試，他都會拿BFPRT演算法吹一吹。美國5個大佬在一個美麗的地方研究出來這個演算法，他說自己熱愛演算法，他會BFPRT，每次去美國都會懷著朝聖的姿態去在那個地方轉轉。面試官一聽：哇！ 這麼厲害， 過！！！！！！！

好了，下來說說這個演算法。

BFPRT演算法是在進行大量資料排序求topk(前k個最大或最小的數）時最優演算法。

為什麼叫BFPRT演算法，因為是美國5個大佬搞出來的，所以分別取他們的名字命名演算法。

演算法步驟大概如下：

1  將陣列劃分區域，5個數為一組，把陣列分為若干組。（為什麼是5呢？因為5能更好的收斂時間複雜度。）

2  將分開的組進行組內排序（這裡我用的是插入排序），找出每組數的中位數。

3  找出的若干個中位數，單獨放一組進行排序。

4  在找出的中位陣列中，遞迴呼叫步驟2的過程，找出中位陣列的中位數，把這個中位數叫做劃分數。

5  用劃分數進行partition過程（類似於快速排序的每趟的劃分過程）：小於劃分數放左邊，等於劃分數放中間，大於劃分數放右邊。

6  將劃分數與k進行比較：

            k<劃分數，在步驟5的左邊區域遞迴上述過程，找出左邊區域的中位數與k比較，直到與k相等，最後的劃分數左邊就是前k小的數；

            k=劃分數，那麼左邊區域直接為前k小的數；

            k>劃分數，在步驟5的右邊區域遞迴上述過程，找出右邊區域的中位數與k比較，直到與k相等，最後的劃分數左邊就是前k小的數；

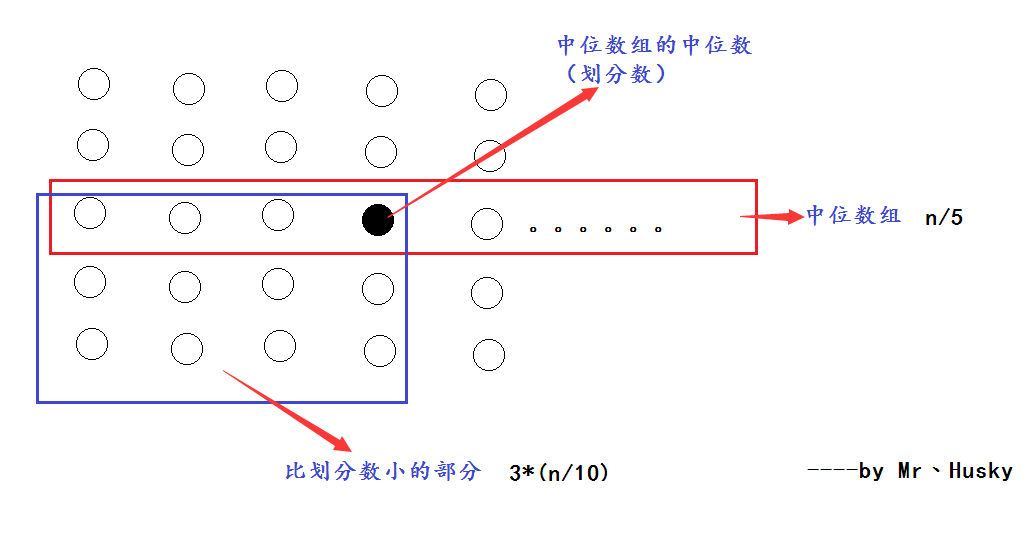
為什麼要花費這麼多步驟去尋找劃分數呢？假設陣列長度為n，那麼整個陣列一共有n/5箇中位數，在中位陣列找出中位陣列的中位數（劃分數），那麼就會有3*（n/10）個數比劃分數小-如圖紅色區域所示：

我們一次就可以至少刷掉3*（n/10）、最多7*（n/10）的數量級的資料進行遞迴排序，節省了很多時間！

程式碼實現如下所示：

package com.zuoshen;
/** 
 * BFPRT演算法求topk，時間複雜度bO(n)
 *
 * @author wanglongfei    
 * E-mail: 
 
[email protected]
 * @version 2017年8月5日
 * 
 */
public class BFPRT {
	
	    // 得到前k個最小的數
		public static int[] getMinKNumsByBFPRT(int[] arr, int k) {
			if (k < 1 || k > arr.length) {
				return arr;
			}
			int minKth = getMinKthByBFPRT(arr, k);
			int[] res = new int[k];//res前k個結果集
			int index = 0;
			
			for (int i = 0; i != arr.length; i++) {
				if (arr[i] < minKth) {
					res[index++] = arr[i];
				}
			}
			for (; index != res.length; index++) {
				res[index] = minKth;
			}
			return res;
		}
		
		
	   //找出比k小的前k個數
		public static int getMinKthByBFPRT(int[] arr, int K) {
			int[] copyArr = copyArray(arr);
			return select(copyArr, 0, copyArr.length - 1, K - 1);
		}
		
       //複製陣列
		public static int[] copyArray(int[] arr) {
			int[] res = new int[arr.length];
			for (int i = 0; i != res.length; i++) {
				res[i] = arr[i];
			}
			return res;
		}
		
		
	      //用劃分值與k相比，依次遞迴排序
		public static int select(int[] arr, int begin, int end, int i) {
			if (begin == end) { //begin陣列的開始 end陣列的結尾  i表示要求的第k個數
				return arr[begin];
			}
			int pivot = medianOfMedians(arr, begin, end);//找出劃分值（中位陣列中的中位數）
			int[] pivotRange = partition(arr, begin, end, pivot);
			if (i >= pivotRange[0] && i <= pivotRange[1]) {//小於放左邊，=放中間，大於放右邊
				return arr[i];
			} else if (i < pivotRange[0]) {
				return select(arr, begin, pivotRange[0] - 1, i);
			} else {
				return select(arr, pivotRange[1] + 1, end, i);
			}
		}
		
		
	     //找出中位陣列中的中位數  
		public static int medianOfMedians(int[] arr, int begin, int end) {
			int num = end - begin + 1;              
			int offset = num % 5 == 0 ? 0 : 1;       //分組:每組5個數，不滿5個單獨佔一組
			int[] mArr = new int[num / 5 + offset];  //mArr：中位陣列成的陣列
			for (int i = 0; i < mArr.length; i++) {  //計算分開後各陣列的開始位置beginI 結束位置endI
				int beginI = begin + i * 5;
				int endI = beginI + 4;
				mArr[i] = getMedian(arr, beginI, Math.min(end, endI));//對於最後一組（不滿5個數），結束位置要選擇end
			}
			return select(mArr, 0, mArr.length - 1, mArr.length / 2);
		}
		
	    //劃分過程，類似於快排
		public static int[] partition(int[] arr, int begin, int end, int pivotValue) {
			int small = begin - 1;
			int cur = begin;
			int big = end + 1;
			while (cur != big) {
				if (arr[cur] < pivotValue) {
					swap(arr, ++small, cur++);
				} else if (arr[cur] > pivotValue) {
					swap(arr, cur, --big);
				} else {
					cur++;
				}
			}
			int[] range = new int[2];
			range[0] = small + 1;//比劃分值小的範圍
			range[1] = big - 1;  //比劃分值大的範圍
			
			return range;
		}
		
		
	    //計算中位數
		public static int getMedian(int[] arr, int begin, int end) {
			insertionSort(arr, begin, end);//將陣列中的5個數排序
			int sum = end + begin;
			int mid = (sum / 2) + (sum % 2);
			return arr[mid];
		}
		
		
	    //陣列中5個數排序（插入排序）
		public static void insertionSort(int[] arr, int begin, int end) {
			for (int i = begin + 1; i != end + 1; i++) {
				for (int j = i; j != begin; j--) {
					if (arr[j - 1] > arr[j]) {
						swap(arr, j - 1, j);
					} else {
						break;
					}
				}
			}
		}
		
		
	    //交換元素順序
		public static void swap(int[] arr, int index1, int index2) {
			int tmp = arr[index1];
			arr[index1] = arr[index2];
			arr[index2] = tmp;
		}
		
		
        //列印結果
		public static void printArray(int[] arr) {
			for (int i = 0; i != arr.length; i++) {
				System.out.print(arr[i] + " ");
			}
			System.out.println();
		}

		public static void main(String[] args) {
			int[] arr = { 6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9 };
			printArray(getMinKNumsByBFPRT(arr, 10));

		}

}