資料結構之約瑟夫環
約瑟夫斯問題（有時也稱為約瑟夫斯置換），是一個出現在電腦科學和數學中的問題。在計算機程式設計的演算法中，類似問題又稱為約瑟夫環。
有
個囚犯站成一個圓圈，準備處決。首先從一個人開始，越過
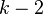個人（因為第一個人已經被越過），並殺掉第k個人。接著，再越過
個人，並殺掉第k個人。這個過程沿著圓圈一直進行，直到最終只剩下一個人留下，這個人就可以繼續活著。
問題是，給定了和
，一開始要站在什麼地方才能避免被處決？
比較簡單的做法是用迴圈單鏈表模擬整個過程，時間複雜度是O(n*m)。程式碼如下：
typedef struct node { int data; struct node *next; } LNode, *LinkList; //構建迴圈連結串列 LinkList Init(int n){ LinkList p,r; LinkList list = NULL; int i; for(i=0;i < n;i++) { p = (LinkList)malloc(sizeof(LNode)); p->data = i+1; p->next = NULL; if(!list) { list = p; } else { r->next = p; } r = p; } p->next = list; return list; } void joseph2(LinkList root,int n,int m){ int flag,i = 1; LinkList pre,p; pre = p = root; flag = 0; while(1){ if(i == m){ pre->next = p->next; printf("%d ",p->data); p = p->next; i=1; } i++; p = p->next; if(++flag > 1) pre = pre->next; if(p == p->next){ printf("%d\n",p->data); break; } } }
第二種解法用到了動態規劃：
無論是用連結串列實現還是用陣列實現都有一個共同點：要模擬整個遊戲過程，不僅程式寫起來比較煩，而且時間複雜度高達O(nm)，當n，m非常大(例如上百萬，上千萬)的時候，幾乎是沒有辦法在短時間內出結果的。我們注意到原問題僅僅是要求出最後的勝利者的序號，而不是要讀者模擬整個過程。因此如果要追求效率，就要打破常規，實施一點數學策略。
為了討論方便，先把問題稍微改變一下，並不影響原意：
問題描述：n個人（編號0~(n-1))，從0開始報數，報到(m-1)的退出，剩下的人繼續從0開始報數。求勝利者的編號。
我們知道第一個人(編號一定是m%n-1) 出列之後，剩下的n-1個人組成了一個新的約瑟夫環（以編號為k=m%n的人開始）:
k k+1 k+2 ... n-2, n-1, 0, 1, 2, ... k-2並且從k開始報0。
現在我們把他們的編號做一下轉換：
k --> 0
k+1 --> 1
k+2 --> 2
...
...
k-2 --> n-2
k-1 --> n-1
變換後就完完全全成為了(n-1)個人報數的子問題，假如我們知道這個子問題的解：例如x是最終的勝利者，那麼根據上面這個表把這個x變回去不剛好就是n個人情況的解嗎？！！變回去的公式很簡單，相信大家都可以推出來：x'=(x+k)%n
這個公式推導是這樣的：
我們把左邊的變數記為x'，右邊的記為x,怎麼把x轉為x'呢，你會發現 (x+k) mod n 就行了。
我們記f(n,k)為還剩n個人時的倖存者編號。很明顯，
n = 1時，f[1,k] = 0;(下標從0開始)
由剛才推出的公式，所以有
f[2,k] = (f[1,k] + k) % 2;
遞推公式
f[1,k]=0;
f[n,k]=(f[n-1,k]+m) % n; (n>1)
有了這個公式，我們要做的就是從1-n順序算出f[i]的數值，最後結果是f[n]。因為實際生活中編號總是從1開始，我們輸出f[n]+1
如果還不能理解，不妨看一個具體的例子
現在假設m=10，k=3
0 1 2 3 4 5 6 7 8 9
第一個人出列後的序列為：
0 1 3 4 5 6 7 8 9
即:
3 4 5 6 7 8 9 0 1（*）
我們把該式轉化為:
0 1 2 3 4 5 6 7 8 (**)
則你會發現: （(**)+3）%10則轉化為(*)式了
也就是說，我們求出9個人中第9次出環的編號，最後進行上面的轉換就能得到10個人第10次出環的編號了 。
由於是逐級遞推，不需要儲存每個f[i]，程式也是異常簡單：
void joseph(int n,int m){
int i, s=0;
for(i=2; i<=n; i++)
s=(s+m)%i;
printf("The winner is %d\n", s+1);
}完整程式碼如下：
#include "stdio.h"
#include "stdlib.h"
typedef struct node {
int data;
struct node *next;
} LNode, *LinkList;
//構建迴圈連結串列
LinkList Init(int n){
LinkList p,r;
LinkList list = NULL;
int i;
for(i=0;i < n;i++) {
p = (LinkList)malloc(sizeof(LNode));
p->data = i+1;
p->next = NULL;
if(!list) {
list = p;
} else {
r->next = p;
}
r = p;
}
p->next = list;
return list;
}
void ListDelNode(LinkList *root,int value){ //因為頭節點可能被刪除，可能改變L儲存的地址，所以傳入L的地址
LinkList list,pre;
int flag = 0; //用於判斷是否是第一次迴圈，用於設定pre的值
list = pre = *root;
while(list){
if(list->data == value){
if(list == pre){
*root = (*root)->next;
printf("刪除掉的值為：%d \n",list->data);
free(list); //free node
break; //break loop
}
pre->next = list->next;
printf("%d ",list->data);
free(list);
break;
}
if(++flag > 1)
pre = pre->next;
list = list->next;
}
}
void printList(LinkList root){
LinkList list = root;
while(list) {
printf("%d ->",list->data);
list = list->next;
}
printf("NULL\n");
}
//總共n個人，每次數m個
void joseph(int n,int m){
int i, s=0;
for(i=2; i<=n; i++)
s=(s+m)%i;
printf("The winner is %d\n", s+1);
}
void joseph2(LinkList root,int n,int m){
int flag,i = 1;
LinkList pre,p;
pre = p = root;
flag = 0;
while(1){
if(i == m){
pre->next = p->next;
printf("%d ",p->data);
p = p->next;
i=1;
}
i++;flag++;
p = p->next;
if(flag > 1)
pre = pre->next;
if(p == p->next){
printf("%d\n",p->data);
break;
}
}
}
int main(){
int n,m;
LinkList L;
printf("N="); scanf("%d", &n);
printf("M="); scanf("%d", &m);
L = Init(n);
joseph2(L,n,m);
joseph(n,m);
//ListDelNode(&L,3);
//printList(L);
}Ref：