在第一篇打分系統漫談1 - 時間衰減我們聊了兩種相對簡單的打分算法Hacker News和Reddit Hot Formula，也提出了幾個這兩種算法可能存在的問題，這一篇我們就其中的兩一個問題進一步討論：

• 如何綜合瀏覽量和點贊量對文章進行打分[期望效用函數->點贊率]
• 如何解決瀏覽量較小時，點贊率不置信的問題[wald Interval -> wilson]

Reddit Hot Formula？ 期望效用函數！

讓我們從上一篇我們提到的Reddit Hot Formula來說起，拋開文章質量的懲罰項，只考慮點贊拍磚的低配版打分公式是
\[ score = sign(U-D)* log_{10}{|U-D|} + seconds/4500 \]

• 用戶刷新界面的行為$ \sim Poisson(\lambda)$
• 每次刷新看到新/老文章的概率是\(q/(1-q)\), 喜歡/不喜歡的概率是\(p/(1-p)\)
• 老文章效用為0，喜歡的新文章效用為1， 不喜歡的新文章效用為-1

上述概率p,q可以用已有數據進行估計：

在沒有任何和文章相關的信息時，喜歡不喜歡的概率是一樣的\(p=\frac{1}{2}\), 當我們獲得一篇文章的點贊量和拍磚數時我們可以用點贊率對概率進行更新得到\(p = \frac{U+1}{U+D+2}\)

概率q是一篇t時刻前發布的文章沒有被作者讀過的概率,換言之就是用戶在t時間內沒有刷新界面的概率\(q = p(N_\lambda=0)= p(x>t)= exp(-\lambda t)\)

綜上我們可以得到對數效用的表達式：

\[ \begin{align} Utility & = p * q -(1-p) * q \\ & = exp(-\lambda t ) *(\frac{U+1}{U+D+2} - \frac{D+1}{U+D+2}) \ &= exp(-\lambda t ) *(\frac{U-D}{U+D+2}) \ log(Utility ) & = log(U-D) - log(U+D+2) - \lambda t \\end{align} \]

和上述Reddit Hot Formula對比我們會發現當U>D的時候，兩個表達式是基本一致的，最大的不同是Reddit沒有期望效用的第二個對數項\(log(U+D+2)\)

我們舉個例子你就會明白這種打分可能存在的問題，我們拿Stack overflow來舉個例子，下圖的兩個問題獲得了差不多的投票57 vs. 53，但是會發現第一個問題比第二個問題多一倍的瀏覽量4k vs. 2K, 所以從投票率來看反而是第二個問題的投票率更高。

點估計？區間估計！

這樣看似乎我們應該使用點贊（投票）率而非簡單的點贊量來對文章進行打分，但是點贊率真的永遠可信麽？ 我們再看一個例子

單從投票率來看，第一個問題投票率高達50%但是瀏覽量只有2 ，而第二個問題投票率較低但是瀏覽量很高。如果但從投票率來看，似乎第一個問題排名更高，但是直覺告訴我們第二個問題應該排名更靠前。這就涉及統計學中點估計的置信度問題。

讓我們來把用戶點贊這個行為抽象一下，我們假設每一個用戶要麽點贊要麽拍磚，每一個用戶之間的行為之間獨立，所以每個用戶\(\sim Bernoulli(p)\), 其中p是點贊的概率。當樣本量足夠大的時候，根據大數定律用戶點贊的頻率會趨於點贊率$\lim\limits_{x \to \infty} P(|\frac{n_x}{n} - p| < \epsilon)=1 $

但是當用戶量不夠，樣本比較小的時候，計算的點贊率會和總體概率會存在較大的偏差。一種解決方法就是使用區間估計而非點估計，我們給出點贊率估計的下邊界而非點贊率的估計值。

最常用的二項分布的區間估計由近似正態分布給出。根據大數定律，參數為n,p的二項分布在\(n \to \infty\)的時候 \(\frac{\hat{p}-p}{\sqrt{p(1-p)/n}} \sim N(0,1)\)。根據正態分布的置信區間我們會得到二項分布的近似區間估計如下
\[ \begin{align} & p( | \frac{\hat{p}-p}{\sqrt{p(1-p)/n}} | < z_{\alpha/2}) = 1- \alpha \\ & where \, 置信度是0.95，\alpha = 0.05 \&\hat{p}是根據每個用戶點贊行為給出的點贊率的估計\&n是樣本量，可以是用戶點贊+拍磚的總和，或者是用戶瀏覽量\&p是總體的點贊率是我們希望得到的估計\\end{align} \]

Wald Interval 對上述近似區間用樣本估計\(\hat{p}\)替代總體p，給出了最常用的二項分布置信區間：
\[ \begin{align} p_-,p_+ = \hat{p} \pm z_{\alpha/2}\sqrt{\hat{p}(1-\hat{p})/n} \end{align} \]
wald置信區間適用大多數情況，但是在下面三個情況下會存在問題：

• 樣本不夠，n太小時，\(\hat{p}\)和總體的p相比會偏差較大
• \(p \to 0\) or \(p \to 1\)會導致方差趨於0，使得置信區間顯著偏窄
• \(p =0，1\) 置信區間長度為0

而在估計文章點贊率這個場景下我們不可避免的會碰到上述3個情況，在這種情況我們往往會使用更加復雜的置信區間算法。來來來下面讓我們說說其中一種高配版的置信區間- Wilson Interval

Wilson Score

Wilson對Walt置信區間做了修正, Wilson置信區間的上下界如下：
\[ \begin{align} p_-,p_+ = \frac{\hat{p} + \frac{z^2_{\alpha/2}}{2n}} {1 +\frac{z^2_{\alpha/2}}{n}} \pm z_{\alpha/2}\frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z^2_{\alpha/2}}{4n^2} }}{1 +\frac{z^2_{\alpha/2}}{n}} \end{align} \]

看著老復雜了，讓我們來拆解一下你就會發現原理蠻好理解的。先說說對總體均值的估計，wilson對\(\hat{p}\)進行了如下調整：

\[ \begin{align} \hat{p} \to \tilde{p} = \frac{\hat{p} + \frac{z^2_{\alpha/2}}{2n}} {1 +\frac{z^2_{\alpha/2}}{n}} \begin{align} \]
當樣本量足夠大Wilson和Walt對總體均值的估計會趨於一致。當樣本量很小的時候, 不同於walt,wilson給樣本估計加了一個\(\frac{1}{2}\)的貝葉斯前置概率(點贊和拍磚的概率各是50%),然後不斷用新增樣本來對這個前置概率進行調整。從而避免樣本較小的時候樣本估計過度偏離總體的問題。
\[ \begin{align} when \lim\limits_{n \to \infty} \tilde{p} \to \hat{p} \when \lim\limits_{n \to 0} \tilde{p} \to \frac{1}{2} \\end{align} \]
方差部分也做了相同的處理, 當樣本足夠大的時候wilson和walt對總體方差的估計會趨於一致，但是當樣本小的時候和上述樣本均值的處理方法一樣，會趨於貝葉斯前置概率對應的方差\(\hat{p} \to \frac{1}{2} \Rightarrow \hat{p}(1-\hat{p}) \to \frac{1}{4}\)
\[ \begin{align} \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \to \frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z^2_{\alpha/2}}{4n^2} }}{1 +\frac{z^2_{\alpha/2}}{n}} \end{align} \]
下面兩張圖片很直觀的給出了不同樣本數量(n=10 vs.100)下，樣本均值的估計所對應的置信區間的長度（方差估計）。當樣本大的時候Wilson和Wald幾乎一樣，當樣本小的時候，隨著p趨於0 or 1,Wilson置信區間會顯著寬於Walt區間。

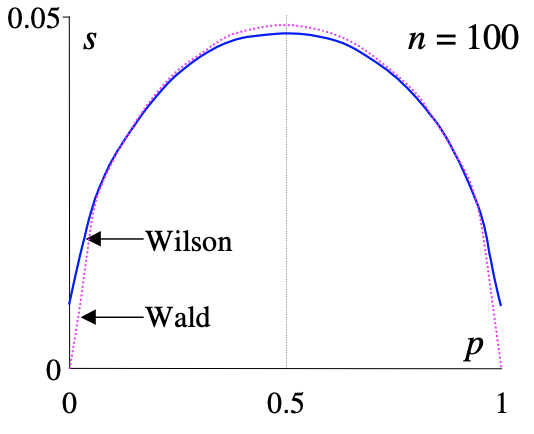
而Wilson打分就是取Wilson置信區間的下界:
\[ \begin{align} score= \frac{\hat{p} + \frac{z^2_{\alpha/2}}{2n}} {1 +\frac{z^2_{\alpha/2}}{n}} - z_{\alpha/2} \frac{\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z^2_{\alpha/2}}{4n^2} }}{1 +\frac{z^2_{\alpha/2}}{n}} \end{align} \]

Wilson打分方式有幾個很好的特性：

• 點贊率(p)一樣，瀏覽量(n)越高得分越高
• 點贊率趨於0時, score = 0
• 點贊率趨於1時, score = \(\frac{1}{1+z^2_{\alpha/2}/n}\), 瀏覽量越高，得分越接近1，反之瀏覽量越小，得分越低，這樣會對小樣本點贊率高的問題進行調整
• 置信度越高，\(z_{\alpha/2}\)越大，點贊率越不重要，而樣本量n越重要

在下一篇文章我們繼續聊聊另一種更靈活的處理小樣本打分的方法- 貝葉斯更新

Reference

1. https://www.ucl.ac.uk/english-usage/staff/sean/resources/binomialpoisson.pdf
2. http://www.ruanyifeng.com/blog/2012/03/ranking_algorithm_wilson_score_interval.html
3. http://www.evanmiller.org/how-not-to-sort-by-average-rating.html
4. 二項分布參數的區間估計,朱永生《粒子物理數據分析基礎與前沿》研討會

打分排序系統漫談2 - 點贊量？點贊率?! 置信區間！