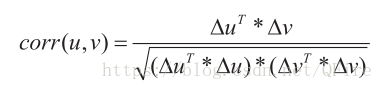Python預測分析(1):關於預測的兩類核心演算法
本書涉及的機器學習問題通常是指“函式逼近”問題。是有監督學習問題的一個子集。線性迴歸和邏輯迴歸是解決此類函式逼近問題最常見的演算法。函式逼近問題包含了各種領域中的分類問題和迴歸問題,如文字分類、搜尋響應、廣告放置、垃圾郵件過濾、使用者行為預測、診斷等。從廣義上說,本書涵蓋了解決函式逼近問題的兩類演算法:懲罰線性迴歸和整合方法。
為什麼這兩類演算法如此有用?
1.“An Empirical Comparison of Supervised Learning Algorithms,” Rich Caruana, Alexandru Niculescu-Mizi
本書涵蓋的演算法提升決策樹(Boosted Decision Trees)、隨機森林(Random Forests)、投票決策樹(Bagged Decision Trees)和邏輯迴歸(Logistic Regression)
2.“An Empirical Evaluation of Supervised Learning in High Dimensions,” Rich Caruana,Nikos Karampatziakis 和 Ainur Yessenalina
懲罰迴歸方法是由普通最小二乘法(OLS)衍生出來的。OLS的一個根本問題就是有時它會過擬合。懲罰線性迴歸可以減少自由度使之與資料規模、問題的複雜度相匹配。對於具有大量自由度的問題,懲罰線性迴歸方法獲得了廣泛的應用。(統計學上的自由度是指當以樣本的統計量來估計總體的引數時,樣本中獨立或能自由變化的自變數的個數稱為該統計量的自由度),基因問題,通常其自由度(基因的數目)是數以萬計的;文字分類問題,其自由度可以超過百萬。
整合方法的基本思想是構建多個不同的預測模型,然後將其輸出做某種組合作為最終的輸出,如平均值或採用多數人的意見。單個預測模型叫作基學習器(base learners)。計算學習理論(computation learning theory)的研究結果證明只要基學習器比隨機猜測稍微好些,那麼整合方法就可以達到相當好的效果。
2、通過理解資料來了解問題
屬性和標籤的不同型別決定模型的選擇,主要原因是很多機器學習演算法只能處理數值變數,不能處理類別變數或因素變數。例如,懲罰迴歸演算法只能處理數值變數,SVM、核方法、KNN也是同樣。
當標籤是數值的,就叫作迴歸問題。當標籤是類別的,就叫作分類問題。一個分類器就相當於只算出一個等高線,而不再考慮與這條分界線的遠近距離之類的問題,而回歸的方法就相當於要繪製一個完整的地形圖。
新資料集的注意事項:
- 行數、列數、規模
- 類別變數的數目、類別的取值範圍
- 缺失的值
- 屬性和標籤的統計特性
2.2、分類問題:用聲納發現未爆炸的水雷
資料集來自UC Irvine資料倉庫:測試聲納是否可以用於檢測在港口軍事行動後遺留下來的未爆炸的水雷。
資料集的物理特性rockVminesSummaries.py
__author__ = 'mike_bowles'
import urllib2
import sys
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-databases/undocumented/connectionist-bench/sonar/sonar.all-data")
data = urllib2.urlopen(target_url)
xList = []
labels = []
for line in data:
row = line.strip().split(",")
xList.append(row)
sys.stdout.write("Number of Rows of Data = " + str(len(xList)) + '\n')
sys.stdout.write("Number of Columns of Data = " + str(len(xList[1])))Number of Rows of Data = 208
Number of Columns of Data = 61如果資料集規模增加到1000x1000,懲罰線性迴歸訓練時間將不到一分鐘,而整合方法訓練時間需要幾分鐘。萬級規模,則懲罰線性迴歸的訓練時間將達到3~4小時,而整合方法則長達12~24小時。
確定每個屬性的特徵
第一步計算此屬性的均值和方差,可以加強直觀感受
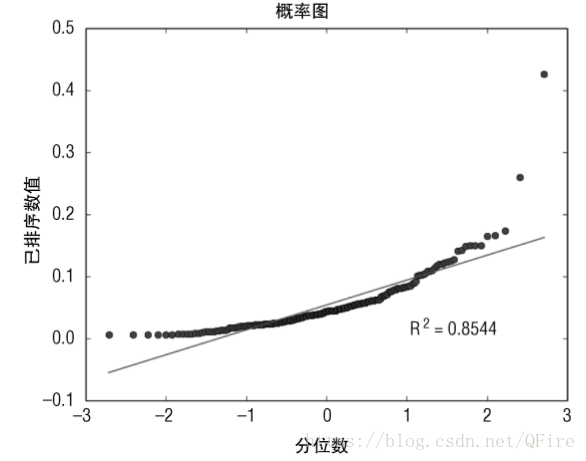
第二步找到異常值,一種方法是:將一組數字按照百分位數進行劃分。例如,第25百分位數是含有最小的25%的數,第50百分位數是含有最小的50%的數。把這種分組視覺化最簡單的方法是假想把這些資料按順序排列。使用Python的probplot函式來幫助確認資料中是否含有異常點。分佈圖展示了資料的百分位邊界與高斯分佈的同樣百分位的邊界對比。如果此資料服從高斯分佈,則畫出來的點應該是一條直線。
Pandas工具包可以幫助自動化資料統計分析的過程,已經被證實在資料預處理階段特別有用。Pandas工具包可以將資料讀入一種特定的資料結構,叫作資料框(data frame),其是依據CRAN-R資料結構建模的。可以把資料框當成一個表格或者類似矩陣的資料結構。Pandas可以自動計算出均值、方差、分位樹。
視覺化展示:
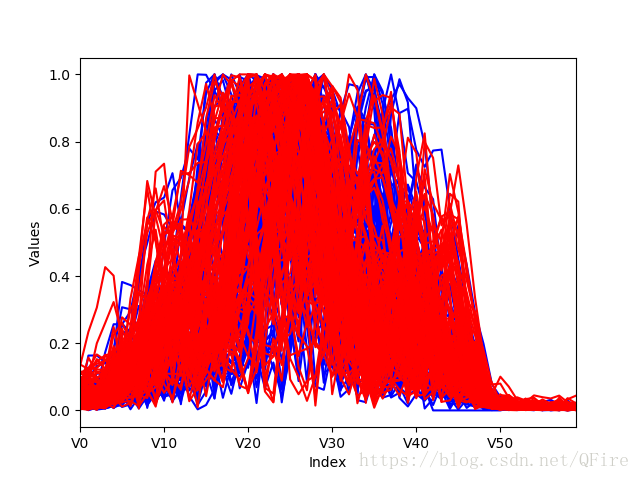
對於具有多個屬性問題的一種視覺化方法叫作平行座標圖
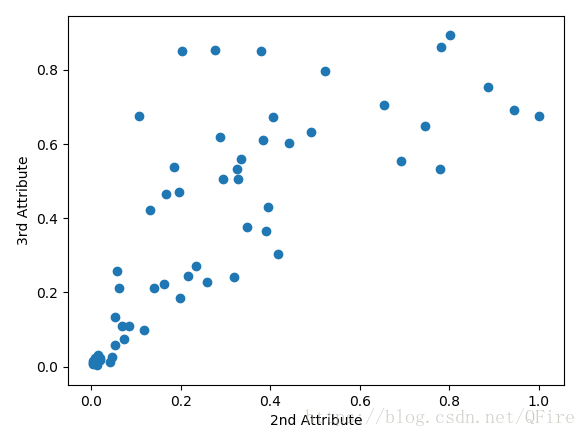
瞭解屬性之間的關係可以繪製屬性與標籤的交會圖 (又叫作散點圖)展示了這些屬性對之間關係的密切程度。基本上,如果散點圖上的點沿著一條“瘦"直線排列,則說明這兩個變數強相關;如果這些點形成一個球型,則說明這些點不相關。
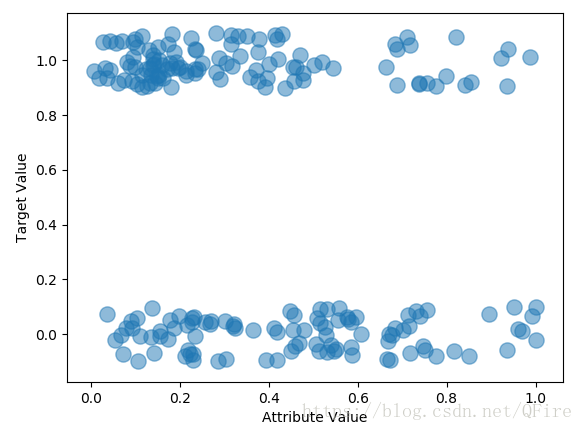
第35屬性與標籤的關係
兩個屬性的相關程度可以由皮爾遜相關係數來量化
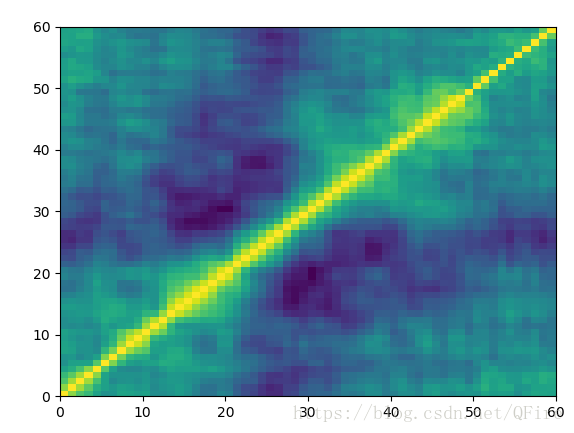
用熱圖(heat map)展示屬性和標籤的相關性
如果問題有100以上的屬性,則很難把散點圖壓縮到一頁。獲得大量屬性之間相關性的一種方法是計算出每對屬性的皮爾森相關係數後,將相關係數構成一個矩陣,然後把這些矩陣元素畫到熱圖上。沿著斜對角線的淺色區域證明索引值相近的屬性相關性較高。
# -*- coding: utf-8 -*-
__author__ = 'mike_bowles'
import urllib2
import sys
target_url = ("https://archive.ics.uci.edu/ml/machine-learning-databases/undocumented/connectionist-bench/sonar/sonar.all-data")
data = urllib2.urlopen(target_url)
xList = []
labels = []
for line in data:
row = line.strip().split(",")
xList.append(row)
# 資料行列數
nrow = len(xList)
ncol = len(xList[1])
# 資料的屬性,是數值還是類別型
type = [0]*3
colCounts = []
for col in range(ncol):
for row in xList:
try:
a = float(row[col])
if isinstance(a, float):
type[0] += 1
except ValueError:
if len(row[col]) > 0:
type[1] += 1
else:
type[2] += 1
colCounts.append(type)
type = [0]*3
sys.stdout.write("Col#" + '\t' + "Number" + '\t' + "Strings" + '\t ' + "Other\n")
iCol = 0
for types in colCounts:
sys.stdout.write(str(iCol) + '\t\t' + str(types[0]) + '\t\t' + str(types[1]) + '\t\t' + str(types[2]) + "\n")
iCol += 1
# 獲取數值型屬性的描述性統計資訊和類別型屬性具體型別的數量分佈
import numpy as np
type = [0]*3
colCounts = []
col = 3
colData = []
for row in xList:
colData.append(float(row[col]))
colArray = np.array(colData)
colMean = np.mean(colArray)
colsd = np.std(colArray)
sys.stdout.write("Mean = " + '\t' + str(colMean) + '\t\t' + "Standard Deviation = " + '\t' + str(colsd) + "\n")
# calculate quantile boundaries
ntiles = 4
percentBdry = []
for i in range(ntiles+1):
percentBdry.append(np.percentile(colArray, i*(100)/ntiles))
sys.stdout.write("\nBoundaries for 4 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
ntiles = 10
percentBdry = []
for i in range(ntiles+1):
percentBdry.append(np.percentile(colArray, i*(100)/ntiles))
sys.stdout.write("\nBoundaries for 10 Equal Percentiles \n")
print(percentBdry)
sys.stdout.write(" \n")
#The last column contains categorical variables
col = 60
colData = []
for row in xList:
colData.append(row[col])
unique = set(colData)
sys.stdout.write("Unique Label Values \n")
print(unique)
# count up the number of elements having each value
catDict = dict(zip(list(unique), range(len(unique))))
catCount = [0]*2
for elt in colData:
catCount[catDict[elt]] += 1
sys.stdout.write("\nCounts for Each Value of Categorical Label \n")
print(list(unique))
print(catCount)
# 分點陣圖
import pylab
import scipy.stats as stats
col = 3
colData = []
for row in xList:
colData.append(float(row[col]))
#stats.probplot(colData, dist="norm", plot=pylab)
#pylab.show()
# 用Pandas讀入資料、分析資料
import pandas as pd
from pandas import DataFrame
import matplotlib.pyplot as plot
rocksVMines = pd.read_csv(target_url, header=None, prefix="V")
print(rocksVMines.head())
print(rocksVMines.tail())
# print summary of data frame
summary = rocksVMines.describe()
print(summary)
'''
# 平行座標圖
for i in range(208):
if rocksVMines.iat[i, 60] == "M":
pcolor = "red"
else:
pcolor = "blue"
# plot rows of data as if they were series data
dataRow = rocksVMines.iloc[i, 0:60]
dataRow.plot(color=pcolor)
plot.xlabel("Index")
plot.ylabel("Values")
plot.show()
'''
# 交會圖
dataRow2 = rocksVMines.iloc[1, 0:60]
dataRow3 = rocksVMines.iloc[2, 0:60]
plot.scatter(dataRow2, dataRow3)
plot.xlabel("2nd Attribute")
plot.ylabel("3rd Attribute")
plot.show()
dataRow21 = rocksVMines.iloc[20, 0:60]
plot.scatter(dataRow2, dataRow21)
plot.xlabel("2nd Attribute")
plot.ylabel("21st Attribute")
plot.show()
# 第35屬性
target = []
for i in range(208):
if rocksVMines.iat[i, 60] == "M":
target.append(1.0)
else:
target.append(0.0)
dataRow = rocksVMines.iloc[0:208, 35]
plot.scatter(dataRow, target)
plot.xlabel("Attribute Value")
plot.ylabel("Target Value")
plot.show()
from random import uniform
target = []
for i in range(208):
if rocksVMines.iat[i, 60] == "M":
target.append(1.0 + uniform(-0.1, 0.1))
else:
target.append(0.0 + uniform(-0.1, 0.1))
dataRow = rocksVMines.iloc[0:208, 35]
plot.scatter(dataRow, target, alpha=0.5, s=120)
plot.xlabel("Attribute Value")
plot.ylabel("Target Value")
plot.show()
# 熱圖
corMat = DataFrame(rocksVMines.corr())
plot.pcolor(corMat)
plot.show()2.4、基於因素變數的實數值預測:鮑魚的年齡
鮑魚資料集的問題是根據某些測量值
2.5 用實數值屬性預測實數值目標:評估紅酒口感
每一種紅酒都有一系列化學成分的測量指標,包括酒精含量、揮發性酸、亞硝酸鹽。每種紅酒都有一個口感評分值,是三個專業評酒員的評分的平均值。問題是構建一個預測模型,輸入化學成分的測量值,預測口感評分值,使之與評酒員的評分一致。
2.6 多類別分類問題:它屬於哪種玻璃
多分類問題