冒泡、歸併和快速排序
- 氣泡排序
- 歸併排序
- 快速排序
氣泡排序
這應該是初學者最熟悉的排序,就是
相鄰兩數比較,若逆序則交換。n - 1 趟之後陣列有序。
執行的過程上看,就像一個大泡泡逐漸浮出水面。
冒泡的時間複雜度
最好境況下,陣列正序,比較一趟 ,
最壞情況下,陣列逆序,比較
時間複雜度
平均情況下也是
歸併排序
使用分治法的一種異地排序。
原理如下
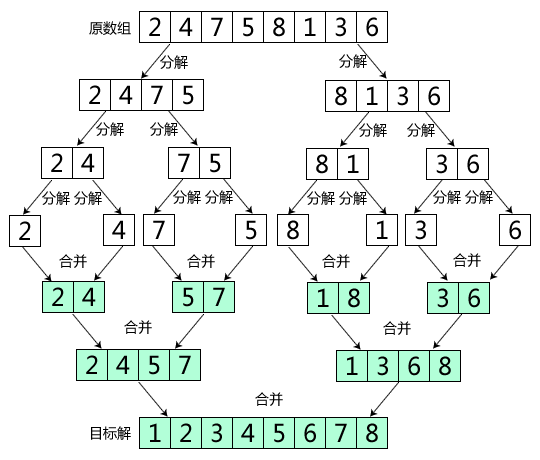
將一個大陣列,分解成兩個子陣列,分別排序,在合併兩個有序陣列。
遞迴進行,直到陣列長度為1
如圖
歸併的時間複雜度
遞迴的時間複雜分析
1)分解 直接分解, 時間為常數級
2)治之 對兩個陣列排序, 時間為
3)合併 掃描一遍陣列,時間為線性級
整體的時間為
由遞迴表示式得
分析一下可以得出,正序或逆序對歸併排序的影響並不大,不管是否有序,他都會走完全程,可能在合併的時候有一點優勢,但時間複雜度仍然沒變。
我的程式碼如下
public static void sort(int[] data, int p, int r){
if(p < r){
int q = (p+r) / 2;
sort(data,p,q);
sort(data,q+1 快速排序
分析氣泡排序,每一趟都要和 n - i 個數比較,而歸併排序,將陣列分成兩部分,就可以減少比較,
那如果每一趟不是找到最大的“泡泡”,而是到一箇中間的位置,(分界點)
而將陣列分成兩部分,一邊都比這個“泡泡”小,一邊比這個“泡泡”大,然後遞迴下去,也能達到有序。
這就是快速排序的思想。我的程式碼
public void sort(int[] data,int p, int r){
int q;
if(p < r){
q = partition(data,p,r); // 分解過程
sort(data,p,q-1);
sort(data,q+1,r);
}
}與歸併的不同
歸併和快速都採用了分治法,將陣列分成兩部分,分別排序而兩者有什麼不同呢
從程式碼就可以看出
歸併排序 是先遞迴後合併 分解不需成本 (先享受後付出代價)
快速排序 是先分解後遞迴 合併不需成本 (先付出後收穫成果)
分解過程
分解過程我瞭解了三個版本。
第一種快速排序的分解過程 (分界點為第一個元素)
陣列 A 排序第 p 到 r 個元素
選擇一個分界點“泡泡”(這裡選擇第一個元素), 其值記為 x
設定兩個遊標 i =p,j = p+1
進入迴圈 若A[j] <= x , i ++ , 交換 A[i] <=>A[j]
否則 j ++, 直到 j = r
最後交換 A[p] <=>A[i]
圖解:
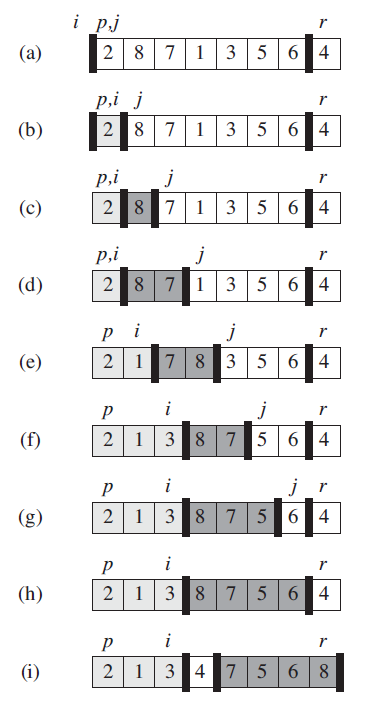
第二種快速排序的分解過程 (分界點為最後一個元素)
陣列 A 排序第 p 到 r 個元素
選擇一個分界點“泡泡”(這裡選擇最後一個元素), 其值記為 x
設定兩個遊標 i =p-1,j = p
進入迴圈 若A[j] <= x , i ++ , 交換 A[i] <=>A[j]
否則 j ++, 直到 j = r
最後交換 A[r] <=>A[i+1]
圖解:
這兩種方法大同小異,迴圈過程一樣,就是兩個遊標的初值,和迴圈的終止條件差一個位置
我的程式碼
public static int partition(int[] data,int p, int r){
int x = data[r];
int i = p-1;
int temp = 0;
for(int j = p; j < r; j ++){
if(data[j] <= x){
i = i + 1;
temp = data[i];
data[i] = data[j];
data[j] = temp;
}
}
temp = data[i+1];
data[i+1] = data[r];
data[r] = temp;
return i + 1;
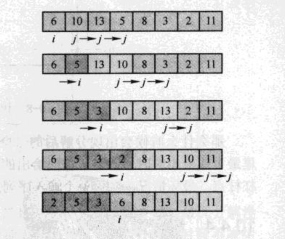
}第三種快速排序的分解過程 (從兩邊向中間)
陣列 A 排序第 p 到 r 個元素
選擇一個分界點“泡泡”(這裡選擇第一個元素), 其值記為 pivotkey
設定兩個遊標 i =p,j = r
進入迴圈
先從後向前掃描 (j–) ,直到 A[j] < pivotkey , 令 A[i] =A[j]
再從後向前掃描(i++),直到 A[i] > pivotkey , 令A[i] =A[j]
當 i >= j 時迴圈結束
最後交換 A[i] =pivotkey
在此過程中不用交換 A[i] 、 A[j] ,因為 A[i] 、 A[j]中的一個值是分界點,而分界點的值已被記錄 (pivotkey),所以不需要再陣列中多餘復值,最後一步到位就可以了。而上面兩個過程並沒有這個特點。
圖解:
我的程式碼
public static int partition2(int[] data,int p, int r){
int x = data[p];
int i = p;
int j = r;
while(i < j){
while(i<j && data[j] >= x) j --;
data[i] = data[j];
while(i<j && data[i] <= x) i ++;
data[j] = data[i];
}
data[i] = x;
return i;
}效率測試
我用一百萬條資料在java上的檢測表明
前兩種方法的平均時間為 115 毫秒
第三種方法的平均時間為 130 毫秒
我也覺得很奇怪,理論上第三種方法減少了很多賦值操作為什麼還會慢呢。
進一步的測試
三種方法的data 與 x 的比較次數差不多。
第三種方法比前兩種的 逆序情況少 (即方法一需要交換,方法三需要賦值)(一百萬條資料時平均少了 2000000 次)。
這個結果更加是我奇怪,逆序情況少說明演算法更優呀!
分析一下程式
第三種方法中有迴圈的巢狀,而且比較 i < j 的次數多了很多。(一百萬條資料時平均多了 5000000 次)。
只能說演算法是好的,但實現的時候並不一定是好的。可能這個問題還有關記憶體的查詢,快取的命中等等。
時間複雜度
和歸併排序中有序或無序對時間沒有太大影響,那對快速排序呢。
設想當陣列有序(無論正序逆序),我們每次選出的“分界線”(第一或最後的元素)就是最大或最小的,這樣就不能將陣列分成兩部分,那這個“分界線”其實就是氣泡排序中最大的“泡泡”。
當陣列有序時,快速排序退化成氣泡排序,就是最壞情況
(而且由於是遞迴效率效果很差,在10萬條資料時我的JVN直接“記憶體溢位”,因為遞迴太深)
那最好情況是什麼呢,就是我們想讓
選出的“分界線”能剛好平分陣列
好的結論就是
最壞的時間複雜度:
平均的時間複雜度:
改進(隨機化)
由上面的分析,“分界點”的選擇會影響演算法的時間。那為了避免最壞情況的發生,或者說避免敵人(黑客知道了你的演算法你就完了)的攻擊,我們在選擇“分界點”時要進行隨機化,除非你的運氣太差,每次隨機到最值,不然效率就是好的。
文獻參考
[1] 嚴蔚敏,吳偉民 . 資料結構(C語言版)
[2] 鄒恆明. 演算法之道
[3] 演算法導論