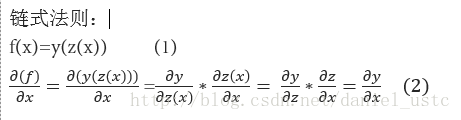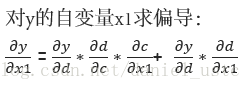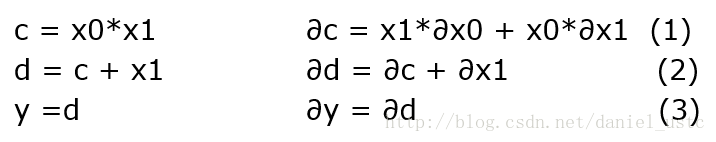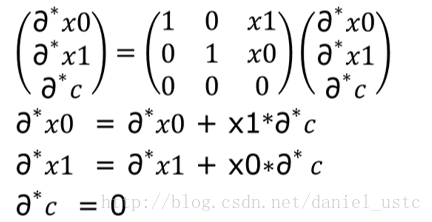0. 緣由

下面介紹下為什麼要引入自動 自動微分(automatic differentiation -> AD )。

• 一個優化問題的例子
  假設現在我們在解決一個機器學習的問題，有了一些訓練樣本，現在需要尋找一個最優的函式，使得函式對輸入X的估計Y’與實際輸出Y之間的期望風險最小化。利用已知的經驗資料（訓練樣本）來計算得到的誤差，被稱之為經驗風險。使用對引數求經驗風險來逐漸逼近理想的期望風險的最小值，就是我們常說的經驗風險最小化（Empirical risk minimization，ERM）原則。我們利用經驗風險最小化的原則求解機器學習的步驟為：
• 定義一個模型，這個模型有一定的引數，其能夠在給定輸入後根據模型預測輸出；
• 定義一個損失函式(loss function)，這個損失函式能夠計算出真實值和模型預測值的誤差，比如 平方損失、對數損失、0-1損失等等（損失函式儘量 是一個凸函式，便於收斂計算）；
• 獲得一些訓練資料；
• 在訓練資料上利用ERM原則對模型引數進行擬合，為防止過度擬合的模型出現（過於複雜的模型），在損失函式裡增加一個每個特徵的懲罰因子，即加入正則化項。

上面所述的在訓練資料上結合ERM原則對模型引數進行擬合的過程其實就是一個機器學習的過程。機器學習的目標就是最小化我們的損失函式，當各個引數學到一定程度後，我們的損失函式也收斂，即達到最小值，這個學習的過程需要以下步驟：

• 寫出在訓練資料上關於模型引數的損失函式；
• 對損失函式求解關於不同模型引數的偏導；
• 寫程式碼求解導數；
• 基於損失函式的引數學習演算法現存的演算法比較多:SGD,LBFGS,AdaGrad…；

上面求解方法存在的問題：

• 在相關函式的引數求導以及寫出求導程式碼花費很多精力;
• 自己推導偏導及寫程式碼求導，往往一步不慎，全盤皆輸（這樣做很容易出錯）；
• 我們不必什麼都要親力親為，應該把更多精力放在新的模型和實驗上；

幾種微分求解的方法

根據這篇paper：Automatic differentiation in machine learning: a survey中的介紹,目前微分求解有如下的方法：

• 手動求解法(Manual Differentiation)
• 數值微分法(Numerical Differentiation)
• 符號微分法(Symbolic Differentiation)
• 自動微分法(Automatic Differentiation)

下面說下各自的優缺點：
1. 手動求導效率低下、易於出錯。
2. 數值微分：根據導數定義有：

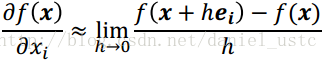
數值微分易於實現，但引數多時計算量較大，且引起的round off error(舍入錯誤)和truncation error(截斷錯誤), 使用center difference(中心差分)可以減少truncation error但是，存在rouding error, 往往我們利用Numerical Differentiation來檢驗其它微分演算法的正確性，如在BP計算的時候，gradient check就是利用數值微分法進行check point。
center difference：

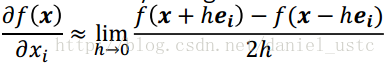
3.符號微分是為了解決手動微分以及數值微分的缺點而提出來的，其利用代數軟體，實現微分的一些公式，它試圖將問題轉化為一個純數學符號問題。符號微分的缺點是它經常導致複雜、晦澀難懂的表示式，最終出現“表示式膨脹”（expression swell）問題，它使得問題符號微分求解的表示式急速“膨脹”，導致最終求解速度變慢。
4.自動微分利用鏈式法則達到自動求導的效果。

自動微分法是一種介於符號微分和數值微分的方法：數值微分強調一開始直接代入數值近似求解；符號微分強調直接對代數進行求解，最後才代入問題數值；自動微分將符號微分法應用於最基本的運算元，比如常數，冪函式，指數函式，對數函式，三角函式等，然後代入數值，保留中間結果，最後再應用於整個函式。因此它應用相當靈活，可以做到完全向使用者隱藏微分求解過程，由於它只對基本函式或常數運用符號微分法則，所以它可以靈活結合程式語言的迴圈結構，條件結構等，使用自動微分和不使用自動微分對程式碼總體改動非常小，並且由於它的計算實際是一種圖計算，可以對其做很多優化，這也是為什麼該方法在現代深度學習系統中得以廣泛應用。

1. Automatic differentiation (AD)

在數學和計算代數領域，automatic differentiation (AD)又稱為 algorithmic differentiation 或者 computational differentiation。AD是一個可以對程式程式碼表示的數學函式進行自動微分的技術。AD利用鏈式法則來達到自動求解的目錄，AD有兩種主要的方法：

1. 程式碼轉換（source-code transformation）（R. Giering and T. Kaminski. 1998）：
   
   • 利用一個程式碼轉換編譯器，這個編譯器會分析原始碼，然後產生一個和原始碼對應的伴隨模式(adjoint model)程式，編譯時的程式碼生成（如用 flex-bison 做詞法、語法分析）；
   • 優點是靜態生成效率高(原始演算法的3~4倍) ;
   • 一次生成，多次使用，缺點是學習門檻較高（編譯原理…）；
   • 很多比較好的工具非免費；
   • 對現代程式語言特性的限制（如C++類、模板等）；
2. 運算子過載(operator overloading)
   
   • 應用比較廣泛，很多程式語言特性可以很好的工作；
   • 優點是簡單直接，缺點是動態生成成本較高（代表性的工具效率是原始演算法的10~35倍）。
   • 較多免費開源 C++ 工具 (e.g. ADOL-C, CppAD, Sacado)；

AD 這兩種實現方式：運算子過載與程式碼生成，兩種方式的原理都一樣，鏈式法則。AD相關工具，請到這個http://www.autodiff.org/頁面。自動微分（AD）是計算導數的最優方法，比符號計算、有限微分更快更精確，AD已經廣泛應用在優化領域，包括人工神經網路的訓練演算法 back-propagation（BP）等。

2. AD基本原理

不難想象，任何計算都可以由第1步到第k步的序列形式，其中第 i 步計算的輸入，在之前的 i-1 步中已經計算（例如編譯器生成的彙編指令序列）。因此，任何計算都可以看作形式如子計算序列的複合函式，結合微積分中的鏈式法則AD有forward-mode 和reverse mode兩種計算方式。下面結合實際的例子進行說明：

• 計算圖

假設有算術計算公式：

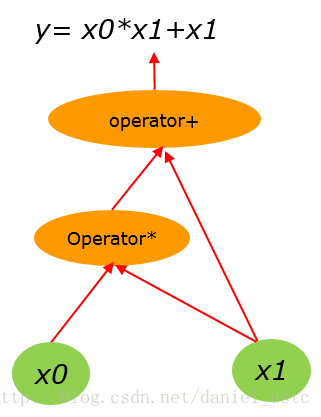
y= x0*x1 + x1 （1）

(1)式用計算圖表示為：

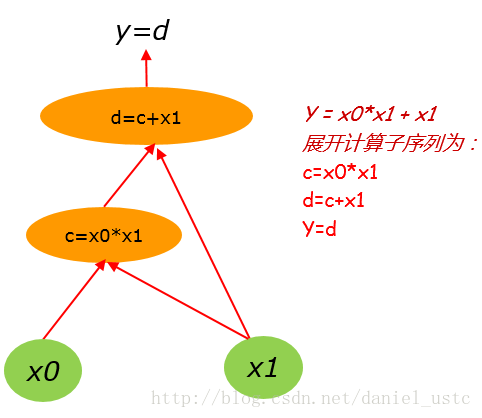
把(1)式展開計運算元序列為：

c=x0*x1     
d=c+x1      
y=d         

對應的計算圖為：

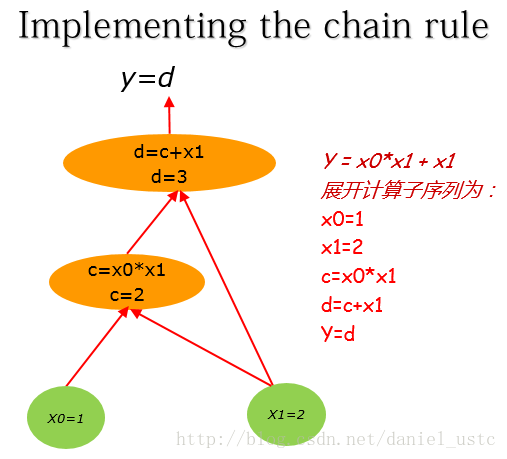
這裡假設x0,x1的初值分別為：1, 2。 把(1)式展開計運算元序列為：

x0=1        
x1=2          
c=x0*x1     
d=c+x1      
y=d         

對應計算圖為：

• 計算圖上的導數求解
  理解計算圖上的導數求解的關鍵是要理解：邊上的導數。x0直接影響到c,如果x0改變，那麼c會發生什麼變化？對於這種情形我們稱它為c關x0的偏導數。

為了計算計算圖上的偏導數，我們需知道導數的加法和乘法原則：

利用上面兩個原則結合計算圖，其中圖中的邊即為偏導數則有：

有了上面的計算圖，為了求偏導dy/dx0, 我們還需知道鏈式法則, 簡單概括起來即為：“由兩個函式湊起來的複合函式，其導數等於裡邊函式代入外邊函式的導數（注意，裡面的函式看成一個自變量了），乘以裡邊函式的導數”，數學表示式即為：

因此結合導數的加法和乘法原則以及鏈式法則，可知對於特點節點的偏導數及法則是：
一個節點對另一個節點求偏導，對從這個節點到另個所有路徑進行累加，其中每條路徑上的值是這條路徑所有邊進行累積。舉個例子比如y對x1求偏導：

利用上述公式結合x0=1，x1=2的初始值可知，dy/dx1= 1*1*1+1*1 = 2 ,符合實際結果。

• forward-mode 和 reverse-mode

微分流形上的向量有兩種：切空間 (Tangent space)的向量和對偶空間 (Dual space)的向量。
其中切空間的基{∂∂xi}是關於座標系的偏導,對偶空間的基是關於座標系的微分{dxi}。從切矢量出發可以得到自動微分的正序模式 (forward mode, tangent-linear)，從對偶矢量出發可以得到自動微分的逆序模式 (reverse mode，adjoint mode,backward mode)。

1. forward-mode
任意切向量 dds=dxids∂∂xi 的定義是其對應的方向導數算符將它依次應用在計算序列的左側便可獲得下圖左側的張量公式:

對張量（Tensor）變換即可得上圖右側的矩陣公式。其中 ，J 便是一階導 Jacobian 矩陣,這種計算導數的方式與展開的計運算元序列順序相同，所以正序模式每一個方向導數的計算複雜度與計算序列相同 空間複雜度也相同。

對於算式(1)：

y=x0∗x1+x1 （1）

如求y對x1的偏導其對應的forward-mode計算序列為：

∂x0dx1=0

∂cdx1=x0

∂ddc=1

∂ddx1=1

∂ddx1=∂ddc∂cdx1+∂x1∂x1 (sum rule)

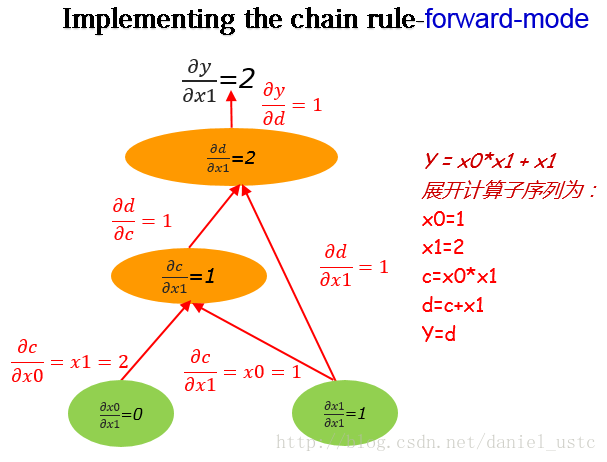
在計算圖上自底向上求關於x1的偏導，如下圖：

從圖中我們可以看出來，利用forward-mode對x1求偏導，可以得到所有節點關於x1的偏導。即forward-mode可以求出所有輸出關於某一個輸入的偏導數，注意這裡一次forward計算只得到所有輸出關於某一個自變數的偏導數，如果輸入（自變數）是n維的，想得到輸出關於其它輸入（自變數）的偏導數，則需要計算多次。
注意 若計算序列的自變數有 n 維，則獲得 Jacobian 矩陣需要計算 n 個方向上的方向導數。
2. reverse-mode
任意對偶向量 dt=tidzi 的定義是其對應方向的微分
對該向量做關於座標基 {dxi} 的座標變換 便可獲得下圖左側的張量公式:

對張量縮並可得上圖右側的矩陣公式， 其中D+=TP表示疊加 D=D+TP ，Dx便是關於x的一階導。這種計算導數的方式與計算序列逆序，所以稱為逆序模式(reverse-model)。問題來了，如何得到這種逆序方式呢？
關於如何求這種逆序模式，前人已經有所研究，Recipes for adjoint code construction, 結合論文的思路舉個例子說明吧，對於計算式：
y=x0∗x1+x1

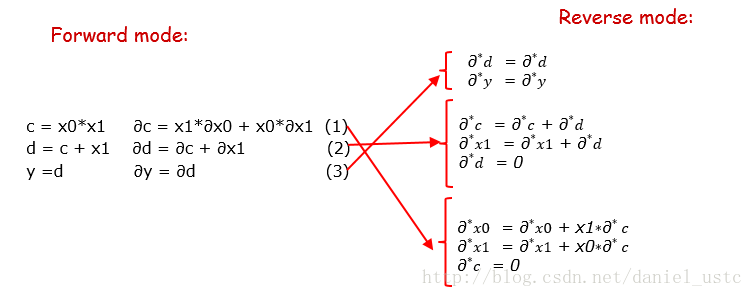
上面展開對應的子序列及其微分如下圖：

對於上面圖左側，逆序模式是對圖中右側計運算元序列的微分形式的逆序求解伴隨模式序列，然後按照伴隨模式的順序計算即可得到相關變數的偏導數，關於伴隨模式的求解方法，其實比較簡單，知道矩陣的轉置是怎麼回事就能求出adjoint code，關於上圖式(2)微分表示式及其矩陣形式如下圖：

對上圖等式右側的矩陣進行轉置即可得到式(2)對應的伴隨模式所對應的計算序列，如下圖所示：

圖中轉置矩陣展開後的三個表示式即為公式（2）對應的伴隨模式程式碼（也即逆序模式對應的程式碼），把計運算元序列的微分形式按照這種方式逆序展開即為逆序模式的計算序列，把前序模式對應的微分表示式逆序展開為伴隨表示式，即為下圖所示：

這裡注意d其實就是y的別名因此表達的意思所以一樣的，下面我們根據adjoint 計算序列來寫出reverse-mode求解偏導的程式碼：

#include <cmath>
#include <iostream>
using namespace std;

double reverse_AD(const double x[2], double y_ad[1], double x_ad[2]) {
    double c = x[0] * x[1];
    double d = c + x[1];
    double y = d;

    /* Adjoint part: */
    // init
    double d_ad = 0, c_ad = 0;

    d_ad = y_ad[0]; // 1

    c_ad = c_ad + d_ad;   // 2
    x_ad[1] = x_ad[1] + d_ad;
    d_ad = 0;

    x_ad[0] = x_ad[0] + x[1] * c_ad; // 3
    x_ad[1] = x_ad[1] + x[0]*c_ad;
    c_ad = c_ad;

    return y;
}

int main()
{
    double x[] = { 1.0, 2.0 };
    double y_ad[1] = { 1.0 };// init to 1
    double x_ad[2] = { 0, 0 };
    double y = reverse_AD(x, y_ad, x_ad);
    cout << "y=" << y << "\n";
    cout << "dy/dy=" << y_ad[0] << "\n";
    cout << "dy/dx0=" << x_ad[0] << "\n";
    cout << "dy/dx1=" << x_ad[1] << "\n";
    return 0;
}

輸出為：

y=4
dy/dy=1
dy/dx0=2
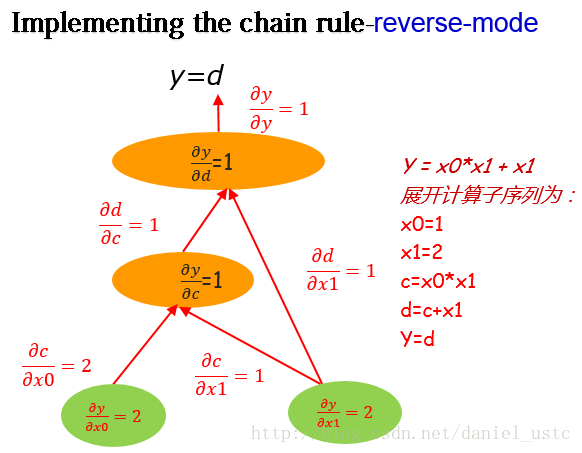
dy/dx1=2

利用reverse-mode在計算圖上從圖頂部y向下求解偏導，我們可以得到輸出關於所有節點的偏導數，如下圖：

從圖中以及上面的程式也能看出來，reverse-mode從上至下計算，我們能夠獲得輸出關於所有節點的偏導（當然包括所有自變數，即這裡的x0,x1）。 對比上面介紹的forward-mode，利用 forward-mode一次計算，我們只能得到關於某一個自變數的偏導數。因此，試想我們在機器學習中有這樣一個優化函式，它有上百萬個引數，如果利用 forward-mode求解這些引數的偏導，那麼需要計算百萬次，這是一個很耗費時間的事情，但是如果利用reverse-mode僅僅需要計算一次，我們就能得到關於所有引數的偏導數。所以基於reverse-mode的這一特性，現在流行的深度學習框架中，神級網路模型訓練的BP演算法基本也是利用reverse-mode進行求解的。

雖然reverse-mode有諸多優點，但是forward-mode也有它自身的優點（比如方法簡單易懂，不需要儲存很多中間變數，reverse-mode就需要儲存挺多中間變數的…）。因此 何時用正序模式 何時用逆序模式？
取決於自變數維度 n 與因變數維度 m，若 n > m 則逆序更快 若 n < m 則正序更快。

如何實現reverse-mode？有興趣的讀一下這篇論文：
“Fast Reverse-Mode Automatic Differentiation using Expression”

參考

1. R. Giering and T. Kaminski. 1998. Recipes for adjoint code construction. ACM Trans. Math. Softw. 24, 437–474. down
2. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation, Second Edition
3. The Art of Differentiating Computer Programs: An Introduction to Algorithmic Differentiation
4. Automatic differentiation in machine learning: a survey