這道題搞了很久終於搞懂了，感覺受益匪淺，先貼上題目：

這是一道比CCCC簡單題難的簡單題

Time Limit: 3000/1000MS (Java/Others)     Memory Limit:65535/262140KB (Java/Others)

集訓隊的CFT大爺精通Python

有一天，CFT大爺跑在vps上的python爬蟲程式掛了

CFT大爺經過縝密的推斷，發現程式掛了的原因是Python的垃圾回收機制不夠優越，導致記憶體炸了，那些賣vps的奸商強行殺掉了他的爬蟲程式

CFT大爺決定再也不用python這門垃圾語言，他要發明一個新的語言CFTthon

CFT大爺的CFTthon是跑在CFT大爺以前寫的

CFT大爺在手寫CFTthon的GC系統時，想到了一個問題：給定n,m，要求用CFTthon的變數把整個記憶體空間完全覆蓋，不重合不遺漏，有多少種方法呢？

**** 扯淡題意分割線 ****

給定一個n*m的矩陣，使用1*2的小長方形覆蓋矩陣，要求完全覆蓋的同時不出現重合，也不允許超出邊界，問有多少種可能的覆蓋方法,方案數對1e9+7取模

2<=n<=1000

3<=m<=5

Input

整數n,m

Output

方案數

Sample input and output

2 4

5

描述

歷經千辛萬苦，小Hi和小Ho終於到達了舉辦美食節的城市！雖然人山人海，但小Hi和小Ho仍然抑制不住興奮之情，他們放下行李便投入到了美食節的活動當中。美食節的各個攤位上各自有著非常多的有意思的小遊戲，其中一個便是這樣子的：

小Hi和小Ho領到了一個大小為N*M的長方形盤子，他們可以用這個盒子來裝一些大小為2*1的蛋糕。但是根據要求，他們一定要將這個盤子裝的滿滿的，一點縫隙也不能留下來，才能夠將這些蛋糕帶走。

這麼簡單的問題自然難不倒小Hi和小Ho，於是他們很快的就拿著蛋糕離開了~

但小Ho卻不只滿足於此，於是他提出了一個問題——他們有多少種方案來裝滿這個N*M的盤子呢？

值得注意的是，這個長方形盤子的上下左右是有區別的，如在N=4, M=3的時候，下面的兩種方案被視為不同的兩種方案哦！

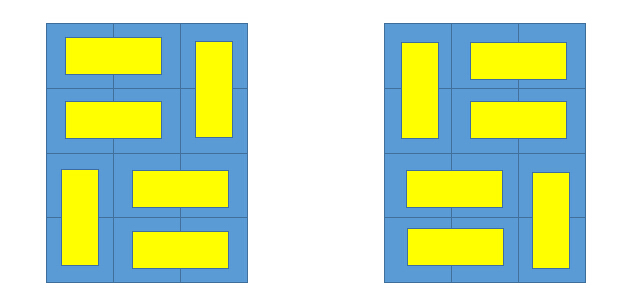
輸入

每個測試點（輸入檔案）有且僅有一組測試資料。

每組測試資料的第一行為兩個正整數N、M，表示小Hi和小Ho拿到的盤子的大小。

對於100%的資料，滿足2<=N<=1000, 3<=m<=5。

輸出

考慮到總的方案數可能非常大，只需要輸出方案數除以1000000007的餘數。

分析：

其實這兩道題本質是完全一樣的，就是用1*2的小長方形完全覆蓋n * m的矩形有多少方案。

下面分析如何用狀態壓縮DP來解這道題(如果不理解為什麼要用DP，為什麼要用狀壓DP見hihoCoder題目中的提示連結，雖然我也看得雲裡霧裡)

DP顧名思義，我們需要用到狀態轉移，假設我們現在正在考慮(i,j)這個位置該怎麼放(此時這個位置之前的位置已經鋪好了)。有三種情況：

1. 不需要鋪磚，因為在位置(i-1,j)鋪的是豎磚，(i,j)已經被鋪好了。(為什麼不用考慮(i,j-1)鋪橫磚在下面會解釋)
2. 鋪橫磚，那麼(i,j+1)也就被同時鋪好了，直接考慮(i,j+2),這正解釋了(1)中為什麼不用考慮(i,j-1)鋪橫磚的情況。
3. 鋪豎磚，那麼(i+1,j)也就被同時鋪好了.

鑑於以上幾種情況，我們將每一個位置的狀態用0或1來表示，如果我們在(i,j)鋪橫磚，那麼(i,j)和(i,j+1)都為1，如果我們在(i,j)鋪豎磚，那麼(i,j)為0，(i,j+1)為1。

可以用下面的圖片增進理解：

那為什麼要這樣定義呢，我們可以這麼認為，某一個位置的狀態為1則表示它對下一行的狀態沒有限制，而為0時，表示它對下一行的狀態有限制(必須為1)。(讀者可以將上面的兩種情況自己模擬一下)

然後下一步我們要做的就是對每個位置的放置方法進行檢測可行性，並對它計數。

我們先用一個數來表示某一行的狀態，這個數轉化為二進位制數後，第i個數*(0/1)代表該行第i列的狀態。我們需要做的便是判斷相鄰行的狀態是否合法。

判斷方法的解析見程式碼中的註釋。

由於第一行沒有前驅，我們先對第一行進行特判，然後再從第二行開始進行狀態轉移。

用dp[i][j]表示鋪到第i行，且第i行的狀態為j時的總方案數。容易寫出狀態轉移方程為dp[i][j]=dp[i][j]+dp[i-1][k]（dp[i][j]一定等於i-1行能與j狀態相容的所有方案數和）

由於最後一行的狀態不可能出現0，所以結果就是dp[n-1][total-1],

（計算過程中注意取模）

#include <cstdio>
#include <cmath>
#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;
#define mst(a,b) memset((a),(b),sizeof(a))
#define f(i,a,b) for(int i=(a);i<=(b);++i)
#define rush() int T;scanf("%d",&T);while(T--)

typedef long long ll;
const int maxn= 1005;
const ll mod = 1e9+7;
const int INF = 0x3f3f3f3f;
const double eps = 1e-6;

ll dp[maxn][1<<5];

bool one(int state,int len)    //檢測某一行內部的狀態是否滿足要求
{
    int pos=0;
    while(pos<len)
    {
        if((state&(1<<pos))==0)  //如果這一位為0，說明這一格是豎鋪的，檢測下一位置
            pos++;
        //其餘情況都是橫鋪的,即當前pos和pos+1的狀態都為1
        //噹噹前pos已經是最右邊的或者pos+1的狀態不為1
        else if(pos==len-1||!(state&(1<<(pos+1))))
            return false;
        //滿足條件就跳過對pos+1的檢測
        else pos+=2;
    }
    return true;
}

bool two(int state_pre,int state_now,int len)  //檢測相鄰行的狀態是否滿足要求
{
    int pos=0;
    while(pos<len)
    {
        if((state_pre&(1<<pos))==0)   //前一行為0，說明是豎鋪，這一行的對應位置必須為1
        {
            if((state_now&(1<<pos))==0)
                return false;
            pos++;
            continue;
        }
        if((state_now&(1<<pos))==0)  //同上
            pos++;
        //當前位置為1，則下一位置必須為1，且下一位置對應的前一行必須為0(豎放)
        else if(pos==len-1||!((state_pre&(1<<(pos+1)))&&(state_now&(1<<(pos+1)))))
            return false;
        else pos+=2;
    }
    return true;
}

int main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        if(m>n)          //優化，因為此題時間、空間主要消耗在每一行的多種狀態上
            swap(m,n);
        int total=1<<m;  //一行的所有狀態數
        mst(dp,0);
        for(int i=0;i<total;i++)
        {
            if(one(i,m))
            {
                dp[0][i]=1;
            }
        }
        for(int i=1;i<n;i++)
        for(int j=0;j<total;j++)     //當前一行的狀態
        for(int k=0;k<total;k++)     //前一行的狀態
        {
            if(two(j,k,m))
            {
                dp[i][j]=(dp[i][j]+dp[i-1][k])%mod;
            }
        }
        printf("%lld\n",dp[n-1][total-1]);
    }
    return 0;
}