圖的基礎知識學習(一)
終於決定學一下圖了,圖一直以為是一種蠻有意思的方法。
圖G=(V,E),V表示頂點數,E表示邊數,圖可以分為有向圖和無向圖,有兩種標準的方法,即鄰接表和鄰接矩陣。
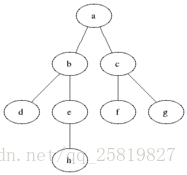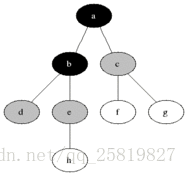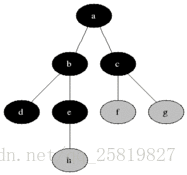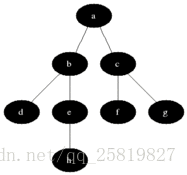
鄰接表有V個列表的Adj陣列組成,Adj[u]包含圖G中的所有和頂點u相連的頂點,在無向圖中的順序是任意的,在有向圖中和圖的方向有關。鄰接矩陣在無向圖中為頂點的點為1,其餘為零,有向圖中則和方向有關,如下圖所示。
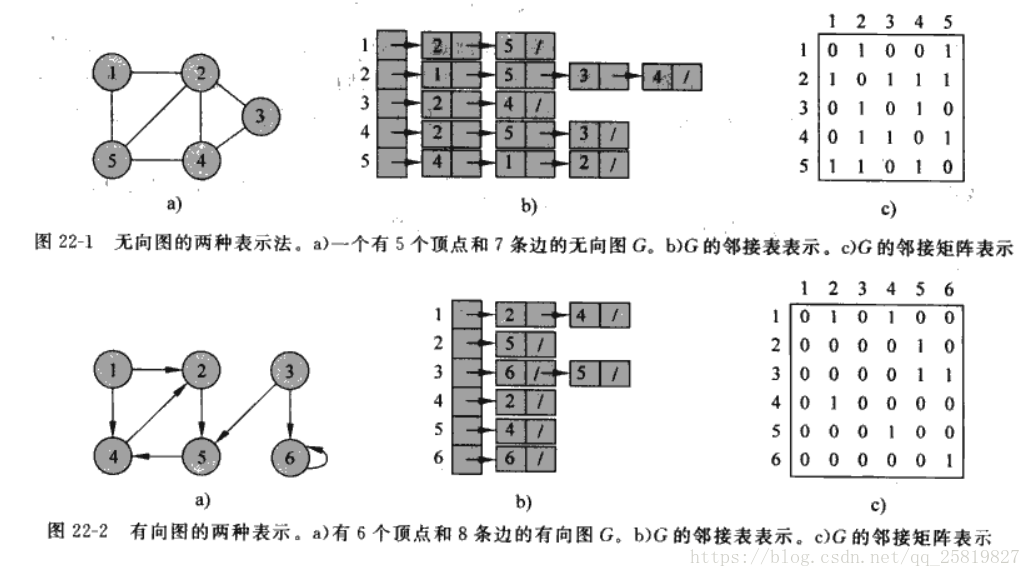
鄰接表無論是有向圖還是無向圖的儲存空間都為O(V+E),但有潛在的不足及,要搜尋邊(u,v)是否存在只能在Adj[u]陣列中搜索v;鄰接矩陣的儲存空間為,所需的儲存空間較大,但搜尋邊(u,v)的速度較快。對於無向圖的鄰接矩陣,如上圖所示為一個對稱矩陣,儲存空空間可以再縮小一半。
圖搜尋演算法主要分為兩種:廣度優先演算法和深度優先演算法
廣度優先演算法(BFS)中:
對於給定的圖G和源頂點s,優先對s的相鄰邊進行搜尋,以求發現所有s可以到達的頂點,同時還能生成一顆根為s,包含所有s能到達的廣度優先樹,適用於無向圖和有向圖。廣度優先演算法先發現與發現點與未發現的點之間的邊界,沿其廣度方向向外擴充套件,即會先發現1所有距離為k的點然後發現距離為k+1的點。
如下圖所示:
程式碼(來自維基百科):
def breadth_first_search(problem):
# a FIFO open_set
open_set = Queue()
# an empty set to maintain visited nodes
closed_set = set()
# a dictionary to maintain meta information (used for path formation)
# key -> (parent state, action to reach child)
meta = dict()
# initialize 深度優先演算法(DSF):
在演算法的搜尋過程中,對於發現的新的頂點,如果它還有以此為起點而未探測到的邊,就研此邊搜尋下去。當頂點v的所有邊都被搜尋後回到發現v頂點那邊開始搜尋其他邊,直到所有的頂點都被搜尋完。
下面是深度優先演算法的虛擬碼:
這裡設定兩個時間戳d[v],f[v],d[v]表示發現點v,f[v]表示結束髮現點v,這裡設定未發現點v為白色,發現後變灰色,結束搜尋點v所在的支路後為黑色;
DFS(G)
for each vertes u∈V[G]
do color[u]<- WHITE
π[u]<-NIL
time<-0
for each vertex u∈V[G]
do if color[u]=WHITE
then DFS-VISIT(u)
DFS-VISIT(u)
color[u]<-GRAY
time<-time+1
d[u]<-time+1
for each v∈Adj[u]
do if color[v]=WHITE
then π[v]<-u
DFS-VISIT(v)
color[u]<-BLACK
f[u]<-time<-time+1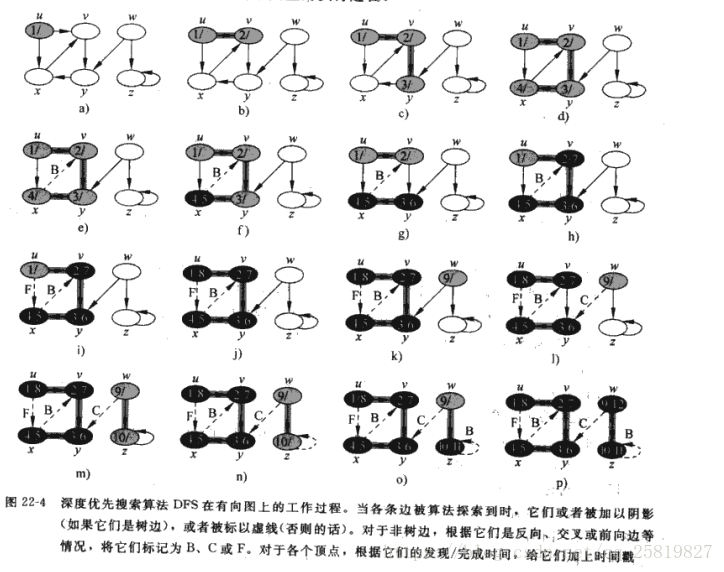
先初始化整個圖為白色,π域為NIL,置定時器為0,再依次檢索V中的頂點,當發現白色頂點時呼叫DFS-VISIT訪問。
呼叫DFS-VISIT時置u為灰色,增加time的值,記錄發現u的值,再檢查和u相鄰的頂點v如果為白色則遞迴呼叫DFS-VISIT,當以u為起點的所有邊都被搜尋後值u為黑色,並記錄時間在f[u].