設計一個演算法,輸出從u到v的所有最短路徑(採用鄰接表儲存)
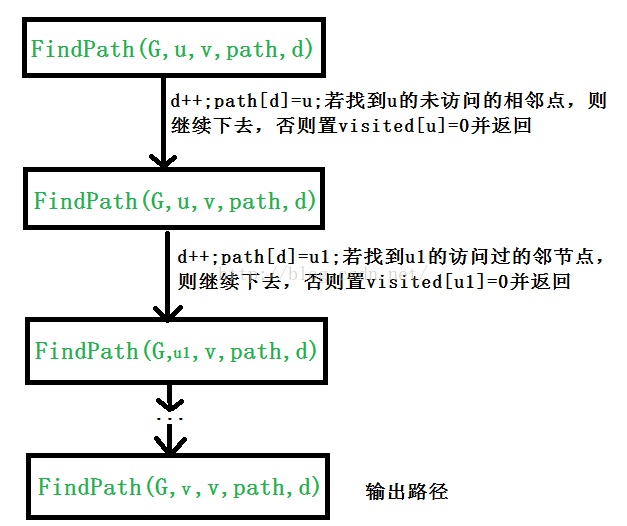
思想:用path陣列存放路徑(初始為空),d表示路徑長度(初始為-1),查詢從頂點u到v的最短路徑過程如圖所示:
對應演算法如下:
void FindPath(AGraph *G,int u,int v,int path[ ],int d)
{
int w,i;
ArcNode *p;
d++;
path[d]=u;
visited[u]=1;//路徑長度增1
if(u==v)
{
for(i=0;i<=d;i++)
printf("%2d",path[i]);
printf("\n");
}
p=G->adjlist[u].firstarc;//p指向v的第一個相鄰點
while(p!=NULL)
{
w=p->adjvex;
if(visited[w]==0)//若w頂點未訪問,遞迴訪問它
FindPath(G,w,v,path,d);
p=p->nextarc;//p指向v的下一個鄰接點
}
visited[u]=0;//恢復環境,使該頂點可重新使用
}
相關推薦
設計一個演算法,輸出從u到v的所有最短路徑(採用鄰接表儲存)
思想:用path陣列存放路徑(初始為空),d表示路徑長度(初始為-1),查詢從頂點u到v的最短路徑過程如圖所示: 對應演算法如下: void FindPath(
Dijkstra演算法,有權單源最短路徑
與無權單源最短路徑相似,與層次遍歷相似;以遞增的順序依次收錄遇到的最短距離的頂點 int findmin(Graph G,int dist[],int collected[]) // 找到一個未被收錄的最小值 { int Min = MAXNUM; // 儲存最小值,初值為無窮大;
圖之從一個頂點到其餘各個頂點的最短路徑(有向圖)
目錄 從一個頂點到其餘各個頂點最短路徑的簡介 舉例以及詳細分析 程式碼塊 測試結果 從一個頂點到其餘各個頂點最短路徑的簡介(又名單元最短路徑) 1.定義概覽 Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法,用於計算一個節點到其他所
設計一個演算法,刪除遞增有序連結串列中值大於mink且小於maxk的所有元素(mink和maxk是給定的兩個引數,其值可以和表中的元素相同,也可以不同)。
語言:C++ #include <iostream> using namespace std; typedef struct LNode { int data; LNode *next; }LNode,*LinkList; //建立連結串列 int CreateList(Li
設計一個演算法,將連結串列中所有結點的連結串列方向“原地”逆轉,即要求僅利用原表的儲存空間,換句話說,要求演算法的空間複雜度為O(1)。
語言:C++ #include <iostream> using namespace std; typedef struct LNode { int data; LNode *next; }LNode,*LinkList; //建立連結串列 int CreateList(Li
設計一個演算法,通過一趟遍歷確定長度為n的單鏈表中值最大的結點。
語言:C++ #include <iostream> using namespace std; typedef int Elemtype; typedef struct LNode { Elemtype data; struct LNode *next; }LNode,*Lin
已知兩個連結串列A和B分別表示兩個集合,其元素遞增排列。請設計一個演算法,用於求出A與B的交集,並存放在A連結串列中。
語言:C++ #include <iostream> using namespace std; typedef struct LNode { int data; LNode *next; }LNode,*LinkList; //建立連結串列 int CreateList(Li
給定陣列a[0:n-1]試設計一個演算法,在最壞情況下用[3n/2 -2 ] 次比較找出a[0:n-1]中元素的最大值和最小值;教材2-15
給定陣列a[0:n-1]試設計一個演算法,在最壞情況下用[3n/2 -2 ] 次比較找出a[0:n-1]中元素的最大值和最小值; 解:要求對於陣列用小於【3n/2-2】的比較次數找到兩個最值 可以用陣列第一個元素來初始化max,min 然後遍歷陣列,分別和max,min比較,一遍就可以找
演算法題,輸入一個矩陣,輸出每一列最大的兩個數
#include <iostream> using namespace std; void search(int a[][5] , int n){ //一個5行5列的矩陣 int max[2][5]; //分別表示前一個最大的數和後一個最大的數
設計一個演算法,將一個十進位制的數轉化為二進位制
#include<iostream.h> const int StackSize=10; class SeqStack { public: SeqStack(){
程式基本演算法習題解析 用分治法設計一個演算法,找出偽造硬幣
題目: 一個裝有16枚硬幣的袋子,16枚硬幣中有一個是偽造的,並且那個偽造的硬幣比真的硬幣要輕。現有一臺可用來比較兩組硬幣重量的儀器,請使用分治法設計一個演算法,可以找出那枚偽造的硬幣。 首先建立一個有16個int資料型別的陣列,模擬16枚硬幣,真幣賦為1,假幣賦為0。根據二分搜
程式基本演算法習題解析 用分治法設計一個演算法,統計輸入的非空字串中給定字元的個數
首先附上一般思路的程式碼(不用分治法,將輸入字串中的字元從前往後依次比對): // Chapter7_1.cpp : Defines the entry point for the application. // 用分治法設計一個演算法,統計輸入的非空字串中給定字元的個數 #include "
已知線性表中元素以值遞增有序排列,並以單鏈表作為儲存結構,設計一個演算法,刪除表中值相同的多餘元素
/* 已知線性表中元素以值遞增有序排列,並以單鏈表作為儲存結構 * 設計一個演算法,刪除表中值相同的多餘元素 * 使得操作後表中所用元素值均不同,同時釋放被刪除的結點空間 */ #include<stdio.h> #inclu
【資料結構 C描述】設計一個演算法,用於檢測給定的字串是否為對稱串。
【資料結構 C描述】設計一個演算法,用於檢測給定的字串是否為對稱串。 所謂對稱串,就是字串從左往右讀和從右往左讀的序列一樣。 例如: abccba是對稱串。 abcabc不是對稱串。 //main.cpp #include <iostream> #include
程式設計師面試金典: 9.4樹與圖 4.2給定有向圖,設計一個演算法,找出兩個節點之間是否存在一條路徑。
#include <iostream> #include <stdio.h> #include <vector> #include <queue> using namespace std; /* 問題:給定有向圖,設計一個
設計一個演算法,計算出n階乘中尾部零的個數
考慮到只要有5,或者因子為5的數,就可以產生0的尾部。假如1*2*3*4*...*250,那麼250/5=50可以知道,有50個為5的倍數,但是裡面有多少個為25的倍數,125的倍數..., 50/5=10,可知25的倍數有10個,10/5=2,可知125的倍數有兩個,以此
設計一個演算法,判斷一個二叉樹是否為完全二叉樹
思想:根據完全二叉樹的定義,對完全二叉樹按照從上到下、從左到右的層次遍歷,應該滿足一下兩條要求: ●某節點沒有左孩子,則一定無右孩子 ●若某節點缺左或右孩子,則其所有後繼一定無孩子 若不滿足上述任何一
設計一個程式,輸出在順序表中採用折半找法查詢關鍵字的過程
#include"iostream" #include"algorithm" using namespace std; class list{ private: int data[20]; int
給定一個集合,輸出它的所有子集
題目:集合是由大字字母(A-Z)組成的,要求輸出集合的所有子集,每個子集一行,不能使用遞迴。 例如 “ABD”的子集: NULL(空集)、A、B、C、AB、AC、BC、ABC(共8個) 這個題可以用點陣圖的思想做。 比如集合{A,B} 對應位向量v=000...0001
【Python】設計一個演算法,計算出n階乘中尾部零的個數
1.常見的思路:先求N的階乘,再計算零的個數。 (但是,時間消耗太大) def trailingZeros( n): S = 1 for i in range(1,n+1): S = S * i