二叉樹（Binary Tree）

定義：一棵二叉樹是結點的一個有限集合，該集合或者為空，或者是由一個根結點加上兩棵分別稱為左子樹和右子樹的、互不相交的二叉樹組成。

特點：每個結點至多隻有兩棵子樹（二叉樹中不存在度大於2的結點）

五種形態：

1. 性質1

性質1  在二叉樹的第 i 層至多有 2^(i －1)個結點。(i>=1)

[用數學歸納法證明]

       證明：當i=1時，只有根結點，2^(i －1)=2^0=1。

       1) 設：對所有j，i>j>=1，命題成立，即第j層上至多有2^(j-1)個結點。

       2) 由歸納假設第i-1層上至多有2^(i－2)個結點。

       3) 由於二叉樹的每個結點的度至多為2，故在第i層上的最大結點數為第i-1層上的最大結點數的2倍，即2* 2^(i－2)= 2^(i-1) 

證畢。

2. 性質2

性質2  深度為 k 的二叉樹至多有 2^(k-1)個結點(k >=1)。

       證明：由性質1可見，深度為k的二叉樹的最大結點數為 

3. 性質3

性質3  對任何一棵二叉樹T, 如果其葉結點數為n0, 度為2的結點數為 n2,則n0＝n2＋1。

       證明：若度為1的結點有 n1個，總結點個數為n，總邊數為 e，則根據二叉樹的定義，

            n = n0 + n1 + n2    

            e = 2n2 + n1 = n - 1 (除了根節點，每個節點對應一條邊 )

           因此，有  2n2+ n1 =n0 + n1 + n2- 1

                          n2= n0 - 1  =>   n0= n2+ 1

          空鏈域：2n0+ n1 = n0 + n2 +1+ n1 = n+1

4. 性質4

性質4  具有 n (n>=0) 個結點的完全二叉樹的深度為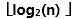＋1 

       證明：設完全二叉樹的深度為 h，則根據性質2 和完全二叉樹的定義有

            2^(h－1)- 1 < n <= 2^h - 1或 2^(h－1)<= n < 2^h

               取對數 h－1 < log2n  <= h，又h是整數，

               因此有 h = 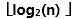＋1 

5. 性質5

性質5  如將一棵有n個結點的完全二叉樹自頂向下，同層自左向右連續為結點編號0,1, …, n-1，則有： 

       1）若i = 0, 則 i 無雙親,   若i > 0, 則 i 的雙親為」(i -1)/2」

       2）若2*i+1 < n, 則i 的左子女為 2*i+1，若2*i+2 < n, 則 i 的右子女為2*i+2

       3）若結點編號i為偶數，且i != 0,則左兄弟結點i-1.

       4）若結點編號i為奇數，且i != n-1,則右兄弟結點為i+1.

       5）結點i 所在層次為」log2(i+1) 」

參考資料：

1. Boss的PPT