這學期選了門模式識別的課。發現最常見的一種情況就是，書上寫的老師ppt上寫的都看不懂，然後繞了一大圈去自己查資料理解，回頭看看發現，Ah-ha，原來本質的原理那麼簡單，自己一開始只不過被那些看似formidable的細節嚇到了。所以在這裡把自己所學的一些點記錄下來，供備忘，也供參考。

1. K-Nearest Neighbor

K-NN可以說是一種最直接的用來分類未知資料的方法。基本通過下面這張圖跟文字說明就可以明白K-NN是幹什麼的

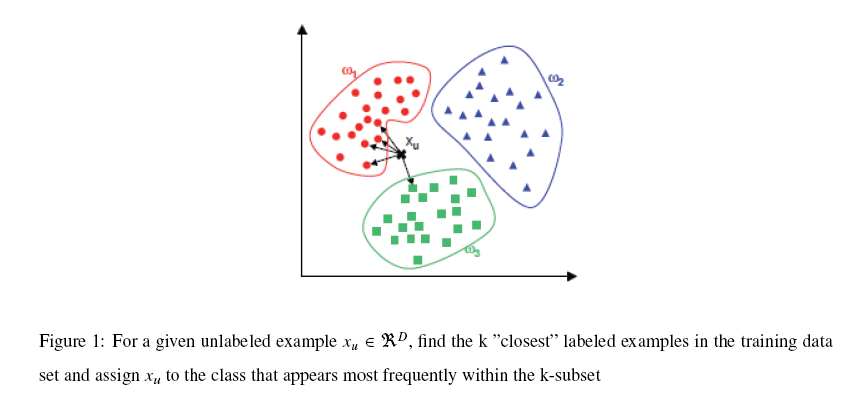
簡單來說，K-NN可以看成：有那麼一堆你已經知道分類的資料，然後當一個新資料進入的時候，就開始跟訓練資料裡的每個點求距離，然後挑離這個訓練資料最近的K個點看看這幾個點屬於什麼型別，然後用少數服從多數的原則，給新資料歸類。一個比較好的介紹k-NN的課件可以見下面連結，圖文並茂，我當時一看就懂了

實際上K-NN本身的運算量是相當大的，因為資料的維數往往不止2維，而且訓練資料庫越大，所求的樣本間距離就越多。就拿我們course project的人臉檢測來說，輸入向量的維數是1024維(32x32的圖，當然我覺得這種方法比較silly)，訓練資料有上千個，所以每次求距離(這裡用的是歐式距離，就是我們最常用的平方和開根號求距法) 這樣每個點的歸類都要花上上百萬次的計算。所以現在比較常用的一種方法就是kd-tree。也就是把整個輸入空間劃分成很多很多小子區域，然後根據臨近的原則把它們組織為樹形結構。然後搜尋最近K個點的時候就不用全盤比較而只要比較臨近幾個子區域的訓練資料就行了。kd-tree的一個比較好的課件可以見下面連結：

當然，kd-tree有一個問題就是當輸入維數跟訓練資料數量很接近時就很難優化了。所以用PCA(稍後會介紹)降維大多數情況下是很有必要的 2. Bayes Classifier 在模式識別的實際應用中，貝葉斯方法絕非就是post正比於prior*likelihood這個公式這麼簡單，一般而言我們都會用正態分佈擬合likelihood來實現。 用正態分佈擬合是什麼意思呢？貝葉斯方法式子的右邊有兩個量，一個是prior先驗概率，這個求起來很簡單，就是一大堆資料中求某一類資料佔的百分比就可以了，比如300個一堆的資料中A類資料佔100個，那麼A的先驗概率就是1/3。第二個就是likelihood，likelihood可以這麼理解：對於每一類的訓練資料，我們都用一個multivariate正態分佈來擬合它們(即通過求得某一分類訓練資料的平均值和協方差矩陣來擬合出一個正態分佈)，然後當進入一個新的測試資料之後，就分別求取這個資料點在每個類別的正態分佈中的大小，然後用這個值乘以原先的prior便是所要求得的後驗概率post了。 貝葉斯公式中還有一個evidence，對於初學者來說，可能會一下沒法理解為什麼在實際運算中它不見了。實則上，evidence只是一個讓最後post歸一化的東西，而在模式分類中，我們只需要比較不同類別間post的大小，歸一化反而增加了它的運算量。當然，在有的地方，這個evidence絕對不能省，比如後文提到的GMM中，需要用到EM迭代，這時候如果不用evidence將post歸一化，後果就會很可怕。 Bayes方法一個不錯的參考網頁可見下面連結： 3. Principle Component Analysis PCA，譯為主元分析或者主成份分析，是一種很好的簡化資料的方法，也是PR中常見到不能再常見的演算法之一。CSDN上有一篇很不錯的中文部落格介紹PCA，《主元分析(PCA)理論分析及應用》，可以見下面連結： 對於我而言，主元分析最大的意義就是讓我明白了線性代數中特徵值跟特徵向量究竟代表什麼，從而讓我進一步感受到了線性代數的博大精深魅力無窮。- -||| PCA簡而言之就是根據輸入資料的分佈給輸入資料重新找到更能描述這組資料的正交的座標軸，比如下面一幅圖，對於那個橢圓狀的分佈，最方便表示這個分佈的座標軸肯定是橢圓的長軸短軸而不是原來的x y。 那麼如何求出這個長軸和短軸呢？於是線性代數就來了：我們求出這堆資料的協方差矩陣(關於什麼是協方差矩陣，詳見本節最後附的連結)，然後再求出這個協方差矩陣的特徵值和特徵向量，對應最大特徵值的那個特徵向量的方向就是長軸(也就是主元)的方向，次大特徵值的就是第二主元的方向，以此類推。 關於PCA，推薦兩個不錯的tutorial: (1) A tutorial on Principle Component Analysis從最基本的數學原理到應用都有，讓我在被老師的講課弄暈之後瞬間開悟的tutorial: (2) 裡面有一個很生動的實現PCA的例子，還有告訴你PCA跟SVD是什麼關係的，對程式設計實現的幫助很大(當然大多數情況下都不用自己編了):

4. Linear Discriminant Analysis

LDA，基本和PCA是一對雙生子，它們之間的區別就是PCA是一種unsupervised的對映方法而LDA是一種supervised對映方法，這一點可以從下圖中一個2D的例子簡單看出

圖的左邊是PCA，它所作的只是將整組資料整體對映到最方便表示這組資料的座標軸上，對映時沒有利用任何資料內部的分類資訊。因此，雖然做了PCA後，整組資料在表示上更加方便(降低了維數並將資訊損失降到最低)，但在分類上也許會變得更加困難；圖的右邊是LDA，可以明顯看出，在增加了分類資訊之後，兩組輸入對映到了另外一個座標軸上，有了這樣一個對映，兩組資料之間的就變得更易區分了(在低維上就可以區分，減少了很大的運算量)。

在實際應用中，最常用的一種LDA方法叫作Fisher Linear Discriminant，其簡要原理就是求取一個線性變換，是的樣本資料中“between classes scatter matrix”(不同類資料間的協方差矩陣)和“within classes scattermatrix”(同一類資料內部的各個資料間協方差矩陣)之比的達到最大。關於Fisher LDA更具體的內容可以見下面課件，寫的很不錯~

5. Non-negative Matrix Factorization

NMF，中文譯為非負矩陣分解。一篇比較不錯的NMF中文介紹文可以見下面一篇博文的連結，《非負矩陣分解：數學的奇妙力量》

這篇博文很大概地介紹了一下NMF的來龍去脈(當然裡面那幅圖是錯的。。。)，當然如果你想更深入地瞭解NMF的話，可以參考Lee和Seung當年發表在Nature上面的NMF原文，”Learning the parts of objects by non-negative matrix factorization”

讀了這篇論文，基本其他任何介紹NMF基本方法的材料都是浮雲了。

NMF，簡而言之，就是給定一個非負矩陣V，我們尋找另外兩個非負矩陣W和H來分解它，使得後W和H的乘積是V。論文中所提到的最簡單的方法，就是根據最小化||V-WH||的要求，通過Gradient Discent推匯出一個update rule，然後再對其中的每個元素進行迭代，最後得到最小值，具體的update rule見下圖，注意其中Wia等帶下標的符號表示的是矩陣裡的元素，而非代表整個矩陣，當年在這個上面繞了好久。。

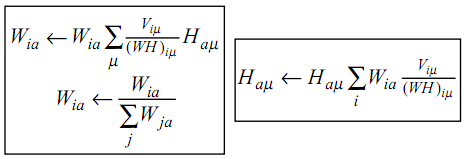
相比於PCA、LDA，NMF有個明顯的好處就是它的非負，因為為在很多情況下帶有負號的運算算起來都不這麼方便，但是它也有一個問題就是NMF分解出來的結果不像PCA和LDA一樣是恆定的。

6. Gaussian Mixture Model

GMM高斯混合模型粗看上去跟上文所提的貝葉斯分類器有點類似，但兩者的方法有很大的不同。在貝葉斯分類器中，我們已經事先知道了訓練資料(training set)的分類資訊，因此只要根據對應的均值和協方差矩陣擬合一個高斯分佈即可。而在GMM中，我們除了資料的資訊，對資料的分類一無所知，因此，在運算時我們不僅需要估算每個資料的分類，還要估算這些估算後資料分類的均值和協方差矩陣。。。也就是說如果有1000個訓練資料10租分類的話，需要求的未知數是1000+10+10(用未知數表示未必確切，確切的說是1000個1x10標誌向量,10個與訓練資料同維的平均向量，10個與訓練資料同維的方陣)。。。反正想想都是很頭大的事情。。。那麼這個問題是怎麼解決的呢？

這裡用的是一種叫EM迭代的方法。

當然 Matlab裡一般也會自帶GMM工具箱，其用法可以參考下面連結：