先明確一點就是，Deep Learning是全部深度學習演算法的總稱，CNN是深度學習演算法在影象處理領域的一個應用。

第一點，在學習Deep learning和CNN之前，總以為它們是很了不得的知識，總以為它們能解決很多問題，學習了之後，才知道它們不過與其他機器學習演算法如svm等相似，仍然可以把它當做一個分類器，仍然可以像使用一個黑盒子那樣使用它。

第二點，Deep Learning強大的地方就是可以利用網路中間某一層的輸出當做是資料的另一種表達，從而可以將其認為是經過網路學習到的特徵。基於該特徵，可以進行進一步的相似度比較等。

第三點，Deep Learning演算法能夠有效的關鍵其實是大規模的資料，這一點原因在於每個DL都有眾多的引數，少量資料無法將引數訓練充分。

接下來話不多說，直接奔入主題開始CNN之旅。

卷積神經網路簡介（Convolutional Neural Networks，簡稱CNN）

卷積神經網路是近年發展起來，並引起廣泛重視的一種高效識別方法。20世紀60年代，Hubel和Wiesel在研究貓腦皮層中用於區域性敏感和方向選擇的神經元時發現其獨特的網路結構可以有效地降低反饋神經網路的複雜性，繼而提出了卷積神經網路（Convolutional Neural Networks-簡稱CNN）。現在，CNN已經成為眾多科學領域的研究熱點之一，特別是在模式分類領域，由於該網路避免了對影象的複雜前期預處理，可以直接輸入原始影象，因而得到了更為廣泛的應用。 K.Fukushima在1980年提出的新識別機是卷積神經網路的第一個實現網路。隨後，更多的科研工作者對該網路進行了改進。其中，具有代表性的研究成果是Alexander和Taylor提出的“改進認知機”，該方法綜合了各種改進方法的優點並避免了耗時的誤差反向傳播。

一般地，CNN的基本結構包括兩層，其一為特徵提取層，每個神經元的輸入與前一層的區域性接受域相連，並提取該區域性的特徵。一旦該區域性特徵被提取後，它與其它特徵間的位置關係也隨之確定下來；其二是特徵對映層，網路的每個計算層由多個特徵對映組成，每個特徵對映是一個平面，平面上所有神經元的權值相等。特徵對映結構採用影響函式核小的sigmoid函式作為卷積網路的啟用函式，使得特徵對映具有位移不變性。此外，由於一個對映面上的神經元共享權值，因而減少了網路自由引數的個數。卷積神經網路中的每一個卷積層都緊跟著一個用來求區域性平均與二次提取的計算層，這種特有的兩次特徵提取結構減小了特徵解析度。

CNN主要用來識別位移、縮放及其他形式扭曲不變性的二維圖形。由於CNN的特徵檢測層通過訓練資料進行學習，所以在使用CNN時，避免了顯示的特徵抽取，而隱式地從訓練資料中進行學習；再者由於同一特徵對映面上的神經元權值相同，所以網路可以並行學習，這也是卷積網路相對於神經元彼此相連網路的一大優勢。卷積神經網路以其區域性權值共享的特殊結構在語音識別和影象處理方面有著獨特的優越性，其佈局更接近於實際的生物神經網路，權值共享降低了網路的複雜性，特別是多維輸入向量的影象可以直接輸入網路這一特點避免了特徵提取和分類過程中資料重建的複雜度。

1. 神經網路

首先介紹神經網路，這一步的詳細可以參考資源1。簡要介紹下。神經網路的每個單元如下：

其對應的公式如下：

其中，該單元也可以被稱作是Logistic迴歸模型。當將多個單元組合起來並具有分層結構時，就形成了神經網路模型。下圖展示了一個具有一個隱含層的神經網路。

其對應的公式如下：

比較類似的，可以拓展到有2,3,4,5，…個隱含層。

神經網路的訓練方法也同Logistic類似，不過由於其多層性，還需要利用鏈式求導法則對隱含層的節點進行求導，即梯度下降+鏈式求導法則，專業名稱為反向傳播。關於訓練演算法，本文暫不涉及。

2 卷積神經網路

在影象處理中，往往把影象表示為畫素的向量，比如一個1000×1000的影象，可以表示為一個1000000的向量。在上一節中提到的神經網路中，如果隱含層數目與輸入層一樣，即也是1000000時，那麼輸入層到隱含層的引數資料為1000000×1000000=10^12，這樣就太多了，基本沒法訓練。所以影象處理要想練成神經網路大法，必先減少引數加快速度。就跟辟邪劍譜似的，普通人練得很挫，一旦自宮後內力變強劍法變快，就變的很牛了。

2.1 區域性感知

卷積神經網路有兩種神器可以降低引數數目，第一種神器叫做區域性感知野。一般認為人對外界的認知是從區域性到全域性的，而影象的空間聯絡也是區域性的畫素聯絡較為緊密，而距離較遠的畫素相關性則較弱。因而，每個神經元其實沒有必要對全域性影象進行感知，只需要對區域性進行感知，然後在更高層將區域性的資訊綜合起來就得到了全域性的資訊。網路部分連通的思想，也是受啟發於生物學裡面的視覺系統結構。視覺皮層的神經元就是區域性接受資訊的（即這些神經元只響應某些特定區域的刺激）。如下圖所示：左圖為全連線，右圖為區域性連線。

在上右圖中，假如每個神經元只和10×10個畫素值相連，那麼權值資料為1000000×100個引數，減少為原來的千分之一。而那10×10個畫素值對應的10×10個引數，其實就相當於卷積操作。

2.2 引數共享

但其實這樣的話引數仍然過多，那麼就啟動第二級神器，即權值共享。在上面的區域性連線中，每個神經元都對應100個引數，一共1000000個神經元，如果這1000000個神經元的100個引數都是相等的，那麼引數數目就變為100了。

怎麼理解權值共享呢？我們可以這100個引數（也就是卷積操作）看成是提取特徵的方式，該方式與位置無關。這其中隱含的原理則是：影象的一部分的統計特性與其他部分是一樣的。這也意味著我們在這一部分學習的特徵也能用在另一部分上，所以對於這個影象上的所有位置，我們都能使用同樣的學習特徵。

更直觀一些，當從一個大尺寸影象中隨機選取一小塊，比如說 8×8 作為樣本，並且從這個小塊樣本中學習到了一些特徵，這時我們可以把從這個 8×8 樣本中學習到的特徵作為探測器，應用到這個影象的任意地方中去。特別是，我們可以用從 8×8 樣本中所學習到的特徵跟原本的大尺寸影象作卷積，從而對這個大尺寸影象上的任一位置獲得一個不同特徵的啟用值。

如下圖所示，展示了一個33的卷積核在55的影象上做卷積的過程。每個卷積都是一種特徵提取方式，就像一個篩子，將影象中符合條件（啟用值越大越符合條件）的部分篩選出來。

2.3 多卷積核

上面所述只有100個引數時，表明只有1個100*100的卷積核，顯然，特徵提取是不充分的，我們可以新增多個卷積核，比如32個卷積核，可以學習32種特徵。在有多個卷積核時，如下圖所示：

上圖右，不同顏色表明不同的卷積核。每個卷積核都會將影象生成為另一幅影象。比如兩個卷積核就可以將生成兩幅影象，這兩幅影象可以看做是一張影象的不同的通道。如下圖所示，下圖有個小錯誤，即將w1改為w0，w2改為w1即可。下文中仍以w1和w2稱呼它們。

下圖展示了在四個通道上的卷積操作，有兩個卷積核，生成兩個通道。其中需要注意的是，四個通道上每個通道對應一個卷積核，先將w2忽略，只看w1，那麼在w1的某位置（i,j）處的值，是由四個通道上（i,j）處的卷積結果相加然後再取啟用函式值得到的。

所以，在上圖由4個通道卷積得到2個通道的過程中，引數的數目為4×2×2×2個，其中4表示4個通道，第一個2表示生成2個通道，最後的2×2表示卷積核大小。

2.4 Down-pooling

在通過卷積獲得了特徵 (features) 之後，下一步我們希望利用這些特徵去做分類。理論上講，人們可以用所有提取得到的特徵去訓練分類器，例如 softmax 分類器，但這樣做面臨計算量的挑戰。例如：對於一個 96X96 畫素的影象，假設我們已經學習得到了400個定義在8X8輸入上的特徵，每一個特徵和影象卷積都會得到一個 (96 − 8 + 1) × (96 − 8 + 1) = 7921 維的卷積特徵，由於有 400 個特徵，所以每個樣例 (example) 都會得到一個 892 × 400 = 3,168,400 維的卷積特徵向量。學習一個擁有超過 3 百萬特徵輸入的分類器十分不便，並且容易出現過擬合 (over-fitting)。

為了解決這個問題，首先回憶一下，我們之所以決定使用卷積後的特徵是因為影象具有一種“靜態性”的屬性，這也就意味著在一個影象區域有用的特徵極有可能在另一個區域同樣適用。因此，為了描述大的影象，一個很自然的想法就是對不同位置的特徵進行聚合統計，例如，人們可以計算影象一個區域上的某個特定特徵的平均值 (或最大值)。這些概要統計特徵不僅具有低得多的維度 (相比使用所有提取得到的特徵)，同時還會改善結果(不容易過擬合)。這種聚合的操作就叫做池化 (pooling)，有時也稱為平均池化或者最大池化 (取決於計算池化的方法)。

至此，卷積神經網路的基本結構和原理已經闡述完畢，下面對常見的卷積神經網路結構進行剖析。

CNN的經典結構始於1998年的LeNet，成於2012年曆史性的AlexNet，從此大盛於影象相關領域，主要包括：
　　1、LeNet，1998年
　　2、AlexNet，2012年
　　3、ZF-net，2013年
　　4、GoogleNet，2014年
　　5、VGG，2014年
　　6、ResNet，2015年

LeNet前面博文已介紹，下面再補充介紹下其它幾種網路結構。

AlexNet

需要注意的是，該模型採用了2-GPU並行結構，即第1、2、4、5卷積層都是將模型引數分為2部分進行訓練的。在這裡，更進一步，並行結構分為資料並行與模型並行。資料並行是指在不同的GPU上，模型結構相同，但將訓練資料進行切分，分別訓練得到不同的模型，然後再將模型進行融合。而模型並行則是，將若干層的模型引數進行切分，不同的GPU上使用相同的資料進行訓練，得到的結果直接連線作為下一層的輸入。

上圖模型的基本引數為：

輸入：224×224大小的圖片，3通道
第一層卷積：5×5大小的卷積核96個，每個GPU上48個。
第一層max-pooling：2×2的核。
第二層卷積：3×3卷積核256個，每個GPU上128個。
第二層max-pooling：2×2的核。
第三層卷積：與上一層是全連線，3*3的卷積核384個。分到兩個GPU上個192個。
第四層卷積：3×3的卷積核384個，兩個GPU各192個。該層與上一層連線沒有經過pooling層。
第五層卷積：3×3的卷積核256個，兩個GPU上個128個。
第五層max-pooling：2×2的核。
第一層全連線：4096維，將第五層max-pooling的輸出連線成為一個一維向量，作為該層的輸入。
第二層全連線：4096維
Softmax層：輸出為1000，輸出的每一維都是圖片屬於該類別的概率。

ZF-Net

【說明】：我想很多人在看faster-rcnn的時候，都會被RPN的網路結構和連線方式糾結，作者在文中說的不是很清晰，這裡給出解析；

【首先】：大家應該要了解卷積神經網路的連線方式，卷積核的維度，反向傳播時是如何靈活的插入一層；這裡我推薦一份資料，真是寫的非常清晰，就是MatConvet的使用者手冊，這個框架底層借用的是caffe的演算法，所以他們的資料結構，網路層的連線方式都是一樣的；建議讀者看看，很快的；

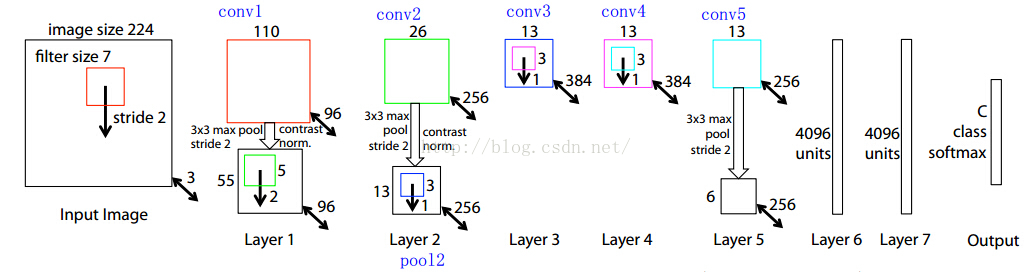
【前面5層】：作者RPN網路前面的5層借用的是ZF網路，這個網路的結構圖我截個圖放在下面，並分析下為什麼是這樣子的，雙向箭頭上的粗體數字是左上側矩形框影象的Channel size，比如3是輸入影象的通道；

首先記住一個公式：卷積後的conv大小=（卷積前conv層寬度-map寬度+填充）/步長+1

1、輸入圖片大小是 224*224*3（這個3是三個通道，也就是RGB三種）；

2、然後第一層的卷積核維度是 7*7*3*96 （所以大家要認識到卷積核都是4維的，在caffe的矩陣計算中都是這麼實現的）；

3、所以conv1得到的結果是110*110*96 （這個110來自於 (224-7+pad)/2 +1 ，這個pad是我們常說的填充，也就是在圖片的周圍補充畫素，這樣做的目的是為了能夠整除，除以2是因為2是圖中的stride， 這個計算方法在上面建議的文件中有說明與推導的）；

4、然後就是做一次池化，得到pool1， 池化的核的大小是3*3，所以池化後圖片的維度是55*55*96  （  (110-3+pad)/2 +1 =55 ）；

5、然後接著就是再一次卷積，這次的卷積核的維度是5*5*96*256 ，得到conv2：26*26*256；

6、後面就是類似的過程了，我就不詳細一步步算了，要注意有些地方除法除不盡，作者是做了填充了，在caffe的prototxt檔案中，可以看到每一層的pad的大小；

7、最後作者取的是conv5的輸出，也就是13*13*256送給RPN網路的；

【RPN部分】：然後，我們看看RPN部分的結構：

1、前面我們指出，這個conv feature map的維度是13*13*256的；

2、作者在文章中指出，sliding window的大小是3*3的，那麼如何得到這個256-d的向量呢？ 這個很簡單了，我們只需要一個3*3*256*256這樣的一個4維的卷積核，就可以將每一個3*3的sliding window 卷積成一個256維的向量；

這裡讀者要注意啊，作者這裡畫的示意圖 僅僅是 針對一個sliding window的；在實際實現中，我們有很多個sliding window，所以得到的並不是一維的256-d向量，實際上還是一個3維的矩陣資料結構；可能寫成for迴圈做sliding window大家會比較清楚，當用矩陣運算的時候，會稍微繞些；

3、然後就是k=9，所以cls layer就是18個輸出節點了，那麼在256-d和cls layer之間使用一個1*1*256*18的卷積核，就可以得到cls layer，當然這個1*1*256*18的卷積核就是大家平常理解的全連線；所以全連線只是卷積操作的一種特殊情況（當卷積核的大小與圖片大小相同的時候，其實所謂的卷積就是全連線了）；

4、reg layer也是一樣了，reg layer的輸出是36個，所以對應的卷積核是1*1*256*36，這樣就可以得到reg layer的輸出了；

5、然後cls layer 和reg layer後面都會接到自己的損失函式上，給出損失函式的值，同時會根據求導的結果，給出反向傳播的資料，這個過程讀者還是參考上面給的文件，寫的挺清楚的；

【作者關於RPN網路的具體定義】：這個作者是放在./models/pascal_voc/ZF/faster_rcnn_alt_opt/stage1_rpn_train.pt 檔案中的；

我把這個檔案拿出來給註釋下：

1. name: "ZF"
2. layer {
3. name: 'input-data' #這一層就是最開始資料輸入
4. type: 'Python'
5. top: 'data' # top表示該層的輸出，所以可以看到這一層輸出三組資料，data，真值框gt_boxes，和相關資訊im_info
6. top: 'im_info' # 這些都是儲存在矩陣中的
7. top: 'gt_boxes'
8. python_param {
9. module: 'roi_data_layer.layer'
10. layer: 'RoIDataLayer'
11. param_str: "'num_classes': 21"
12. }
13. }
14. #========= conv1-conv5 ============
15. layer {
16. name: "conv1"
17. type: "Convolution"
18. bottom: "data" # 輸入data
19. top: "conv1" # 輸出conv1，這裡conv1就代表了這一層輸出資料的名稱，儲存在對應的矩陣中
20. param { lr_mult: 1.0 }
21. param { lr_mult: 2.0 }
22. convolution_param {
23. num_output: 96
24. kernel_size: 7
25. pad: 3 # 這裡可以看到卷積1層 填充了3個畫素
26. stride: 2
27. }
28. }
29. layer {
30. name: "relu1"
31. type: "ReLU"
32. bottom: "conv1"
33. top: "conv1"
34. }
35. layer {
36. name: "norm1"
37. type: "LRN"
38. bottom: "conv1"
39. top: "norm1" # 做歸一化操作，通俗點說就是做個除法
40. lrn_param {
41. local_size: 3
42. alpha: 0.00005
43. beta: 0.75
44. norm_region: WITHIN_CHANNEL
45. engine: CAFFE
46. }
47. }
48. layer {
49. name: "pool1"
50. type: "Pooling"
51. bottom: "norm1"
52. top: "pool1"
53. pooling_param {
54. kernel_size: 3
55. stride: 2
56. pad: 1 # 池化的時候，又做了填充
57. pool: MAX
58. }
59. }
60. layer {
61. name: "conv2"
62. type: "Convolution"
63. bottom: "pool1"
64. top: "conv2"
65. param { lr_mult: 1.0 }
66. param { lr_mult: 2.0 }
67. convolution_param {
68. num_output: 256
69. kernel_size: 5
70. pad: 2
71. stride: 2
72. }
73. }
74. layer {
75. name: "relu2"
76. type: "ReLU"
77. bottom: "conv2"
78. top: "conv2"
79. }
80. layer {
81. name: "norm2"
82. type: "LRN"
83. bottom: "conv2"
84. top: "norm2"
85. lrn_param {
86. local_size: 3
87. alpha: 0.00005
88. beta: 0.75
89. norm_region: WITHIN_CHANNEL
90. engine: CAFFE
91. }
92. }
93. layer {
94. name: "pool2"
95. type: "Pooling"
96. bottom: "norm2"
97. top: "pool2"
98. pooling_param {
99. kernel_size: 3
100. stride: 2
101. pad: 1
102. pool: MAX
103. }
104. }
105. layer {
106. name: "conv3"
107. type: "Convolution"
108. bottom: "pool2"
109. top: "conv3"
110. param { lr_mult: 1.0 }
111. param { lr_mult: 2.0 }
112. convolution_param {
113. num_output: 384
114. kernel_size: 3
115. pad: 1
116. stride: 1
117. }
118. }
119. layer {
120. name: "relu3"
121. type: "ReLU"
122. bottom: "conv3"
123. top: "conv3"
124. }
125. layer {
126. name: "conv4"
127. type: "Convolution"
128. bottom: "conv3"
129. top: "conv4"
130. param { lr_mult: 1.0 }
131. param { lr_mult: 2.0 }
132. convolution_param {
133. num_output: 384
134. kernel_size: 3
135. pad: 1
136. stride: 1
137. }
138. }
139. layer {
140. name: "relu4"
141. type: "ReLU"
142. bottom: "conv4"
143. top: "conv4"
144. }
145. layer {
146. name: "conv5"
147. type: "Convolution"
148. bottom: "conv4"
149. top: "conv5"
150. param { lr_mult: 1.0 }
151. param { lr_mult: 2.0 }
152. convolution_param {
153. num_output: 256
154. kernel_size: 3
155. pad: 1
156. stride: 1
157. }
158. }
159. layer {
160. name: "relu5"
161. type: "ReLU"
162. bottom: "conv5"
163. top: "conv5"
164. }
165. #========= RPN ============
166. # 到我們的RPN網路部分了，前面的都是共享的5層卷積層的部分
167. layer {
168. name: "rpn_conv1"
169. type: "Convolution"
170. bottom: "conv5"
171. top: "rpn_conv1"
172. param { lr_mult: 1.0 }
173. param { lr_mult: 2.0 }
174. convolution_param {
175. num_output: 256
176. kernel_size: 3 pad: 1 stride: 1 #這裡作者把每個滑窗3*3，通過3*3*256*256的卷積核輸出256維，完整的輸出其實是12*12*256,
177. weight_filler { type: "gaussian" std: 0.01 }
178. bias_filler { type: "constant" value: 0 }
179. }
180. }
181. layer {
182. name: "rpn_relu1"
183. type: "ReLU"
184. bottom: "rpn_conv1"
185. top: "rpn_conv1"
186. }
187. layer {
188. name: "rpn_cls_score"
189. type: "Convolution"
190. bottom: "rpn_conv1"
191. top: "rpn_cls_score"
192. param { lr_mult: 1.0 }
193. param { lr_mult: 2.0 }
194. convolution_param {
195. num_output: 18 # 2(bg/fg) * 9(anchors)
196. kernel_size: 1 pad: 0 stride: 1 #這裡看的很清楚，作者通過1*1*256*18的卷積核，將前面的256維資料轉換成了18個輸出
197. weight_filler { type: "gaussian" std: 0.01 }
198. bias_filler { type: "constant" value: 0 }
199. }
200. }
201. layer {
202. name: "rpn_bbox_pred"
203. type: "Convolution"
204. bottom: "rpn_conv1"
205. top: "rpn_bbox_pred"
206. param { lr_mult: 1.0 }
207. param { lr_mult: 2.0 }
208. convolution_param {
209. num_output: 36 # 4 * 9(anchors)
210. kernel_size: 1 pad: 0 stride: 1 <span style="font-family: Arial, Helvetica, sans-serif;">#這裡看的很清楚，作者通過1*1*256*36的卷積核，將前面的256維資料轉換成了36個輸出</span>
211. weight_filler { type: "gaussian" std: 0.01 }
212. bias_filler {
     相關推薦

     常用卷積神經網路從基本原理到結構彙總

     先明確一點就是，Deep Learning是全部深度學習演算法的總稱，CNN是深度學習演算法在影象處理領域的一個應用。第一點，在學習Deep learning和CNN之前，總以為它們是很了不得的知識，總以為它們能解決很多問題，學習了之後，才知道它們不過與其他機器學習演算法如s

     《TensorFlow：實戰Google深度學習框架》——6.2 卷積神經網路簡介（卷積神經網路的基本網路結構及其與全連線神經網路的差異）

     下圖為全連線神經網路與卷積神經網路的結構對比圖： 由上圖來分析兩者的差異：                  全連線神經網路與卷積網路相同點   &nb

     萬字長文|如何直觀解釋卷積神經網路的工作原理？

     作者：YJango 日本會津大學|人機互動實驗室博士生 量子位 已獲授權編輯釋出 該文是對卷積神經網路的介紹，並假設你理解前饋神經網路。 如果不是，強烈建議讀完《如何簡單形象又有趣地講解神經網路是什麼？》這篇文章後後再來讀該篇。 推薦文章連結： https://www.zhihu.com/ques

     【深度學習】卷積神經網路CNN基本知識點

     卷積神經網路與前面學的常規神經網路很相似，也有輸入、權重、偏差、損失函式、啟用函式、全連線層等概念，之前的一些小的技巧也仍然適用。 與常規神經網路的對比 卷積神經網路（Convolutional Neural Networks，CNNs / ConvNe

     深度學習筆記五：卷積神經網路CNN(基本理論)

     一.初識卷積網路結構 Ⅰ.概覽 前面已經做過手寫體識別的任務。之前我們只是使用了兩層的全連線層，或者根據喜好多加幾層。我更喜歡把這樣的結構叫做多層感知機，即使用到了一些現代的權重初始化方式，更好的啟用函式reLU等，我還是傾向於叫做多層感知機。

     【Deep learning】卷積神經網路CNN演算法原理

     寫在前面在上一篇【Deep learning】卷積神經網路CNN結構中我們簡單地介紹了CNN的結構。接下來我們看看這種結構的CNN模型是怎麼執行的，包括CNN的前向傳播和反向傳播演算法。1.CNN前向傳播演算法（1）輸入層前向傳播到卷積層輸入層的前向傳播是CNN前向傳播演算法

     卷積神經網路從lenet到DPN發展歷程

     先發一張圖（不全），以後再補一，LeNet51998， Yann LeCun 的 LeNet5。最早的卷積網路，已經有了卷積層，池化層和全連線層。二，AlexNet2012，ImageNet Classification with DeepConvolutional Neur

     經典的幾個卷積神經網路（基本網路）

     AlexNet： （ 2012 ILSVRC top 5 test error rate of 15.4%） 第一個成功展現出卷積神經網路潛力的網路結構。 關鍵點： 通過大量的資料與長時間的訓練得到最後的模型，結果十分顯著（拿到2012分類

     CNN--卷積神經網路從R-CNN到Faster R-CNN的理解(CIFAR10分類程式碼)

     1. 什麼是CNN 卷積神經網路（Convolutional Neural Networks, CNN）是一類包含卷積計算且具有深度結構的前饋神經網路（Feedforward Neural Networks），是深度學習（deep learning）的代表演算法之一。 我們先來看卷積神經網路各個層級結構圖

     乾貨 | 深度學習之卷積神經網路(CNN)的模型結構

     微信公眾號 關鍵字全網搜尋最新排名 【機器學習演算法】：排名第一 【機器學習】：排名第一 【Python】：排名第三 【演算法】：排名第四 前言 在前面我們講述了DNN的模型與前向反向傳播演算法。而在DNN大類中，卷積神經網路(Convolutional Neural Networks，以下簡稱CNN)是最

     【深度學習系列】卷積神經網路CNN原理詳解(一)——基本原理

     轉自：https://www.cnblogs.com/charlotte77/p/7759802.html 上篇文章我們給出了用paddlepaddle來做手寫數字識別的示例，並對網路結構進行到了調整，提高了識別的精度。有的同學表示不是很理解原理，為什麼傳統的機

     深入理解卷積神經網路(CNN)——從原理到實現

     王琦      QQ：451165431      計算機視覺&深度學習 本篇通過在MNIST上的實驗，引出卷積神經網路相關問題，詳細闡釋其原理以及常用技巧、調參方法。歡迎討論相關技術&學術問題，但謝絕拿來主義。 程式碼是博主自己

     卷積神經網路（CNN）一之概念原理

     　　什麼是卷積神經網路呢？這個的確是比較難搞懂的概念，特別是一聽到神經網路，大家腦海中第一個就會想到複雜的生物學，讓人不寒而慄，那麼複雜啊．卷積神經網路是做什麼用的呢？它到底是一個什麼東東呢？ 卷積神經網路的靈感源一種生物程序，其中神經元之間的聯結模式和動物視覺皮層組織非常相似。所以發明者把它叫做卷積神經網

     tensorflow基本教程8：手寫體分類卷積神經網路

     import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data #number 1 to 10 data mnist=input_data.read_data_sets('MNIST_data'

     DeepLearning tutorial（4）CNN卷積神經網路原理簡介+程式碼詳解

     分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

     淺談卷積神經網路CNN原理

     做手寫數字識別時，對網路結構進行到了調整，提高了識別的精度。傳統的機器學習演算法，簡單的神經網路(如多層感知機)都可以識別手寫數字，我們要採用卷積神經網路CNN來進行別呢？CNN到底是怎麼識別的？用CNN有哪些優勢呢？我下面就來簡單分析一下。 為什麼要用神經網路？ 對於同一個分類任務，我

     深度學習、影象識別入門，從VGG16卷積神經網路開始

     剛開始接觸深度學習、卷積神經網路的時候非常懵逼，不知道從何入手，我覺得應該有一個進階的過程，也就是說，理應有一些基本概念作為奠基石，讓你有底氣去完全理解一個龐大的卷積神經網路： 本文思路： 一、我認為學習卷積神經網路必須知道的幾個概念： 1、卷積過程： 我們經常說卷積神經網路卷積神經網路，到

     《TensorFlow：實戰Google深度學習框架》——6.3 卷積神經網路常用結構

     1、卷積層 圖6-8顯示了卷積層神經網路結構中重要的部分：濾波器（filter）或者核心（kernel）。 過濾器可以將當前層神經網路上的一個子節點矩陣轉化為下一層神經網路上的一個單位節點矩陣 。 單位節點矩陣指的是一個長和寬都為1，但深度不限的節點矩陣 。 在一個卷積層巾，過濾器

     《TensorFlow：實戰Google深度學習框架》——6.3 卷積神經網路常用結構（池化層）

     池化層在兩個卷積層之間，可以有效的縮小矩陣的尺寸（也可以減小矩陣深度，但實踐中一般不會這樣使用），co。池從而減少最後全連線層中的引數。 池化層既可以加快計算速度也可以防止過度擬合問題的作用。 池化層也是通過一個類似過濾器結構完成的，計算方式有兩種： 最大池化層：採用最

     Tensorflow 入門學習13.卷積神經網路原理3.（網路結構詳解）

     本文學習內容來自《TensorFlow深度學習應用實踐》 從前面介紹的卷積運算的基本原理和概念，從本質上來說卷積神經網路就是將影象處理的二維離散卷積運算和神經網路相結合。這種卷積運算可以用於自動提取特徵，而卷積神經網路也主要應用於二維影象的識別。 卷積神經網路原