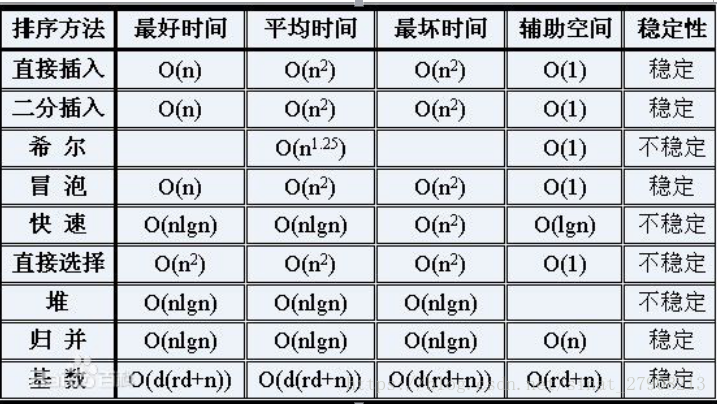
三個簡單排序演算法:氣泡排序、選擇排序、插入排序
以下從基礎開始,逐步詳細複習各個排序演算法。先從三個最基礎最簡單的排序演算法開始。他們分別是氣泡排序、選擇排序、插入排序。以下都是java程式碼,並且認為升序是有序。
一、氣泡排序
1、程式碼
public class Main{//氣泡排序 public static void main(String[] args){ int[] a=new int[]{1,3,1,2,0,4,5,2,6,2,0}; int n=a.length; boolean flag=true;//如果對於一趟比較,沒有交換的動作,也就是已經有序了,就直接結束排序,不需要進行後面的比較了 for(int i=n-1;i>0;i--){//第一層迴圈從n-1到1 flag=true; for(int j=0;j<i;j++)//第二層迴圈從0到n-1 if(a[j]>a[j+1]){//如果遇到不符合順序的資料就交換他們 swap(a, j, j+1); flag=false; } if(flag==true) break; } print(a); } public static void swap(int[] a,int i,int j){ int temp=a[i]; a[i]=a[j]; a[j]=temp; } public static void print(int[] a){ int n=a.length; for(int i=0;i<n;i++) System.out.print(a[i]+" "); } }
2、時間和空間複雜度分析
(1)最好時間複雜度
如果檔案初始狀態剛好是正序的,一趟掃描便可以完成排序。這個時候只需要掃描n-1次,交換0次。因此最好的時間複雜度為O(n)。而做到這個最好時間複雜度的前提是有flag這個變數的存在,他可以判斷是否序列已經有序了。
(2)最差時間複雜度
最壞的情況是如果序列是逆序的,那需要進行n-1次迴圈,每次迴圈需要進行n-i次比較(1<=i<=n),並且每次比較都需要移動三次記錄來交換記錄的位置。交換操作比比較事實上耗費更多的時間。因此需要比較n(n-1)/2次,交換3n(n-1)/2次。因此最壞的時間複雜度是O(n^2)。事實上,我們可以把交換的三步當做一步的交換操作,所以也可以認為是交換n(n-1)/2次。後面我們都這樣分析,這樣比較簡便。
(3)平均時間複雜度
平均來說,是O(n^2)。
(4)空間複雜度
不需要用到額外的很多空間,因此空間複雜度是O(1)。
3、演算法穩定性
氣泡排序就是把小的元素往前調或者把大的元素往後調。比較是相鄰的兩個元素比較,交換也發生在這兩個元素之間。所以,如果兩個元素相等,我想你是不會再無聊地把他們倆交換一下的;如果兩個相等的元素沒有相鄰,那麼即使通過前面的兩兩交換把兩個相鄰起來,這時候也不會交換,所以相同元素的前後順序並沒有改變,所以氣泡排序是一種穩定排序演算法。
二、選擇排序
選擇排序,顧名思義就是每一次從待排序的資料元素中選出最小的一個元素,存放在序列的起始位置,直到全部待排序的資料元素排完。
1、程式碼
public class Main{//選擇排序 public static void main(String[] args){ int[] a=new int[]{1,3,1,2,0,4,5,2,6,2,0}; int n=a.length; int min;//記錄最小那個數的下標 for(int i=0;i<n-1;i++){ min=i; for(int j=i+1;j<n;j++) if(a[j]<a[min]) min=j; swap(a, i, min); } print(a); } public static void swap(int[] a,int i,int j){ int temp=a[i]; a[i]=a[j]; a[j]=temp; } public static void print(int[] a){ int n=a.length; for(int i=0;i<n;i++) System.out.print(a[i]+" "); } }
2、時間和空間複雜度分析
(1)最好時間複雜度
最好的情況下是序列本身已經有序。但是就算序列本身有序,演算法也需要進行(n-1)+(n-2)+...+1=n*(n-1)/2次比較(無論有序還是無序,都是進行這麼多次比較),但是隻需要交換0次。所以最好時間複雜度是O(n^2)。
(2)最壞時間複雜度
最壞的情況,也只需要交換n-1次。最壞時間複雜度是O(n^2)。
(3)平均時間複雜度
O(n^2)。
(4)空間複雜度
只需要一個額外的輔助儲存空間,因此是O(1)。
3、穩定性
選擇排序是給每個位置選擇當前元素最小的,比如給第一個位置選擇最小的,在剩餘元素裡面給第二個元素選擇第二小的,依次類推,直到第n-1個元素,第n個元素不用選擇了,因為只剩下它一個最大的元素了。那麼,在一趟選擇,如果一個元素比當前元素小,而該小的元素又出現在一個和當前元素相等的元素後面,那麼交換後穩定性就被破壞了。比較拗口,舉個例子,序列5 8 5 2 9,我們知道第一遍選擇第1個元素5會和2交換,那麼原序列中兩個5的相對前後順序就被破壞了,所以選擇排序是一個不穩定的排序演算法。
4、與其他演算法比較
可以看到,交換次數比氣泡排序少多了,由於交換所需CPU時間比比較所需的CPU時間多,n值較小時,選擇排序比氣泡排序快。
三、插入排序
插入排序的基本操作就是將一個數據按值大小插入到已經排好序的有序資料中,從而得到一個新的、個數加一的有序資料。當然,這個有序陣列一開始就是要排序的那個陣列的開始第一個數。
1、程式碼
public class Main{//插入排序
public static void main(String[] args){
int[] a=new int[]{1,3,1,2,0,4,5,2,6,2,0};
int n=a.length;
int i,j,temp;//用來暫存
for(i=1;i<n;i++){
temp=a[i];
j=i-1;
for(;j>=0&&a[j]>temp;j--)//找到插入位置的同時往一邊整體移動陣列
a[j+1]=a[j];
if(j!=i-1)//j等於i-1的話自然不需要填補了
a[j+1]=temp;
}
print(a);
}
public static void print(int[] a){
int n=a.length;
for(int i=0;i<n;i++)
System.out.print(a[i]+" ");
}
}2、時間和空間複雜度
(1)最好時間複雜度
最好的情況是已經升序了,這樣的話只需要進行n-1次比較操作就可以了,因此是O(n)。
(2)最壞時間複雜度
最壞的情況是降序,這樣要進行n(n-1)/2次比較和n(n-1)/2+n-1次賦值操作,因此是O(n^2)。
(3)平均時間複雜度
O(n^2)。
(4)空間複雜度
O(1)。
3、穩定性
插入排序是在一個已經有序的小序列的基礎上,一次插入一個元素。當然,剛開始這個有序的小序列只有1個元素,就是第一個元素。比較是從有序序列的末尾開始,也就是想要插入的元素和已經有序的最大者開始比起,如果比它大則直接插入在其後面,否則一直往前找直到找到它該插入的位置。如果碰見一個和插入元素相等的,那麼插入元素把想插入的元素放在相等元素的後面。所以,相等元素的前後順序沒有改變,從原無序序列出去的順序就是排好序後的順序,所以插入排序是穩定的。
4、適用性
當陣列基本有序的情況下適合使用插入排序和氣泡排序,它們在基本有序的情況下排序的時間複雜度接近O(n)。當n比較小的時候,適合插入排序和選擇排序,如果元素包含的內容過大,就不適合插入排序,因為插入排序需要移動元素的次數比較多。