詞法分析:從RE(正則表示式)到DFA(確定的有限狀態機)
模式識別(Pattern recognization)是現在非常流行的一個詞,我們對詞法的分析也是基於模式(pattern-based)的。我們用正則表示式(Regular Expression)來定義單詞的模式,而在詞法分析時,有限狀態機(Finite Automata)更便於我們分析。本文介紹將正則表示式(RE)轉為確定的有限狀態機(DFA)的方法。
首先,什麼是確定的有限狀態機,什麼是非確定的有限狀態機(NFA)?用通俗的語言講,在面對相同的輸入引數時,NFA可能會跳轉到多種狀態,而DFA只會跳轉到特定的狀態,有DFA類似於函式,而NFA類似一對多的對映。
DFA用程式可以描述為:
state = 1 從上面的程式碼段,我們需要知道:
- DFA=>program:從確定的有限狀態機可以生成確定的程式
- Each state=>a fragment of code:每個狀態對應一個case。
- Each edge=>a judgement:每條邊對應一個if判斷
從RE推出DFA的步驟:RE=>NFA=>DFA=optimization=>DFAo=>program
1. 從RE到NFA
從正則表示式到非確定的有限狀態機對於人來說非常好理解,但是對於機器來說確比較複雜。從RE到DFA有兩種方法:自頂向下逐步分解法和自下而上組合方法(Thompson方法)。
自頂向下逐步分解法:Top-down stepwise refinement according to the structure of RE
這種方法符合人的思維習慣,首先我們從最簡單的情況開始考慮。
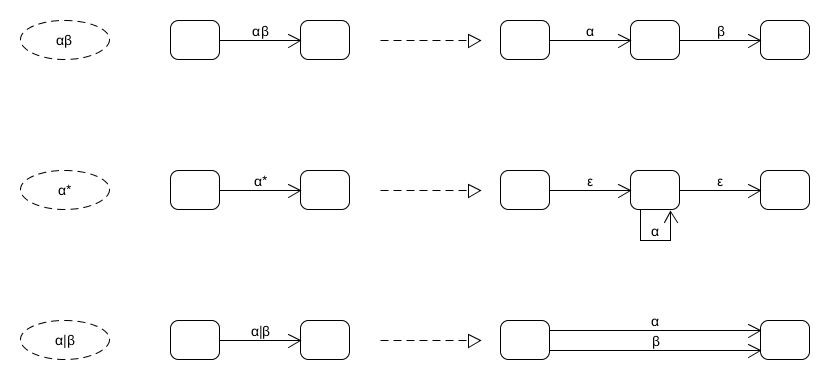
以(a|b)* a (a|b) (a|b)為例,這個正則表示式符合上面的αβ特徵,因此第一步可以變成:

而對於(a|b)*,又符合上面的a*特徵,因此(a|b)*可以繼續分解為
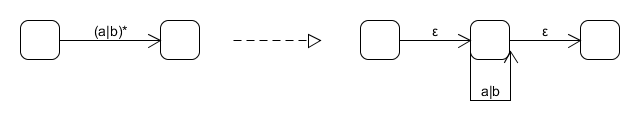
可以看到a|b還可以繼續分解,類似這樣的分解過程到所有邊的標記只剩下ε或字母表的單一字元為止。
然而,對於計算機來說,字元是一個一個讀入的,計算機不能從整體把握情況逐步向下分解,因此我們還需要適合計算機的方法。
自下而上組合法:Bottom-up combination(Thomson方法)
這種比前一種方法稍微複雜一點,但其實想法也很簡單,我試著換一種表述來解釋這個方法。
在遇到單個的字元時,我們直接構造轉換圖,比如遇到a時,我們就構造這樣的轉換圖:
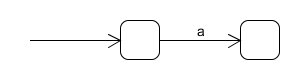
這樣,我們就形成了一個單元U,這個U就是上面已經生成的轉換圖。
在遇到操作符時,我們所有的處理都是針對單元的,在下面的圖示中,我們用虛線圓圈表示一個單元。
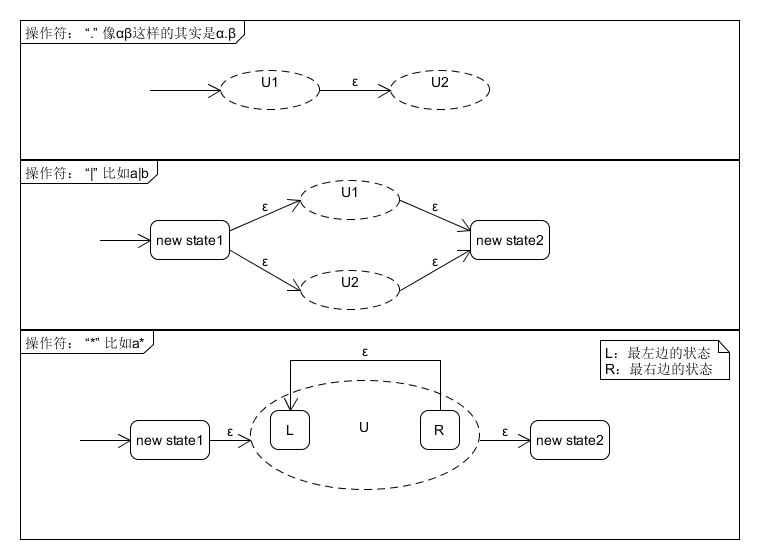
在處理完操作符後形成的仍是一個單元,處理完後的整體變成單元U’參與下一次處理。這裡類似於一種遞迴的過程。
但是,像a|b這樣的式子,在處理‘|’這個操作符時,我們顯然需要兩個單元,但計算機在讀到‘|’操作符時,我們在為a構造了轉換圖,計算機還不知道b的存在,也就不能做上面這樣的處理,所以這種方法需要以下條件:
- 正則表示式(RE)需要處理為字尾表示式
- 正則表示式(RE)中需要寫明操作符‘.’,如ab需要寫為a.b
滿足以上條件後,計算機可以用這種方法自動生成NFA。
2. 從NFA到DFA
對於一個已經形成的NFA,我們需要定義新的狀態來形成DFA。首先要解釋兩種方法和他們對應的使用情形。
NFA之所以為NFA而不是DFA,主要是因為以下兩個原因,解決以下的兩種情形,就能將NFA轉為DFA。
邊上的ε:ε閉包
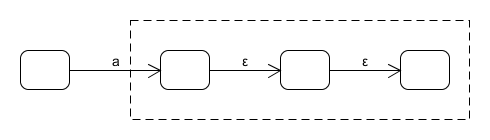
遇到這種情況,後面的三個狀態完全可以合併,如果將後面的三個狀態合為一個,那這個轉換圖裡就沒有ε邊,也就滿足了DFA的條件。
對應的解決方法是找出ε閉包,也就是先找出該狀態的ε邊推出的所有狀態,再找那些狀態的ε邊推出的狀態,是一個迭代的過程,直到找出一個狀態的ε閉包。如果是從狀態x開始的,我們將通過該過程找到的所有狀態集稱為以x狀態為核的ε閉包,記為ε-closure({x}),或ε-c({x})。從定義可以知道,核相同,推出的ε閉包一定相同。
不確定的後續狀態:子集構造法
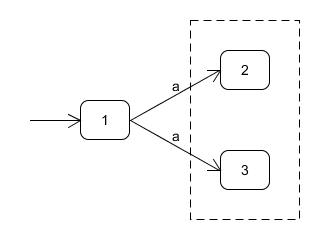
遇到這種情況,如果能將狀態2和狀態3合併到一起,就不會出現“面對相同的輸入狀態可能跳轉到多種狀態的情形了”,合併狀態2和狀態3這樣類似的狀態的方法叫做子集構造法,若從狀態Ii開始,以a邊推出的所有狀態集合為B,我們記為Ii–a–>B,比如上圖可以記為1-a->{2,3}
綜合使用:表驅動法
上面只是簡單介紹了兩種情形,說明了從NFA轉化到DFA的重點是重新組合NFA狀態。下面我們討論系統的可程式設計的過程來將NFA轉化為DFA,運用的還是上面的兩種方法,我們需要構建一張表來展示構建的DFA裡的所有狀態。
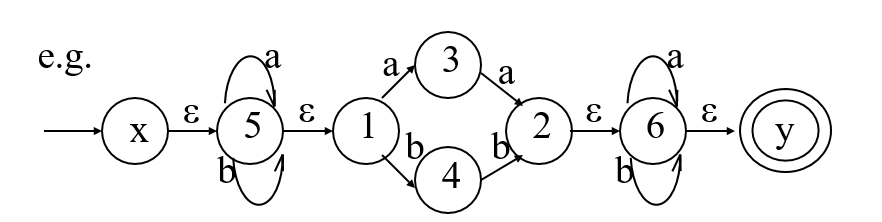
以下圖中的NFA為例:
| DFA State Ii (這裡是新生成的DFA裡的狀態) | a(這個狀態從a邊推出什麼狀態) | b (這個狀態從b邊推出什麼狀態) |
|---|---|---|
| I0=ε-c({x})={x,5,1} | ε-c(I0-a->{5,3})={5,3,1}=I1 | ε-c(I1-b->{5,4})={5,4,1}=I2 |
| I1={5,3,1} | … | … |
| I2={5,4,1} | … | … |
解釋:首先從起點x開始構造新的DFA裡的第一個狀態I0,也就是尋找以x為核的ε閉包ε-c({x}),然後構造新的I0從a、b邊推出的狀態,方法是先使用子集構造法,再尋找構造後的子集的ε閉包。這樣我們就找到了新的狀態I1,I2,第二行、第三行就是尋找I1,I2以a、b邊推出的狀態,這樣就能找到更多的狀態,當沒有新的狀態產生時,這樣的過程終止。這類似於一種迭代的過程。
這題最終的結果是:
3. 從DFA到DFAo(DFA優化)
在上面生成的DFA中,每個狀態都有以a、b推出的狀態,有時候這可能意味著多餘。DFA優化(Optimization of a DFA)的思想是減少DFA中的狀態,我們用到離散數學中等價類劃分的思想,如果兩個狀態等價,那麼他們屬於同一個等價類,我們只需要選擇其中的一個代表即可。
如何劃分等價類呢?
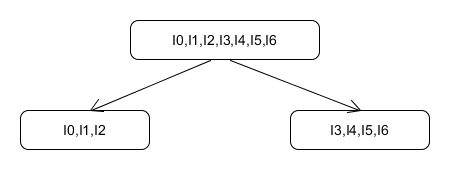
1)找出終止狀態
什麼樣的狀態可以被稱為終止狀態呢?在上例的NFA圖中,y狀態為終止狀態。我們要做的是在I0~I6中找出終止狀態。我們這樣定義新的DFA中的終止狀態:若Ii
因此第一步我們將上面的狀態分為兩類:終止狀態和非終止狀態。
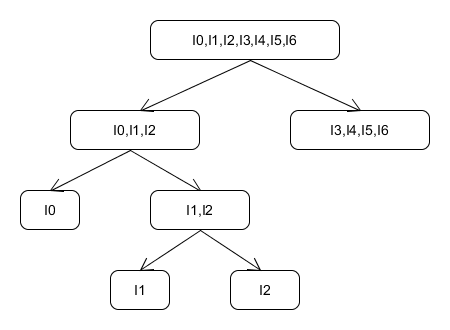
2)劃分等價類
第一步已經將狀態分為了兩類,下面我們要繼續拆分。我們規定這樣的這樣的狀態Ii,Ij屬於同一個等價類:
- Ii,Ij發出的邊數相同。
- Ii,Ij發出的邊相同。
- 對應相同的邊連線的狀態屬於同一個等價類。
如I0和I1,他們對應的a邊發出的狀態分別是I1和I3,而在第一步中這兩個狀態已經被劃分到了兩類裡,一定不是等價的,所以我們將I0,I1拆分,也就是將I0單獨分出去。
3)回頭看
在劃分完後面的等價類時,我們還要回頭看一下前面的等價類還可不可以劃分。有時候前面在比較時後面的類還沒有劃分,因此判斷屬於同一個等價類不拆分,而到後面等價類判斷時拆分了這個等價類,前面判斷的兩個狀態可以就到了不同的等價類裡,這就需要我們回頭檢查是不是所有的類都不能再拆分了。
4)選取代表
分好等價類後每個類選取一個狀態作為代表,這個類的其他狀態都用這個代表代替,重新構造DFA轉化圖。
這樣,我們就將RE轉換成優化後的DFA,儘管過程比較複雜,但是這樣機械而固定的過程是可以程式設計解決的。在構造完DFA後,我們可以開始做更多的詞法分析工作。