dijkstra求最短路徑長度
阿新 • • 發佈:2019-02-12
概述
dijkstra演算法是單源最短路徑演算法的一種。
所謂單源,即在一個有向圖中,從一個節點出發,演算法可求該節點至所有可到達節點的最短路徑長度。與之相對的稱為非單源最短路,即演算法執行一次可求出任意節點至任意可到達節點的最短路長度,其代表是floyd演算法。單源最短路有兩種常見演算法,dijkstra演算法和bellman-ford演算法。前者只能用於求路徑權值全部為非負數的最短路,但後者是可以求邊權中出現負數的演算法。既然非單源一次可以求出任意節點間的最短路,我們為什麼還要使用單源演算法呢?
因為floyd的時間複雜度為O(n^3),而dijkstra只有O(n^2)。如果要求出任意節點間的最短路,那麼兩個演算法似乎都是O(n^3),然而floyd似乎更好理解。
dijkstra演算法描述:
設G=(V,E)是一個有向圖,V表示頂點,E表示邊;它的每一條邊(i,j)屬於E,都有一個非負權W(i,j);在G中指定一個結點V0,要求求出從V0到G的每一個節點Vj(Vj屬於V)的最短路徑長度。
舉例
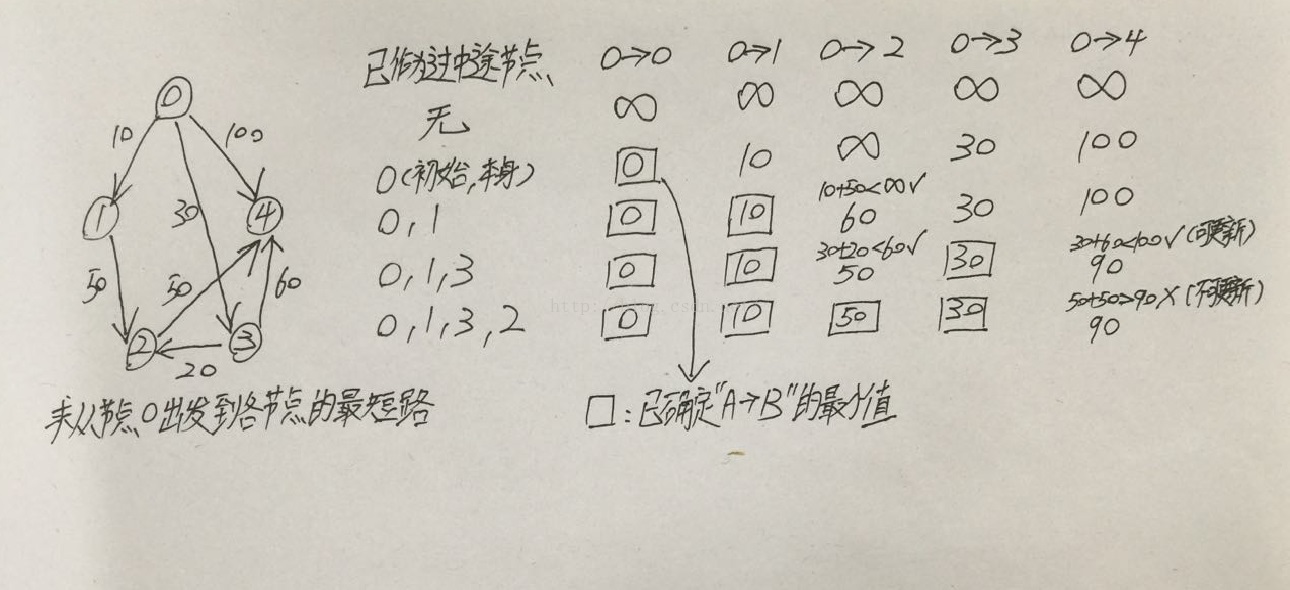
根據下圖,求從節點0開始到各節點的最短距離:
配合圖中右邊的過程:
- 首先我們先將從節點0出發的所有路徑長度標記為無窮大。
- 由於從節點0出發,故更新從節點0到其直接相鄰節點的路徑長度,0->1:10,0->3:30,0->4:100。
- 取出其中最小的0->1:10,並且我們已經清楚0->1的距離已經是最短的了。
解釋:從0到1無非兩種走法,0直接到達1或0通過其他節點到達1。現在0到1的距離為10,其已小於0到其餘節點的距離,即0->C->1=(30或100)+C->1,0->C->1已經不可能小於現在的0->1了,故現在的0->1已經是最短的,不可能有更短的0->1。
接著我們看下從節點1到其餘節點的路徑,明顯有一條1->2:50,通過1->2可以產生0->1->2:60這條路徑,該路徑長度遠小於現在表裡的0->2為無窮大,故更新0->2:60。 - 接下來取出表裡最小且沒有使用過的值,0->3:30。同理,從節點3到節點2、4有直接的路徑,得出0->3->2:50,其小於表中的0->2:60,故更新;0->3->4:90,其小於表中的0->4:100,故更新。
- 到此時,0->1:10,0->2:50,0->3:30,0->4:90,其中節點0、1、3已經被使用過,所以下面我們取出表裡的最小且沒有使用過的值,0->2:50。同理,節點2到4有一條直接路徑,0->2->4:100,但其大於表中的0->4:90,故不更新。
演算法步驟
步驟一:初始路徑長度均為無窮大,將出發節點作為節點B和A。
步驟二:找到A節點射出的路徑,將A節點作為中途節點,C為任意節點。當B->A->C<B->C,更新表中B->C的長度。
步驟三:從表中選出最小且未作為過A節點的值,將其對應的節點作為A;重複步驟二,直至所有節點均被作為過A節點。
程式碼實現
根據上圖的例子,給出對應的演算法,求解從節點0到各節點的最短路長度:
#include<stdio.h>
const int N=100;
const int INF=100000; //INF假定為無窮大
int p[N][N],d[N]; //p表示各節點間的距離,不存在路徑即為無窮大;d表示從出發節點到各節點的最短路徑長度
void dijkstra(int sec,int n) //sec為出發節點,n為圖中的節點數
{
int i,j,min,min_num;
int vis[N]={0,}; //用於標記是否已作為過中途節點,0表示沒有,1表示有
for(i=0;i<n;i++) //初始化
{
d[i]=p[sec][i];
}
vis[sec]=1;d[sec]=0; //出發節點到自己的距離永遠為0
for(i=1;i<n;i++)
{
min=INF;
for(j=0;j<n;j++) //每次迴圈取出d陣列中的未被作為過中途節點且數值最小的
{
if(!vis[j]&&d[j]<min)
{
min=d[j]; //更新最小值
min_num=j; //更新最小值所對應的節點,即記錄下標
}
}
vis[min_num]=1; //標記該節點,表示其已被作為中途節點
for(j=0;j<n;j++) //迴圈,經過min_num節點到達是否有更小距離,如有更小距離則更新d陣列
{
if(d[j]>min+p[min_num][j])
{
d[j]=min+p[min_num][j];
}
}
}
}
int main()
{
int i,j,n=5; //n表示圖中的節點個數
for(i=0;i<n;i++) //程式用二維陣列p儲存各節點間的距離,這裡則進行初始化
{
for(j=0;j<n;j++)
{
p[i][j]=(i==j?0:INF); //初始化:i到j路徑為無窮大或者i到i本身為0
}
}
p[0][1]=10;p[0][3]=30;p[0][4]=100;p[1][2]=50;p[2][4]=50;p[3][2]=20;p[3][4]=60; //p[i][j]表示節點i到節點j的距離
dijkstra(0,n); //求從節點0出發到各節點的最短距離
for(i=0;i<n;i++) //列印從節點0出發到各節點的最短距離
{
printf(i==n-1?"%d\n":"%d ",d[i]);
}
return 0;
}記錄路徑
如何在求最短路長度的同時記錄路徑呢?可以看這篇部落格“dijkstra求最短路並記錄路徑”