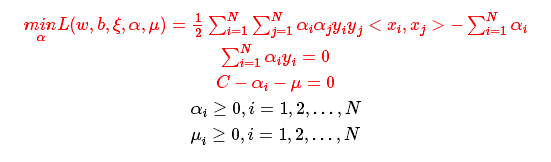2. 程式人生 > >支援向量機之非線性支援向量機（四）

支援向量機之非線性支援向量機（四）

阿新 • • 發佈：2019-02-13

非線性支援向量機與核函式

核技巧

對於非線性分類問題，可以轉換成線性問題求解。
首先，將原始特徵空間資料對映到新的空間
然後，在新的空間利用線性可分支援向量機方法求解

核函式

設X是輸入空間，設H是特徵空間，如果存在一個從X−>H的對映:ϕ(x):X−>H
使得對所有的x,zϵX，核函式滿足：


K(x,z)=ϕ(x)∗ϕ(z)

則稱K(x,z)是核函式，ϕ(x)為對映函式，ϕ(x)∗ϕ(z)為內積

在學習中一般情況核函式有自己定義輸入的。

核函式應用到支援向量機

線性支援向量機的對偶問題是：

這裡寫圖片描述

換成核函式只需要將上面的<xi

,xj>的內積換成K(xi,xj)

目標函式是：


w(α)=12∑Ni=1∑Nj=1αiαjK(xi,xj)−∑Ni=1αi

分類決策函式是：


f(x)=sign(∑Ni=1α∗iyiK(xi,x))+b∗

常用到的核函式

1.多項式核函式（polynomial kernel function）


K(x,z)=(a∗x∗z+b)p

a,b,p是常數，p一般取3，有個理論是：三次函式可以擬合出任意形式的函式。
2.高斯核函式(Gaussian kernel function)

K(x,z)=exp(−||x−z||22σ2)

σ也是自己輸入的
對應的支援向量機是高斯徑向基函式（radial basis function，簡稱RBF）分類器

這兩個比較常見的

非線性支援向量機分類器

最優化問題：
目標函式是：


minα12∑Ni=1∑Nj=1αiαjK(xi,xj)−∑Ni=1αi
s.t.∑Ni=1αiyi=0
0<=αi<=C,i=1,2,...,N

最優解：

α∗=(α∗1,α∗2,...,α∗N)

選擇α∗的一個正分量0<α∗j<C


b∗=<

相關推薦

支援向量機之非線性支援向量機（四）

非線性支援向量機與核函式 核技巧 對於非線性分類問題，可以轉換成線性問題求解。 首先，將原始特徵空間資料對映到新的空間 然後，在新的空間利用線性可分支援向量機方法求解 核函式 設X是輸入空間，設H是特徵空間，如果存在一個從X−>H的

支援資原始檔替換的多渠道打包外掛（四）

一、寫在前面 經過前面幾篇文章的學習（什麼？你還沒看，趕緊去補補！），對gradle已經有了大致的瞭解了，當學習完後一定需要碼程式碼來鞏固一下，所謂：talk is cheap show me the code！今天就帶大家來一場gradle實戰，

UI組件之AdapterView及其子類（四）Gallery畫廊控件使用

convert cal instance ram scaletype 循環 reat targe 外觀 聽說 Gallery如今已經不使用了，API使用ViewPaper取代了，以後再學專研ViewPaper吧如今說說Gallery畫廊，就是不停顯示圖片的意思 Gall

MVC之排球比賽計分程序 ——（四）視圖的設計與實現

元素 role view logs image 技術 size 之前 log （view）視圖 視圖是用戶看到並與之交互的界面。對老式的Web應用程序來說，視圖就是由HTML元素組成的界面，在新式的Web應用程序中，HTML依舊在視圖中扮演著重要的角色，但一些新的技術

0x10軟考|網路工程師經驗分享之網路互聯與網際網路（四）

目錄 一、傳輸層協議TCP 二、傳輸層協議UDP 三、常見應用層協議 一、傳輸層協議TCP TCP協議：傳輸控制協議，面向位元組流按順序、連線、可靠、全雙工，可變滑動視窗、緩衝累積傳送。協議號6 下面是TCP段（斷頭），TCP頭（傳輸頭），TCP包

pandas縱向學習之10 minutes to pandas（四）

時間序列 resample函式的用法： In [14]: rng = pd.date_range('1/1/2012', periods=100, freq='S') In [15]: ts = pd.Series(np.random.randint(0, 500, len(rn

Logistic迴歸之梯度上升優化演算法（四）

Logistic迴歸之梯度上升優化演算法（四） 從疝氣病症狀預測病馬的死亡率 1、實戰背景 我們使用Logistic迴歸來預測患疝氣病的馬的存活問題。原始資料集點選這裡下載。資料中一個包含了368個樣本和28個特徵。這種病不一定源自馬的腸胃問題，其他問題也可能引發疝氣病。該資料集中包含了

深入理解java虛擬機器之自動記憶體管理機制（四）

記憶體分配與回收策略 （一）記憶體分配策略 　　　　給誰分配？分配到哪？是記憶體分配策略必須解答的問題。 　　　　java物件是分配的物件，往大方向來說，是分配到堆中，更細一點說，根據物件不同的特點分配到新生代和老年代區域。如果啟動了本地執行緒分配緩衝，就按執行緒優先在TLAB上分配。 　　　　一、新

View的工作原理之Measure過程原始碼學習（四）

       上一篇文章，學習了ViewGroup和View的measure流程。文章最後講到，本文將會學習ViewGroup和普通View的onMeasure方法的工作。        因為ViewGroup是

Unity5權威講解之菜鳥讀書筆記（四）

    Unity5權威講解之菜鳥讀書筆記（四） 16.Mecanim動畫系統 動畫型別 型別 特徵 Legacy Unity4.0

Qt網路程式設計之QNetworkRequest和QNetworkReply例項（四）

設想有如下場景：輸入若干的url，然後依次的下載並存儲到檔案。本案例使用QNetworkRequest和QNetworkReply。原始碼如下： 案例原始碼 標頭檔案 #pragma once //////////////////////////////////

【十】ArcGIS API for Javascript之專題圖的製作（四）熱力圖渲染（上）

一 、熱力圖定義 熱力圖（heat map）也稱熱圖，是以特殊顏色高亮區域的形式表示密度、溫度、氣壓、頻率等分佈的不易理解和表達的資料。 二、HeatmapRenderer esri/renderers/HeatmapRenderer類用來快速繪製熱力圖，將要

小白的JAVA之路——泛型講解（四）

由於我學習java的時候跳過了UI開發的知識學習，因此對於元件Compoent類會有點陌生，不過這並不影響我們講解泛型機制的原理，現在，讓我們來繼續學習泛型機制。 4.1 呼叫遺留程式碼 java中的遺留程式碼是指編寫於JAVA SE5.0之前的程式碼，一直遺留到現在。那

Python基礎-python資料型別之元祖、字典（四）

元祖　 　　Python的元組與列表類似，不同之處在於元組的元素不能修改。元組使用小括號，列表使用方括號。 tuple=(1,2,3,4) print(tuple) 　　訪問元祖 　　　　通過索引訪問，也可以進行切片操作 tuple=(1,2,3,4) print(tuple[2])

Linux學習之多執行緒程式設計（四）

言之者無罪，聞之者足以戒。 ——《詩序》 三、Linux執行緒的高階控制 1、一次性初始化 有些事需要且只能執行一次（比如互斥量初始化）。通常當初始化應用程式時，可以比較容易地將其放在main函式中。但當你寫一個庫函式時，就不能在main裡面初始化了，你可以用靜態初始化

程式設計菜鳥到大佬之路：計算機作業系統（四）

計算機系統概述 作業系統控制計算機 計算機系統操作方式 OS規定了合理操作計算機的工作流程。 OS的操作介面——系統程式 OS提供給使用者的功能級介面， 為使用者提供的解決操作計算機和計算共性問題的所有服務的集合。 OS的兩類作業級介面 離線

Android Broadcast原理分析之Android新版本限制（四）

目錄 概述 官方文件介紹 原始碼解析 適配 1. 概述 隨著Android版本不斷迭代，Android對後臺的管控越來越嚴格，對於APP而言，通常來講後臺活躍的主要是廣播以及service，而Google對於後臺的管控也著重就在這兩個元件上，本篇文章主要介紹

Linux之《荒島餘生》（四）I/O篇

我們在cpu篇就提到，iowait高一般代表硬碟到瓶頸了。wait的意思，就是等，就像等正在化妝的女朋友，總是帶著一絲焦躁。本篇是《荒島餘生》系列第四篇，I/O篇，計算機中最慢的那一環。其餘參見： Linux之《荒島餘生》（一）準備篇 Linux之《荒島餘生》（二）CPU篇 Linux之《荒島餘生》（三

各種音視訊編解碼學習詳解之 編解碼學習筆記（四）：Mpeg系列——Mpeg 4

   最近在研究音視訊編解碼這一塊兒，看到@bitbit大神寫的【各種音視訊編解碼學習詳解】這篇文章，非常感謝，佩服的五體投地。奈何大神這邊文章太長，在這裡我把它分解成很多小的篇幅，方便閱讀。大神部落格傳送門：https://www.cnblogs.com/skyofbitbit

《Linux系統》之"皮毛系列"（四） 使用者許可權管理

總有人問，Linux系統為什麼比windows系統相對安全呢？我們可以總結如下： （1）使用Linux系統的人數少，尤其在國內，很少有人關注Linux。 （2）因為Linux開源，任何的系統漏洞都會被民間高手，或者是官方人員很快的發現。從漏洞的發現到補丁的放出，時間相當短，沒有時間給病毒或者黑客