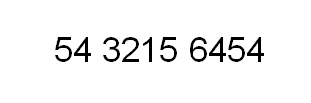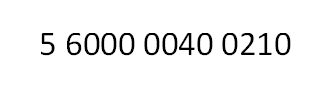【高精度】 利用分段儲存的方法儲存大數與運算
引:有時候我們遇到一種圖論題,就是要你將算出來的路徑中每條邊的權值之積或和求出來,雖然每條邊的權值都比較小,但算到最後結果卻很大,不得不用高精度方法儲存資料的時候,你怎麼處理?
傳統的高精度是用char[]陣列來儲存,這個對於上述問題,運算起來並不是很方便,這裡介紹一種基於分段進行資料儲存的大數處理方法給大家,其運算方便程度、空間和時間複雜度對比傳統的高精度演算法都有了一定提高。
=====================================================================
先介紹儲存機制,分段儲存的,這裡先隨便給個數,比如:5432156454
我們把這個數分成3段,每4位數作為一個段:
我們可以用三個變數來儲存這三段數
int first, seconed, thrid;
輸出時只需按thrid, seconed, first的順序把變數逐個輸出,就可以得到原來的大數了。
實際上我們可以把first, seconed, third合併成一個數組BigNumber[3] = {6454, 3215, 54},那麼分成3段的大數實際上是以數量級的形式被劃分成了3段,每個數量級之間的進製為10000,其中BigNumber[0]為該大數的第1數量級,這就是大數的基本儲存原理,其核心思想就是設定一個極大的進位制,然後按進位制分段存到數組裡。
--------------------------------------------
一個大數的儲存結構為:
#define SCALE ScaleNum //數量級之間的進位制,一般設成10的冪次方數
struct BigNumber{
int num[MAX]; //最高能儲存MAX個數量級位數的數
int oom; //該數的最高段儲存位置,可以看成是該數的資料規模
};
--------------------------------------------
我們分析一下儲存結構,可以發現能存的最大的數的位數為MAX* lg ScaleNum,而傳統的大數儲存的位數位MAX。
既然使用了這樣的儲存結構,那麼我們怎麼把一個數輸出?
其實很簡單,把BigNumber.num[]數組裡面的數從下標oom到0依次輸出即可,需要注意的地方就是除了最高段(BigNumber.num[oom]
有個數5600000400210,我們依舊以4位為一段將其分段,其數量級之間的進位制ScaleNum = 10000
存到BigNumber裡,其BigNumber.num[4] = {214, 40, 6000, 5}; BigNumber.oom = 4。
因為BigNumber.num[]是int陣列,每個段如果前面有0的話是會被捨去的,這時候直接輸出的話就只有5 6000 40 214,而不是5 6000 0040 0210。
我們看看要正確地輸出一個BigNumber型別的數,其函式該怎麼寫
#include <iostream>
#define SCALE 10000
struct BigNumber{
int num[100];
int oom;
};
int Bits(int x) //計算一個數有幾位,時間複雜度為O(lg ScaleNum)
{
if(x == 0) return 1;
int count = 1;
for(int i=10; i<=SCALE ;i*=10){
if(x/i == 0) return count;
count++;
}
}
void Print(BigNumber BigNum, int PrintBits = 4) //輸出大數BigNum,因為4位為1段,故每段應該打印出PrintBits = 4位數字
{
cout<<BigNum.num[BigNum.oom];//最高位可以直接輸出
int zero_fill; //計算在前面需要補幾個0的變數
for(int i=BigNum.oom-1; i>=0 ;i--){ //大迴圈,每次迴圈輸出一個段
zero_fill = PrintBits - Bits(BigNum.num[i]);//補0數量 = 應該列印的位數 - 當前段的數的位數
for(int count=0; count<zero_fill ;count++)//補0小迴圈
cout<<0;
cout<<BigNum.num[i];
}
cout<<endl;
}設大數的位數為N,Print()函式最外層時間複雜度為O(ooe),而求位數Bits()函式跟補0小迴圈的函式的時間複雜度都是O(lg ScaleNum)故整個輸出函式實際的時間複雜度為O(ooe*lg ScaleNum) 其中ooe = N/lg ScaleNum 故該輸出演算法時間複雜度為O(N)。
=====================================================================介紹完了大數的儲存機制跟輸出方法,大家也應該對這種演算法有一定的瞭解了,那麼我們談談怎麼用這種儲存結構進行加法以及乘法運算,引子裡提到過,這種儲存結構主要是為了方便大數與普通的int資料型別進行運算而創造的,所以接下來講的加法跟乘法,都是BigNumber + int 或 BigNumber * int的操作。
-----------------------------
先看加法
有一個int型別的數x,我們先分析一下加法的運算規則,5 6000 0040 0210 + 9999為例
我們依舊採取豎式計算,所以也是從最低段開始,一步一步往高的段進位。
程式碼很短很簡單,直接看就明白了。
#include <iostream>
#define SCALE 10000
BigNumber operator+ (int x)const
{
BigNumber R = *this;
int temp = x;
int pos = 0;
while(temp){
R.num[pos] += temp;
temp = R.num[pos] / SCALE;
R.num[pos++] %= SCALE;
}
/*數量級擴增判斷*/
if(pos > R.oom && R.num[pos]) R.oom = pos;
return R;
};豎式計算誰都懂,就不講下去了,上面圖片的兩個數怎麼通過程式碼所示的方法加起來,稍微認真點讀程式的話我想還是很容易想到的。。。
設大數的位數為N,加數的位數為M(M<= lg ScaleNum),則該演算法的時間複雜度為O(oom),而oom = N/ScaleNum,故實際時間複雜度為O(N/lg ScaleNum)
---------------------------------------------------
乘法計算
---
乘法計算的話這個儲存結構就用不著像傳統結構那樣也要豎式計算了,而是根據乘法分配律,將乘數x與被乘的大數BigNumber的每一個小段相乘,再從最低段開始一步一步向高的一段把數進位過來。
拿5 6000 0040 0210 * 9999做例子
實現的程式碼如下
BigNumber operator* (int x) const
{
BigNumber R = *this;
int last_carry = 0; //從前一位取得的進位
int now_carry; //當前位取得的進位
/*計算*/
for(int i=0; i<=R.oom ;i++){
now_carry = (R.num[i]*x+last_carry) / SCALE; //獲得進位
R.num[i] = (R.num[i]*x+last_carry) % SCALE;
last_carry = now_carry;
}
/*數量級擴增判斷*/
if(last_carry > 0){ //若最後的進位不為0,則擴增數量級
R.oom++;
R.num[R.oom] = last_carry;
}
return R;
};設大數的位數為N,乘數的位數為M,由於乘數不用進行資料型別轉換,所以這樣算時間複雜度與M無關,該演算法時間複雜度為O(oom),而oom = N/ScaleNum所以該演算法實際時間複雜度為O(N/ScaleNum),比起傳統的O(N*M)要好很多。
=====================================================================
以上便是該儲存結構下的大數加法與乘法運算,由於該儲存結構能直接跟int型別運算,所以在進行像階乘或者是路徑各權值之積這類需要一步一步疊加比較小的數最終結果為大數的運算時,有著比傳統高精度寫法寫法更簡便,時間複雜度更低的優點。與傳統高精度開同樣多的陣列,能存的資料的位數卻是傳統高精度儲存結構的lg ScaleNum倍,所以此寫法能表示的資料範圍更大,空間也更省。
=====================================================================
下面給一段程式碼,其功能是計算n的階乘,輸出,然後將其結果加上9999,再輸出
#include <iostream>
#include <cstring>
#define SCALE 10000
using namespace std;
struct BigNumber{
int num[100];
int oom;
BigNumber operator+ (int x)const
{
BigNumber R = *this;
int temp = x;
int pos = 0;
while(temp){
R.num[pos] += temp;
temp = R.num[pos] / SCALE;
R.num[pos++] %= SCALE;
}
/*數量級擴增判斷*/
if(pos > R.oom && R.num[pos]) R.oom = pos;
return R;
};
BigNumber operator* (int x) const
{
BigNumber R = *this;
int last_carry = 0; //從前一位取得的進位
int now_carry; //當前位取得的進位
/*計算*/
for(int i=0; i<=R.oom ;i++){
now_carry = (R.num[i]*x+last_carry) / SCALE; //獲得進位
R.num[i] = (R.num[i]*x+last_carry) % SCALE;
last_carry = now_carry;
}
/*數量級擴增判斷*/
if(last_carry > 0){ //若最後的進位不為0,則擴增數量級
R.oom++;
R.num[R.oom] = last_carry;
}
return R;
};
};
int Bits(int x) //計算一個數有幾位,時間複雜度為O(lgScaleNum)
{
if(x == 0) return 1;
int count = 1;
for(int i=10; i<=SCALE ;i*=10){
if(x/i == 0) return count;
count++;
}
}
void Print(BigNumber BigNum, int PrintBits = 4) //輸出大數BigNum,因為4位為1段,故每段應該打印出PrintBits = 4位數字
{
cout<<BigNum.num[BigNum.oom];//最高位可以直接輸出
int zero_fill; //計算在前面需要補幾個0的變數
for(int i=BigNum.oom-1; i>=0 ;i--){ //大迴圈,每次迴圈輸出一個段
zero_fill = PrintBits - Bits(BigNum.num[i]);//補0數量 = 應該列印的位數 - 當前段的數的位數
for(int count=0; count<zero_fill ;count++)//補0小迴圈
cout<<0;
cout<<BigNum.num[i];
}
cout<<endl;
}
int main()
{
BigNumber big_num;
big_num.oom = 0;
memset(big_num.num, 0, sizeof(big_num.num));
/*算n的階乘*/
int n;
cin>>n;
big_num.num[0] = 1;
for(int i=n; i>=1; i--)
big_num = big_num * i;
Print(big_num);
/*之後加上9999*/
big_num = big_num + 9999;
Print(big_num);
return 0;
}