這兩天在看樹的部分，先總結一下二叉樹。

什麼是樹？

樹也是一種資料結構，是由n個結點組成的具有層次關係的集合。樹由根結點和子節點組成，與現實生活中的樹不同，這裡的樹，根結點是在最上面的，葉子結點在下面，就像是將現實中的樹倒著掛起來一樣。

樹的特點：

• 每個結點有零個或多個子結點。
• 每一個子結點只有一個父結點。
• 沒有前驅的結點稱為根結點，沒有子結點的結點為葉子結點。
• 除根結點外，每個子結點可分為m個不相交的子樹。

什麼是二叉樹？

二叉樹特點是每個結點最多有兩個子結點。

樹和二叉樹的區別:

• 樹中的結點個數至少為1，而二叉樹中的結點個數可以為0；
• 樹中結點的度沒有限制，而二叉樹中結點的最大度為2.

二叉樹的實現:

這裡二叉樹的建立時採用遞迴的方式，並且每次建立的都是根節點，採用的是前序遍歷的方式。

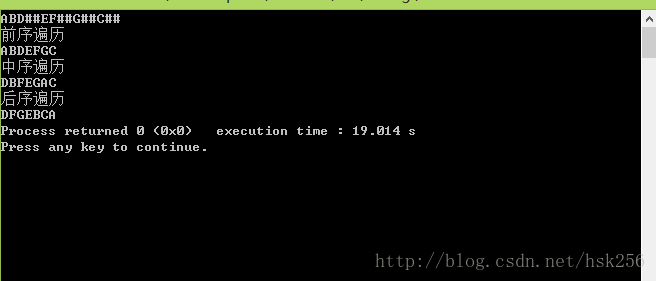
<span style="font-size:18px;">#include <stdio.h>
#include <stdlib.h>
typedef char TElemType;
typedef struct BiNode {
    TElemType data;
    struct BiNode *lchild,*rchild;
}BiNode,*BiTree;

//建立二叉樹
BiTree createBiTree(BiTree *T) {
    TElemType ch;
    scanf("%c",&ch);
    if(ch=='#') {
        *T = NULL;
    }else {
        *T = (BiTree)malloc(sizeof(BiNode));
        if(!*T)
            exit(-1);

         (*T)->data = ch;
        createBiTree(&(*T)->lchild);
        createBiTree(&(*T)->rchild);
    }
    return T;
}

//前序遍歷
void preorderTraverse(BiTree T) {
    if(T==NULL)
        return;
    printf("%c",T->data);
    preorderTraverse(T->lchild);
    preorderTraverse(T->rchild);
}

//中序遍歷
void InorderTraverse(BiTree T) {
   if(T){
    InorderTraverse(T->lchild);
    printf("%c",T->data);
    InorderTraverse(T->rchild);
   }
}

//後序遍歷
void PostorderTraverse(BiTree T) {
    if(T) {
        PostorderTraverse(T->lchild);
        PostorderTraverse(T->rchild);
        printf("%c",T->data);
    }
}
int main()
{
    BiTree t;
    createBiTree(&t);
    printf("%s\n","前序遍歷");
    preorderTraverse(t);
    printf("\n");
    printf("%s","中序遍歷");
    printf("\n");
    InorderTraverse(t);
    printf("\n");
    printf("%s\n","後序遍歷");
    PostorderTraverse(t);

    return 0;
}
</span>