洛谷 P2827 蚯蚓
題目描述
本題中,我們將用符號[c]表示對c向下取整,例如:[3.0」= [3.1」=[3.9」=3。
蛐蛐國最近蚯蚓成災了!隔壁跳蚤國的跳蚤也拿蚯蚓們沒辦法,蛐蛐國王只好去請神刀手來幫他們消滅蚯蚓。
蛐蛐國裡現在共有n只蚯蚓(n為正整數)。每隻蚯蚓擁有長度,我們設第i只蚯蚓的長度為a_i(i=1,2,...,n),並保證所有的長度都是非負整數(即:可能存在長度為0的蚯蚓)。
每一秒,神刀手會在所有的蚯蚓中,準確地找到最長的那一隻(如有多個則任選一個)將其切成兩半。神刀手切開蚯蚓的位置由常數p(是滿足0<p<1的有理數)決定,設這隻蚯蚓長度為x,神刀手會將其切成兩隻長度分別為[px]和x-[px]的蚯蚓。特殊地,如果這兩個數的其中一個等於0,則這個長度為0的蚯蚓也會被保留。此外,除了剛剛產生的兩隻新蚯蚓,其餘蚯蚓的長度都會增加q(是一個非負整常數)。
蛐蛐國王知道這樣不是長久之計,因為蚯蚓不僅會越來越多,還會越來越長。蛐蛐國王決定求助於一位有著洪荒之力的神祕人物,但是救兵還需要m秒才能到來......
(m為非負整數)
蛐蛐國王希望知道這m秒內的戰況。具體來說,他希望知道:
•m秒內,每一秒被切斷的蚯蚓被切斷前的長度(有m個數)
•m秒後,所有蚯蚓的長度(有n+m個數)。
蛐蛐國王當然知道怎麼做啦!但是他想考考你......
輸入輸出格式
輸入格式:第一行包含六個整數n,m,q,u,v,t,其中:n,m,q的意義見【問題描述】;u,v,t均為正整數;你需要自己計算p=u/v(保證0<u<v)t是輸出引數,其含義將會在【輸出格式】中解釋。
第二行包含n個非負整數,為ai,a2,...,an,即初始時n只蚯蚓的長度。
同一行中相鄰的兩個數之間,恰好用一個空格隔開。
保證1<=n<=10^5,0<m<7*10^6,0<u<v<10^9,0<=q<=200,1<t<71,0<ai<10^8。
輸出格式:第一行輸出[m/t]個整數,按時間順序,依次輸出第t秒,第2t秒,第3t秒……被切斷蚯蚓(在被切斷前)的長度。
第二行輸出[(n+m)/t]個整數,輸出m秒後蚯蚓的長度;需要按從大到小的順序,依次輸出排名第t,第2t,第3t……的長度。
同一行中相鄰的兩個數之間,恰好用一個空格隔開。即使某一行沒有任何數需要 輸出,你也應輸出一個空行。
請閱讀樣例來更好地理解這個格式。
【資料範圍】
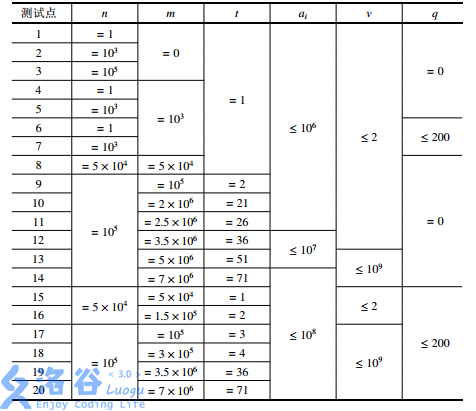
輸入輸出樣例
輸入樣例#1:3 7 1 1 3 1 3 3 2輸出樣例#1:
3 4 4 4 5 5 6 6 6 6 5 5 4 4 3 2 2輸入樣例#2:
3 7 1 1 3 2 3 3 2輸出樣例#2:
4 4 5 6 5 4 3 2輸入樣例#3:
3 7 1 1 3 9 3 3 2輸出樣例#3:
//空行 2
說明
【樣例解釋1】
在神刀手到來前:3只蚯蚓的長度為3,3,2。
1秒後:一隻長度為3的蚯蚓被切成了兩隻長度分別為1和2的蚯蚓,其餘蚯蚓的長度增加了1。最終4只蚯蚓的長度分別為(1,2),4,3。括號表示這個位置剛剛有一隻蚯蚓被切斷
2秒後:一隻長度為4的蚯蚓被切成了1和3。5只蚯蚓的長度分別為:2,3,(1,3),4。
3秒後:一隻長度為4的蚯蚓被切斷。6只蚯蚓的長度分別為:3,4,2,4,(1,3)。
4秒後:一隻長度為4的蚯蚓被切斷。7只蚯蚓的長度分別為:4,(1,3),3,5,2,4。
5秒後:一隻長度為5的蚯蚓被切斷。8只蚯蚓的長度分別為:5,2,4,4,(1,4),3,5。
6秒後:一隻長度為5的蚯蚓被切斷。9只蚯蚓的長度分別為:(1,4),3,5,5,2,5,4,6。
7秒後:一隻長度為6的蚯蚓被切斷。10只蚯蚓的長度分別為:2,5,4,6,6,3,6,5,(2,4)。所以,7秒內被切斷的蚯蚓的長度依次為3,4,4,4,5,5,6。7秒後,所有蚯蚓長度從大到小排序為6,6,6,5,5,4,4,3,2,2
【樣例解釋2】
這個資料中只有t=2與上個數據不同。只需在每行都改為每兩個數輸出一個數即可。
雖然第一行最後有一個6沒有被輸出,但是第二行仍然要重新從第二個數再開始輸出。
【樣例解釋3】
這個資料中只有t=9與上個數據不同。
注意第一行沒有數要輸出,但也要輸出一個空行。
【分析】
【程式碼】
//NOIP 2016 蚯蚓
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#define inf 2e9+7
#define ll long long
#define M(a) memset(a,0,sizeof a)
#define fo(i,j,k) for(i=j;i<=k;i++)
using namespace std;
const int mxn=7000005;
int q1[mxn],q2[mxn],q3[mxn];
int h1,t1,h2,t2,h3,t3;
int n,m,q,u,v,t;
inline bool comp(int x,int y)
{
return x>y;
}
int main()
{
int i,j;
scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t);
fo(i,1,n) scanf("%d",&q1[i]);
sort(q1+1,q1+n+1,comp);
h1=h2=h3=1,t1=n;
fo(i,1,m)
{
int now=-inf;
if(h1<=t1) now=max(now,q1[h1]);
if(h2<=t2) now=max(now,q2[h2]);
if(h3<=t3) now=max(now,q3[h3]);
if(now==q1[h1] && h1<=t1) h1++;
else if(now==q2[h2] && h2<=t2) h2++;
else if(now==q3[h3] && h3<=t3) h3++;
now+=q*(i-1);
if(i%t==0) printf("%d ",now);
ll L=(ll)now*u/v,S=now-L;
if(L<S) swap(L,S);
q2[++t2]=L-q*i,q3[++t3]=S-q*i;
}
printf("\n");
fo(i,1,n+m)
{
int now=-inf;
if(h1<=t1) now=max(now,q1[h1]);
if(h2<=t2) now=max(now,q2[h2]);
if(h3<=t3) now=max(now,q3[h3]);
if(now==q1[h1] && h1<=t1) h1++;
else if(now==q2[h2] && h2<=t2) h2++;
else if(now==q3[h3] && h3<=t3) h3++;
now+=q*m;
if(i%t==0) printf("%d ",now);
}
printf("\n");
return 0;
}