java 實現跳躍表
跳躍連結串列是一種隨機化資料結構,基於並聯的連結串列,其效率可比擬於二叉查詢樹(對於大多數操作需要O(log n)平均時間),並且對併發演算法友好。
基本上,跳躍列表是對有序的連結串列增加上附加的前進連結,增加是以隨機化的方式進行的,所以在列表中的查詢可以快速的跳過部分列表(因此得名)。所有操作都以對數隨機化的時間進行。
實現原理:
跳躍表的結構是:假如底層有10個節點, 那麼底層的上一層理論上就有5個節點,再上一層理論上就有2個或3個節點,再上一層理論上就有1個節點。所以從這裡可以看出每一層的節點個數為其下一層的1/2個元素,以此類推。從這裡我們可以看到,從插入時我們只要保證上一層的元素個數為下一層元素個數的
程式碼結構:
節點類:
String key 鍵值 對跳躍表的操作都是根據鍵值進行的
Int value 實際值
Node up,down,left,right; 每個節點都有四個方向
String tou;
String wei; 每層連結串列的頭和尾節點
跳躍表類:
Head 頭節點
Tail 尾結點
H 層數
Size 元素個數
Random 隨機數,用來確定需不需要增加層數 即:擲硬幣
findF () 按從小到大的順序找到應該插入的位置 插入排序法
Add () 新增節點函式,在最底層插入結點後,進行擲硬幣來確定是否需要曾增加層數,直到擲硬幣不能增加層數為止,增加層數的同事需要把增加之後的節點進行連線。
Find() 根據跳躍表進行查詢並列印路線。查詢從最上層開始然後找到被查詢節點的前個節點小於被查詢節點,然後被查詢節點的後一個節點大於其被查詢節點,則從被查詢節點的前一個節點向下走
引用:http://www.java123.net/936905.html
1.
跳躍表的引入
1.
我們知道,普通單鏈表查詢一個元素的時間複雜度為O(n),即使該單鏈表是有序的,我們也不能通過2分的方式縮減時間複雜度。

如上圖,我們要查詢元素為55的結點,必須從頭結點,迴圈遍歷到最後一個節點,不算-INF(負無窮)一共查詢8次。那麼用什麼辦法能夠用更少的次數訪問55呢?最直觀的,當然是新開闢一條捷徑去訪問55。
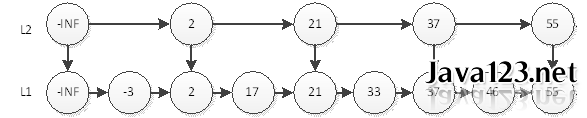
如上圖,我們要查詢元素為55的結點,只需要在L2層查詢4次即可。在這個結構中,查詢結點為46的元素將耗費最多的查詢次數5次。即先在L2查詢46,查詢4次後找到元素55,因為連結串列是有序的,46一定在55的左邊,所以L2層沒有元素46。然後我們退回到元素37,到它的下一層即L1層繼續搜尋46。非常幸運,我們只需要再查詢1次就能找到46。這樣一共耗費5次查詢。
那麼,如何才能更快的搜尋55呢?有了上面的經驗,我們就很容易想到,再開闢一條捷徑。
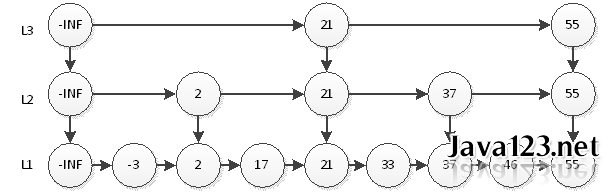
如上圖,我們搜尋55只需要2次查詢即可。這個結構中,查詢元素46仍然是最耗時的,需要查詢5次。即首先在L3層查詢2次,然後在L2層查詢2次,最後在L1層查詢1次,共5次。很顯然,這種思想和2分非常相似,那麼我們最後的結構圖就應該如下圖。
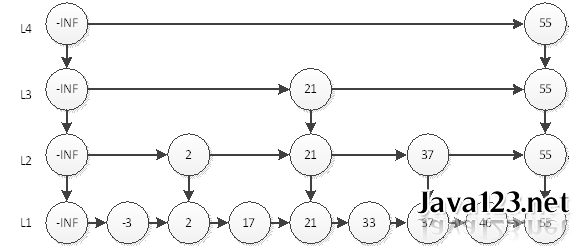
我們可以看到,最耗時的訪問46需要6次查詢。即L4訪問55,L3訪問21、55,L2訪問37、55,L1訪問46。我們直覺上認為,這樣的結構會讓查詢有序連結串列的某個元素更快。那麼究竟演算法複雜度是多少呢?
如果有n個元素,因為是2分,所以層數就應該是log n層 (本文所有log都是以2為底),再加上自身的1層。以上圖為例,如果是4個元素,那麼分層為L3和L4,再加上本身的L2,一共3層;如果是8個元素,那麼就是3+1層。最耗時間的查詢自然是訪問所有層數,耗時logn+logn,即2logn。為什麼是2倍的logn呢?我們以上圖中的46為例,查詢到46要訪問所有的分層,每個分層都要訪問2個元素,中間元素和最後一個元素。所以時間複雜度為O(logn)。
至此為止,我們引入了最理想的跳躍表,但是如果想要在上圖中插入或者刪除一個元素呢?比如我們要插入一個元素22、23、24……,自然在L1層,我們將這些元素插入在元素21後,那麼L2層,L3層呢?我們是不是要考慮插入後怎樣調整連線,才能維持這個理想的跳躍表結構。我們知道,平衡二叉樹的調整是一件令人頭痛的事情,左旋右旋左右旋……一般人還真記不住,而調整一個理想的跳躍表將是一個比調整平衡二叉樹還複雜的操作。幸運的是,我們並不需要通過複雜的操作調整連線來維護這樣完美的跳躍表。有一種基於概率統計的插入演算法,也能得到時間複雜度為O(logn)的查詢效率,這種跳躍表才是我們真正要實現的。
容易實現的跳躍表
1.
容易實現的跳躍表,它允許簡單的插入和刪除元素,並提供O(logn)的查詢時間複雜度,以下我們簡稱為跳躍表。
先討論插入,我們先看理想的跳躍表結構,L2層的元素個數是L1層元素個數的1/2,L3層的元素個數是L2層的元素個數的1/2,以此類推。從這裡,我們可以想到,只要在插入時儘量保證上一層的元素個數是下一層元素的1/2,我們的跳躍表就能成為理想的跳躍表。那麼怎麼樣才能在插入時保證上一層元素個數是下一層元素個數的1/2呢?很簡單,拋硬幣就能解決了!假設元素X要插入跳躍表,很顯然,L1層肯定要插入X。那麼L2層要不要插入X呢?我們希望上層元素個數是下層元素個數的1/2,所以我們有1/2的概率希望X插入L2層,那麼拋一下硬幣吧,正面就插入,反面就不插入。那麼L3到底要不要插入X呢?相對於L2層,我們還是希望1/2的概率插入,那麼繼續拋硬幣吧!以此類推,元素X插入第n層的概率是(1/2)的n次。這樣,我們能在跳躍表中插入一個元素了。
程式碼:
package 跳躍表;
import java.util.*;
public class SkipList {
public Node head; //頭節點
public Node tail; //尾結點
public int h; //層數
public int size; //元素個數
public Random rand; //每次的隨機數用來確定需不需要增加層數
public SkipList(){
Node p1 = new Node(Node.tou,0);
Node p2 = new Node(Node.wei, 0);
head=p1;
tail=p2;
head.setRight(tail);
tail.setLeft(head);
h=0;
size=0;
rand = new Random();
}
public boolean isEmpty(){
if(size==0){
return true;
}
return false;
}
//找到需要插入位置的前一個節點
public Node findF(String k){
Node temp;
temp=head;
while(true){
while(temp.getRight().key!=Node.wei&&temp.getRight().key.compareTo(k)<=0){
/*
* 當連結串列最底層不為空的時候,從當前層向尾部方向開始查詢,直到查詢temp.getRight的下一個值大於 當前k的值為止,此時temp小於或等於當前k的值
* 要插入的位置即為temp之後的位置了
*/
temp=temp.getRight();
}
if(temp.getDown()!=null){
temp=temp.getDown();
}else{
break;
}
}
return temp; //找到節點並返回
}
public int add(String k, int v){
Node temp, temp1;
temp=findF(k);
int i; //當前層數
if(k.equals(temp.getKey())){
System.out.println("物件屬性完全相同無法新增!");
int a=temp.value;
temp.value=v;
return a;
}
temp1=new Node(k,v);
temp1.setLeft(temp);
temp1.setRight(temp.getRight());
temp.getRight().setLeft(temp1);
temp.setRight(temp1);
i=0;
while(rand.nextDouble()<0.5){ //進行隨機,是否需要 在上層新增
if(i>=h){ //若當前層數超出了高度,則需要另建一層
Node p1 ,p2 ;
h=h+1;
p1=new Node(Node.tou,0);
p2=new Node(Node.wei,0);
p1.setRight(p2);
p1.setDown(head);
p2.setLeft(p1);
p2.setDown(tail);
head.setUp(p1);
tail.setUp(p2);
head=p1;
tail=p2;
}
while(temp.getUp() == null){
temp=temp.getLeft();
}
temp=temp.getUp();
Node node=new Node(k,v);
node.setLeft(temp);
node.setRight(temp.getRight());
node.setDown(temp1);
temp.getRight().setLeft(node);
temp.setRight(node);
temp1.setUp(node);
temp1=node;
i=i+1;
}
size=size+1;
return 0;
}
//節點查詢
public Node find(String k){
Node temp=head;
Node node;
node=temp;
System.out.println("查詢路線"); //用於測試
while(temp!=null){
while(node.getRight().key!=Node.wei&&node.getRight().getKey().compareTo(k)<=0){//&&node.getRight().getValue()!=v
node=node.getRight();
System.out.print("--->"+node.getKey());
}
if(node.getDown()!=null){
node=node.getDown();
System.out.print("--->"+node.getKey());
}else{
if(node.key.equals(k)){//&&node.getRight().value==v
//node.setValue(111111111); //修改
System.out.println("--->"+node.getKey());
System.out.print("--->"+node.getValue());
return node;
}
return null;
}
}
return null;
}
//節點刪除
public void delNode(String k){ //呼叫查詢函式,刪除最底層的某個節點,並把其節點的左右相連,和連結串列操作一樣,只是其上方若有則都需要調整
Node temp=find(k);
while(temp!=null){
temp.getLeft().setRight(temp.getRight());
temp.getRight().setLeft(temp.getLeft());
temp=temp.getUp();
}
}
public void print(){
Node node;
Node node1=head;
while(node1!=null){
int k=0;
node=node1;
while(node!=null){
System.out.print(node.getKey()+"\t");
k++;
node=node.getRight();
}
System.out.print("\t");
System.out.print("("+k+")");
//System.out.print(node.getKey());
System.out.println();
//node=node1.getDown();
node1=node1.getDown();
}
}
}
class Node{
public String key;
public int value;
public Node up, down,left , right;
public static String tou=new String("--頭--");
public static String wei=new String("--尾--");
public Node(String k, int v){
this.key=k;
this.value=v;
up=down=left=right=null;
}
public void setUp(Node up){
this.up=up;
}
public Node getUp(){
return up;
}
public void setDown(Node down){
this.down=down;
}
public Node getDown(){
return down;
}
public void setLeft(Node left){
this.left=left;
}
public Node getLeft(){
return left;
}
public void setRight(Node right){
this.right=right;
}
public Node getRight(){
return right;
}
public void setKey(String k){
this.key=k;
}
public String getKey(){
return key;
}
public void setValue(int v){
this.value=v;
}
public int getValue(){
return value;
}
}
package 跳躍表;
public class Test {
public static void main(String[] args){
SkipList s = new SkipList();
// s.add("AAA", 122);
int i=0;
for(;i<30;i++){ //隨機數字進行測試
s.add(String.valueOf(i), i);
}
s.print();
System.out.println("\n\n----------\n\n\n");
if(s.find("22")!=null){ //查詢
System.out.println("\nOK");
}else{//找不到
System.out.println("\nfalse");
}
s.delNode("0"); //刪除
s.print();
}
}
測試結果:
