基於Cuda的幾種並行稀疏矩陣乘法方法(一)
最近由於研究需要和興趣看了很多稀疏矩陣乘法的演算法,這方面的研究千奇百怪,研究人員真的是十八般武藝全都用上了,好吧,就讓我來說說這個東西吧,由於這個東西實在方法太多,所以請容許我一節一節地去完善。
1、儲存方式
稀疏矩陣的儲存方式真的非常多,也各有千秋,它們包括CSR(許多庫的首選儲存方式),COO(MATLAB儲存稀疏矩陣的方式),CSC(這個也可以看成是CSR,做個轉置就完了),ELL等等。最近還看到了一種aligned-COO的儲存方式。雖然有那麼多種儲存方式,但思想都是接近的,比如說CSR吧,就是隻儲存非零元素val,然後把列標都記錄下來col_ptr,行標取每行第一個數在val中的位置。就不舉例子了,網上說得很全。
2、CUDA並行的計算方法
其實CUDA最重要的事情有兩個方面,一個是對全域性記憶體的訪問,另一個是所有執行緒的divergence的問題。所以儲存結構和實現方法是相當重要的,我首先講兩個最簡單的基於CSR儲存的實現方法,一種是利用每個block算一列,另一種是利用每個block算一行。
其實這倆方法都挺簡單,沒有做任何優化的話還是直接貼程式碼吧,等我想想優化怎麼寫再詳細說說:
每個block計算一列:
while (row<M)
{
index_start=row_ptr[row];index_end=row_ptr[row+1];
sum=0;
for (int k=index_start;k<index_end;k++)
{
col_index=col_ptr[k];
a_r=col_index/M_B;b_r=col_index%M_B;
a=A[a_r*N_A+a_c];b=B[b_r*N_B+b_c];
khro_value 每個block計算一行:
while (j<N)
{
sum=0;
for (int k=0;k<num_part_row;k++)
{
if((k+t)>nnz_row)
{
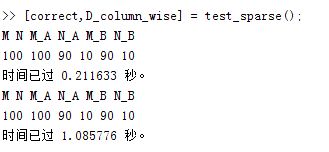
break 3、實驗結果
其實挺好分析的,如果每個block計算一個列的話,有很嚴重的divergence的問題還有資料訪問的問題,也就是說uncoalesced.但是如果每個block計算一行的話,上面的問題就可以比較好解決。但是我的實驗裡面為啥用了shared_memory卻不如沒有用shared_memory好呢,這個我還沒有想得很清楚。。。還是貼張實驗圖片吧,確實這個uncoalesced的影響還是很大的。