中國剩餘定理（CRT）的表述如下

設正整數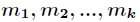兩兩互素，則同餘方程組

有整數解。並且在模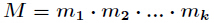下的解是唯一的，解為

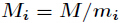
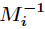
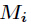
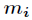
其中，而為模的逆元。

具體證明如下：

找出所有整數x,使其被3，5和7除時，餘數分別為2，3和2

x≡2(mod 3)

x≡3(mod 5)=>x = △ + 3*5*7*t(△為期中的一個解，t為整數）

x≡2(mod 7)

在同餘中最重要的觀念就是求出第一個解，那麼x = △ + 3*5*7*t就是通解。那怎麼求一個解呢？

利用同餘的加性：

把x拆成a+b+c,即x = a + b + c

令

a≡2(mod 3)

a≡0(mod 5)=>a=35p(可以看到p取1的時候滿足a≡2(mod3),即a=35)

a≡0(mod 7)

接下來要求b：

b≡0(mod 3)

b≡3(mod 5)=>b=21q(可以看到q取3的時候滿足b≡3(mod5),即b=63)

b≡0(mod 7)

求c

c≡0(mod 3)

c≡0(mod 5)=>c=15m(可以看到m取2的時候滿足c≡2(mod7),即c=30)

c≡2(mod 7)

得

x≡2(mod 3)  ≡ a + b + c

x≡3(mod 5)  ≡ a + b + c

x≡2(mod 7)  ≡ a + b + c

a b  c 都求出來之後，可以利用同餘的加性

x = a + b + c = 128是一個解，x = 128 + 105t 在適當調整t之後就可以求出x在任何範圍內的解，比如說求最小正整數解，這時候t取-1，得x=23

利用同餘的乘性：

之前令x = a + b + c,用同餘的乘性之後x = 2*a' + 3*b' + 2*c'

a'≡1(mod 3) 

a'≡0(mod 5)=>a'=35p(可以看到p取2的時候滿足a'≡1(mod3),即a'=70)

a'≡0(mod 7)

接下來要求b'：

b'≡0(mod 3)

b'≡1(mod 5)=>b'=21q(可以看到q取1的時候滿足b'≡1(mod5),即b'=21)

b'≡0(mod 7)

現在來看c'

c'≡0(mod 3)

c'≡0(mod 5)=>c'=15m(可以看到m取1的時候滿足c'≡1(mod7),即c'=15)

c'≡1(mod 7)

代入a' b' c'之後就可以得到x的一個解及其通解

x = 2*70 + 3*21 +2*15 

x = 233 + 105t

在知道同餘的加性和乘性之後再看下面這個公式就沒有什麼問題了

最後分享YouTube上關於同餘加性和乘性的講解連結